A sphere of mass m held at a height 2R between a wedge of same m and a rigid wall, is released from, Assuming that all the surfaces are frictionless. Find the speed of the bodies when the sphere hits the ground.
 .
.
If speed of sphere is v downwards then speed of wedge at this instant will be v cot α in horizontal direction.
Now,
Decrease in potention energy of sphere=increase in kinetic energy of both
∴mgR=12mv2+12(vcosα)2
=12mv2α
∴v=√2gRsinα=speed of sphere
and speed of wedge =vcotα
=√2gRcosα.
Similar Questions
A block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
View SolutionThe system shown in fig. is given an acceleration a towards left. Assuming all the surfaces to be frictionless, find the normal reactions applied by wedge on the sphere.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 1 kg is released from the top of a wedge of mass 2 kg. Height of wedge is 10 meter and all the surfaces are frictionless. Then
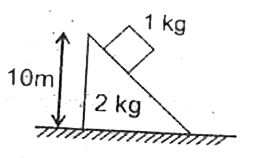 ADisplacement of centre of mass of system in vertical direction is zero.BDisplacement of centre of mass of system, vertically downwards, is 103m,CRation of normal reaction between block and wedge to the acceleration of wedge w.r.t ground is 4 (in kg).DMomentum of system will not be conserved in horizontal direction.
ADisplacement of centre of mass of system in vertical direction is zero.BDisplacement of centre of mass of system, vertically downwards, is 103m,CRation of normal reaction between block and wedge to the acceleration of wedge w.r.t ground is 4 (in kg).DMomentum of system will not be conserved in horizontal direction. - Question 2 - Select One
A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
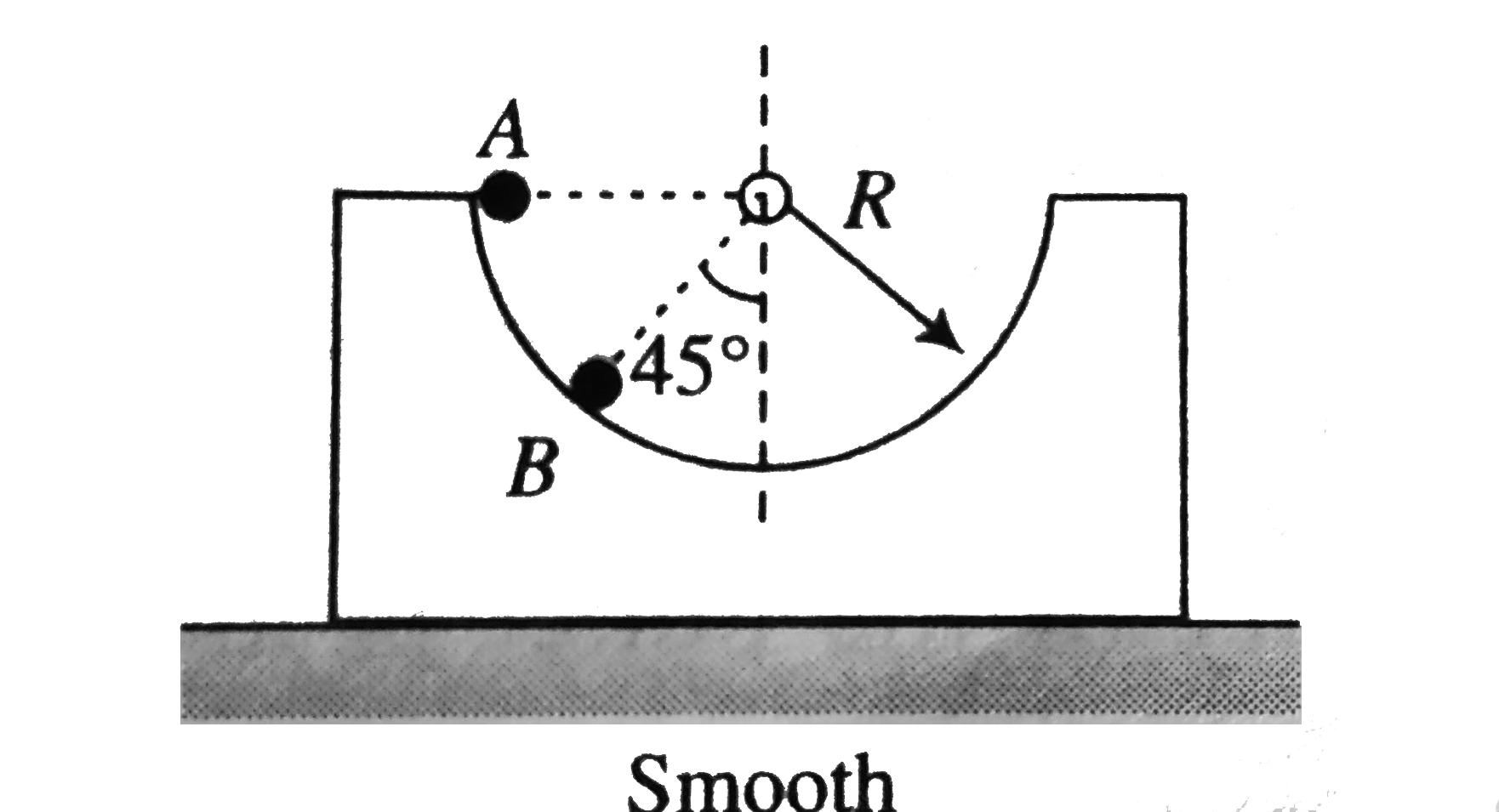 A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gR
A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gR - Question 3 - Select One
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
(a) In the arrangmenet shown in the figure the frictional coefficient between the traingular wedge and floor is μ=1/√3. The frictional force is sufficient to keep the system in equilibrium.
Find how much the normal reaction between the wedge and floor is displaced from the centre of mass of wedge. All other surface are frictionless. Assume masses of both the bodies same and equal to m. Radius of sphere =R, length of side of triangular wedge d =3√3R.
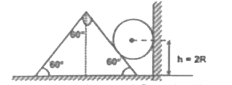
( b) If the surface of contact between the floor & the wedge also becomes frictionless, the find the speed of both bodies when sphere hits the ground. Initial height of centre of mass of sphere = 2R as shown.View SolutionIn the arrangement shown in figure, the rod of mass mhelp by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 View Solution
View SolutionTwo smooth wedges of equal mass m are placed as shown in figure. All surfaces are smooth. Find the velocities of A & B when A hits the ground.
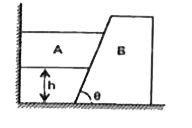 View Solution
View SolutionA body is released from the top of a tower of height 50 m. Find the velocity with which the body hits the ground. (g=9.8m/s2)
View SolutionA wedge of mass M lies on a smooth fixed wedge of inclination θ. A particle of mass m lies on the wedge of mass M in the figure. All surfaces are frictionless and the distance of the block from the fixed wedge is l. Find.
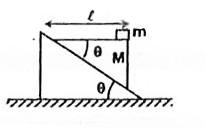
(a) Normal reaction between m and M
(b) the time after which the particle will hit the fixed plane.View Solution

