System shown in figure is in equilibrium, find the magnitude of net change in the string tension between two masses just after, when one of the springs in cut, Mass of both the blocks is same and equal to m spring constant of both springs is k.
 .
.
mg2
mg4
mg3
3mg2
The correct Answer is:A
Ti=gh......(i)
2kx=2mg
∴kx=mg
One kx force (acting is upward directon) is suddenly removed. So, net downward force on system will be kx or mg. Threrfore, net downward acceleration of system,
a=mg2m=g2
Free body diagram of lower block gives the equation,
mg−Tf=ma=mg2
∴Tf=mg2
From these two equation, we get
ΔT=mg2.
Similar Questions
The system shown in the Fig. is in equilibrium. Find the initial acceleration of A, B and C just after the spring 2 is cut.
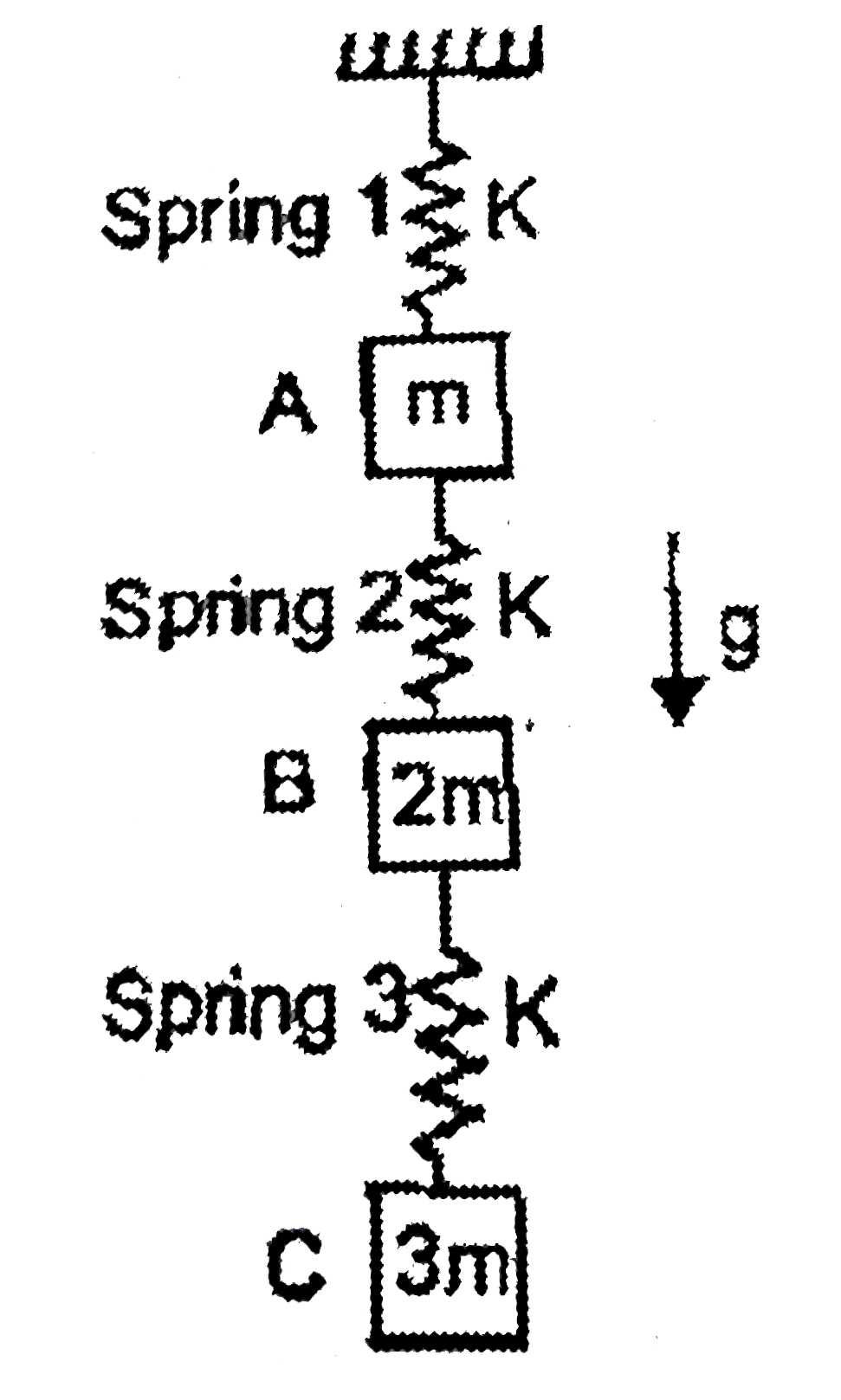 View Solution
View SolutionThe system shown in the figure is in equilibrium and all the blocks are at rest. Assume that the masses of the strings, the pulley and the spring and negligible with respect to the masses of the blocks and friction is absent. Find the acceleration of block C, just after cutting the spring 1. [g=10ms−2]
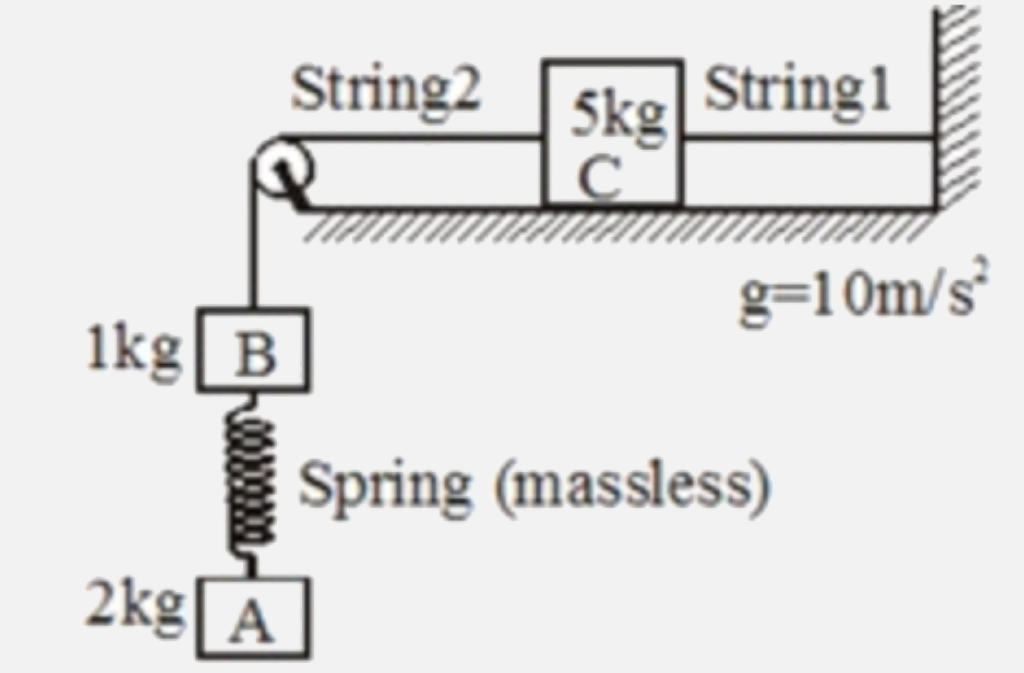 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
System shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:
 Ag/2 upwards, g downwardsBg upwards, g/2 downwardsCg upwards, 2g downwardsD2g upwards, g downwards
Ag/2 upwards, g downwardsBg upwards, g/2 downwardsCg upwards, 2g downwardsD2g upwards, g downwards - Question 2 - Select One or More
System shown in figure is equilibrium in vertical plane. Consider the string and spring to be massless. Both the blocks have same mass 'm'. If the string is cut, then just after cutting it :
 AAcceleration of 'A' is 'g' upwardsBAcceleration of 'A' is '2g' upwardsCAcceleration of 'B' is 'g' upwardsDAcceleration of 'B' is 'g' downwards
AAcceleration of 'A' is 'g' upwardsBAcceleration of 'A' is '2g' upwardsCAcceleration of 'B' is 'g' upwardsDAcceleration of 'B' is 'g' downwards - Question 3 - Select One
A block of mass 1kg is dropped on a spring - mass system as shown in the figure. The block traves 100 meters in the air before strinking the 3 kg mass. Calculate maximum compression in the spring, if both the blocks move together after the collision. Spring constant of the string k=1.25×106.
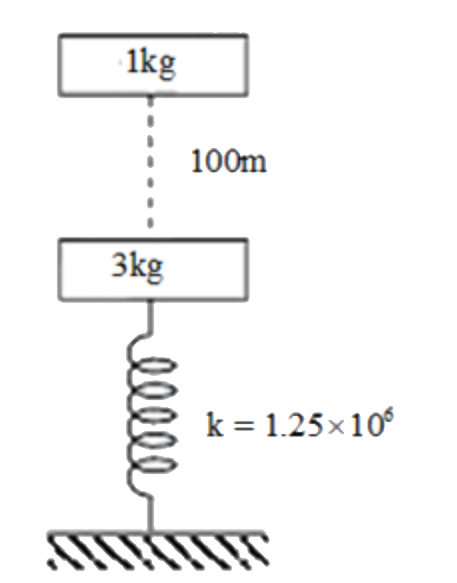 A2 cmB4 cmC8 cmD16 cm
A2 cmB4 cmC8 cmD16 cm
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.
 View Solution
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
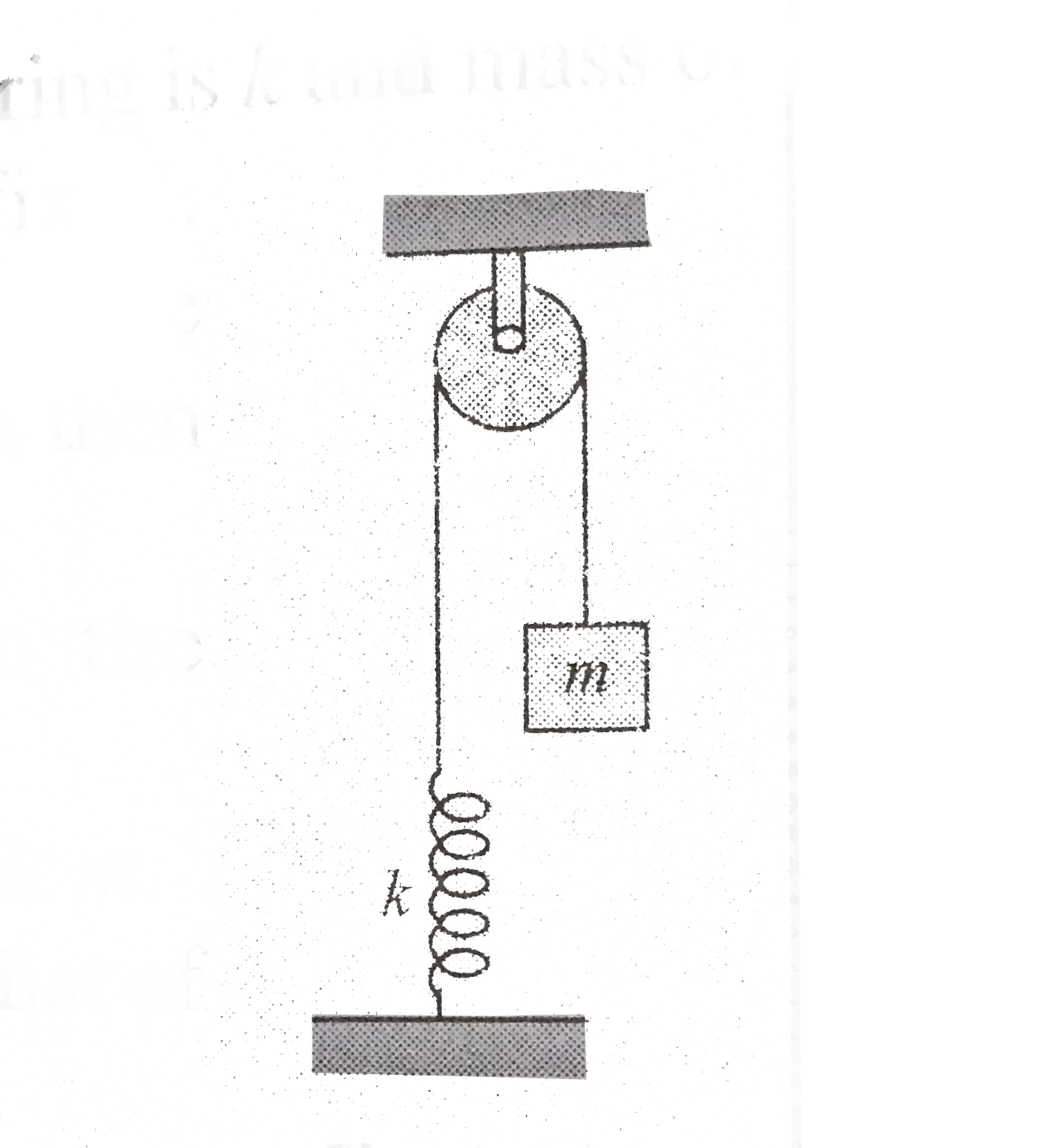 View Solution
View SolutionThe system shown in the following figure is in equilibrium and at rest. The spring and string are massless. Now, the string is cut. The acceleration of mass 2m and m, just after the string is cut, will be
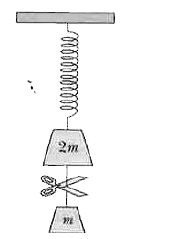 View Solution
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
 View Solution
View Solution

