With what minimum speed v must a small ball should be pushed inside a smooth vertical tube from a heoght h so that it may reach the top of the tube? Radius of the tube is R . 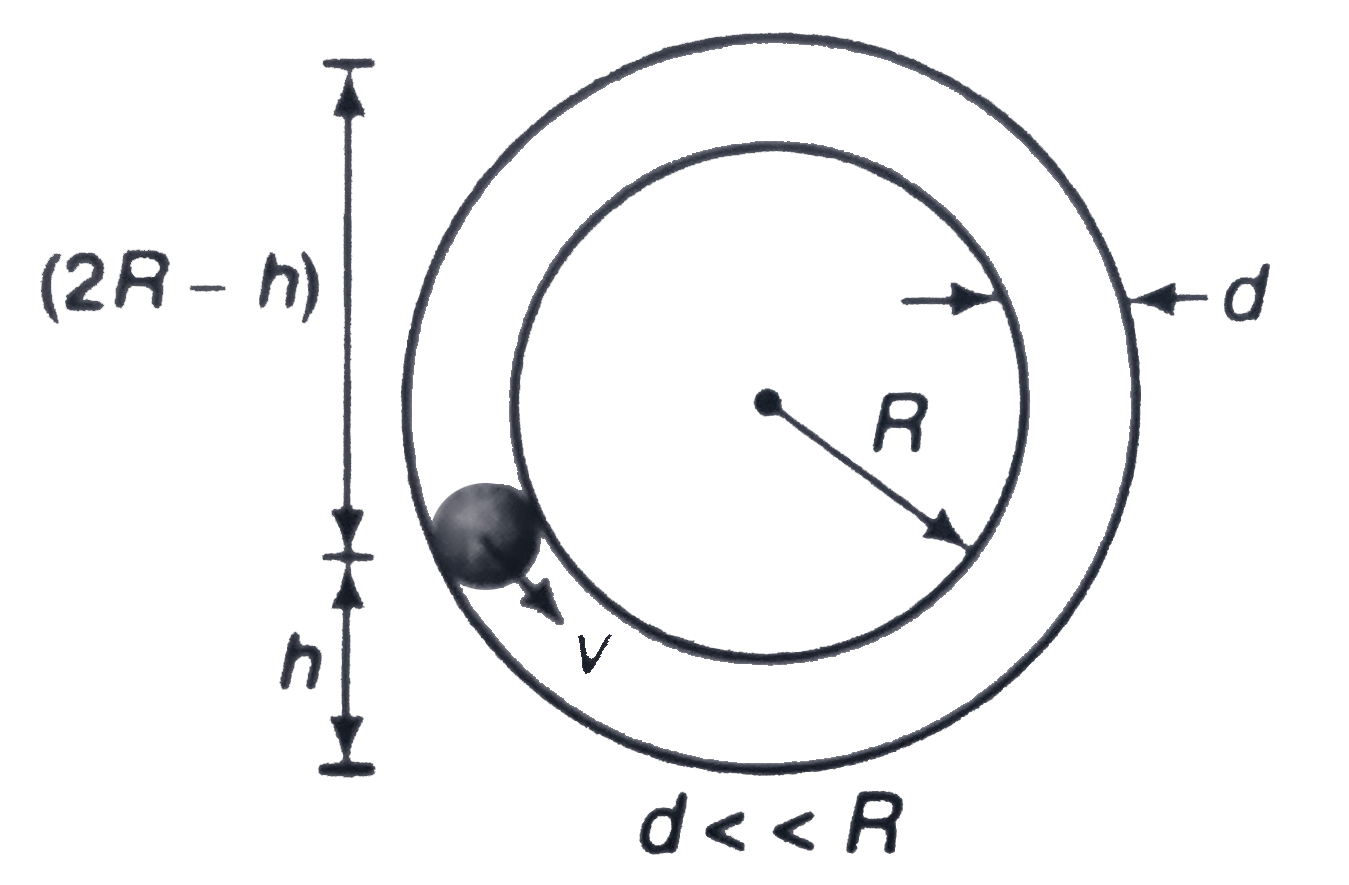
The correct Answer is:B
vtop=√v2−2g(2R−h)
To just complete the verticle circle vtop may be zero.
∴0=√v2−2g(2R−h)
or v=√2g(2R−h)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples2videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples5videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A ball is released from top of the smooth vertical, when i just leaves the contract form inner surface of the tube
_PHY_223_Q01.png) View Solution
View SolutionA smooth circular tube is held in a vertical position. A small ball which is free to slide inside the tube is held stationary at the highest position in the tube. If the ball is slightly displaced from its position of rest, show that the force exerted by the ball on the wall of the tube is given as mg(3cosθ−2) , where m is the mass of the ball and θ is the angular displacement from highest position. Upto what value of θ , this result will remain valid.
View Solution
Knowledge Check
- Question 1 - Select One
A small ball is pushed from a height h along a smooth hemispherical bowl of rodius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
A√2ghB√2g(R+h)C√2g(R−h)DNone of these - Question 2 - Select One
In a vertical smooth hollow thin tube, a block of same mass as that of tube is released as shown. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, the displacement of the tube will be (where ‘R’ is the mean radius of tube, assume that the tube remains in vertical plane).
 A2RπB4RπCR2DR
A2RπB4RπCR2DR - Question 3 - Select One
A capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
A23mBmC32mD94m
A large mass M and a small mass m hang at the two ends of string passing through a smooth tube. The mass m moves around in a circular path in a horizontal plane. The length of the string from the mass m to the top of the tube of the tube is l and θ is the angle this length makes with the vertical. What should be the frequency of rotation of the mass m so that M remains stationary ?
View SolutionA capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
View SolutionA ball of mass m is released from rest from a height H along a smooth, light and fixed tube having a semicircular portion so that the ball just reaches the top of the semicircle.
a. Find the radius of the semi-circle.
b. Find the maximum force imparted by the ball on the ground.
 View Solution
View SolutionWhen a capillary tube is dipped in a liquid, the liquid rises to a height h in the tube. The free liquid surface inside, the tube is hemispherical in shape. The tube is now pushed down so that the height of the tube outside the liquid is less than h. Then
View SolutionTwo capillary tubes of same radius r but of lengths l1 and l2 are fitted in parallel to the bottom of a vessel. The pressure to the bottom of a vessel. The pressure head is P. What should be the length of a singl tube of same radius that can replace the two tubes so that the rate of flow is same as before?
View Solution

