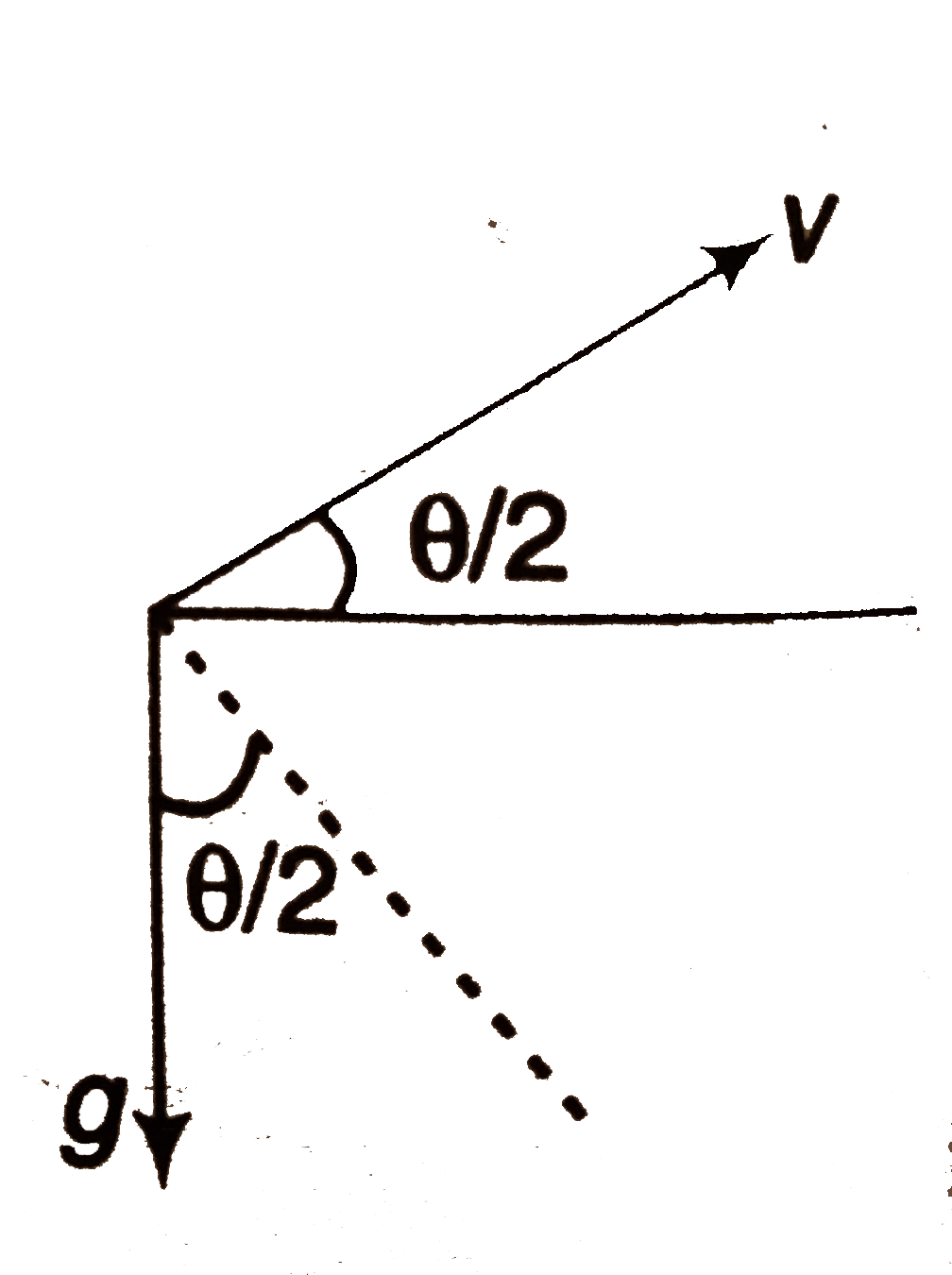
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes and angle θ2 with the horizontal?
Let v br the velocity at the desired point. Horizontal component of velocity remains unchaged. Hence,
vcos.θ2=ucosθ
v=ucosθcos.θ2
Radius accleration is the component of acceleration prependicular to velocity or
an=gcos(θ2)
v2R=cos(θ2)
Substituting the value of v from Eq. (i) in EQ. (II), we have radius of curvature
R=[ucosθcos(θ2)]2gcos(θ2)=u2cos2θgcos3(θ2)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.17videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.27videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples2videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A particle is projected with a speed u at an angle 60∘ with the horizontal.What is the radius of curvature of the parabola traced out by the projectile at a point where the particle velocity makes an angle 30∘ with the horizontal?
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle is fired from a point on the ground with speed u making an angle θ with the horizontal.Then
Athe radius of curvature of the projectile at the highest point is u2cos2θgBthe radius of curvature of the projectile at the highest point is u2sin2θgCat the point of projection magnitude of tangential acceleration is gsinθDat the point of projection magnitude of tangential acceleration is gcosθ - Question 2 - Select One
A particle is executing vertical SHM about the highest point of a projectile. When the particle is at the mean position, the projectile is fired from the ground with velocity u at an angle θ with the horizontal.The projectile hits the oscillating particle .Then, the possible time period of the particle is
AusinθgB2usinθgC2usinθ3gDall the above - Question 3 - Select One
A particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point C isAu2cos3θg2B2u2cos2θgCu2cos2θgDu2cos3θg
For a projectile first with velocity u at an angle θ with the horizontal.
 View Solution
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile.Projected with a speed u=√30 at angle θ=60∘ with the horizontal at a point where the particle velocity makes an angle θ/2 with the horizontal ?
View SolutionA projectile is fired with a velocity 'u' making an angle θ with the horizontal. Show that its trajectory is a parabola.
View SolutionA particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point B isView SolutionA particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point A isView Solution

