A ball falls vertically on an inclined plane of inclination α with speed v0 and makes a perfectly elastic collision. What is angle of velocity vector with horizontal after collision.
The correct Answer is:A, B
To solve the problem of finding the angle of the velocity vector with the horizontal after a ball falls vertically onto an inclined plane and makes a perfectly elastic collision, we can follow these steps:
Step 1: Understand the initial conditions
The ball is falling vertically with an initial speed v0 and strikes an inclined plane at an angle α with the horizontal.
Step 2: Analyze the collision
Since the collision is perfectly elastic, we can apply the principles of conservation of momentum and energy. However, for the purpose of finding the angle of the velocity vector after the collision, we can use the geometric properties of the collision.
Step 3: Determine the angles involved
- The angle of the inclined plane with the horizontal is α.
- The angle of incidence (the angle at which the ball strikes the plane) is 90∘ because the ball is falling vertically.
- The angle of reflection will be equal to the angle of incidence relative to the normal of the inclined plane.
Step 4: Calculate the angle of reflection
The normal to the inclined plane makes an angle 90∘−α with the horizontal. Therefore, the angle of incidence with respect to the normal is 90∘.
Using the law of reflection:
- The angle of reflection is equal to the angle of incidence. Thus, the angle of reflection with respect to the normal is also 90∘.
Step 5: Determine the angle of the velocity vector after collision
After the collision, the velocity vector of the ball will make an angle θ with the horizontal. Since the angle of reflection is 90∘ with respect to the normal, we can find the angle θ with the horizontal as follows:
θ=(90∘−α)+α=90∘
However, since the ball is reflecting off the inclined plane, the correct interpretation is that the angle of the velocity vector with the horizontal after the collision is:
θ=90∘−α
Final Answer
The angle of the velocity vector with the horizontal after the collision is 90∘−α.
---
The ball is falling vertically with an initial speed v0 and strikes an inclined plane at an angle α with the horizontal.
Since the collision is perfectly elastic, we can apply the principles of conservation of momentum and energy. However, for the purpose of finding the angle of the velocity vector after the collision, we can use the geometric properties of the collision.
- The angle of the inclined plane with the horizontal is α.
- The angle of incidence (the angle at which the ball strikes the plane) is 90∘ because the ball is falling vertically.
- The angle of reflection will be equal to the angle of incidence relative to the normal of the inclined plane.
The normal to the inclined plane makes an angle 90∘−α with the horizontal. Therefore, the angle of incidence with respect to the normal is 90∘.
- The angle of reflection is equal to the angle of incidence. Thus, the angle of reflection with respect to the normal is also 90∘.
After the collision, the velocity vector of the ball will make an angle θ with the horizontal. Since the angle of reflection is 90∘ with respect to the normal, we can find the angle θ with the horizontal as follows:
The angle of the velocity vector with the horizontal after the collision is 90∘−α.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion and Reason15videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective42videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.54videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A ball collides with an inclined plane of inclination θ after falling through a distance h. if it moves horizontal just after the impact, the coefficient of restitution is
Atan2θBcot2θCtanθDcotθ - Question 2 - Select One
In , if the collision were perfectly elastic, what would be the speed of deuteron after the collision ?
A2×106ms−1B4×106ms−1C6×106ms−1D8×106ms−1 - Question 3 - Select One
A ball is projected perpendicularly from an inclined plane of angle θ, with speed 'u' as shown. The time after which the projectile is making angle 45∘ with the inclined plane is :
AugsinθBugcosθCug{sinθ+cosθ}Dug{sinθ−cosθ}
A ball falls from height h over an inclined plane of inclination 30∘ as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_224_Q01.png)
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is component of the velocity of the block is √2gh , then θ is
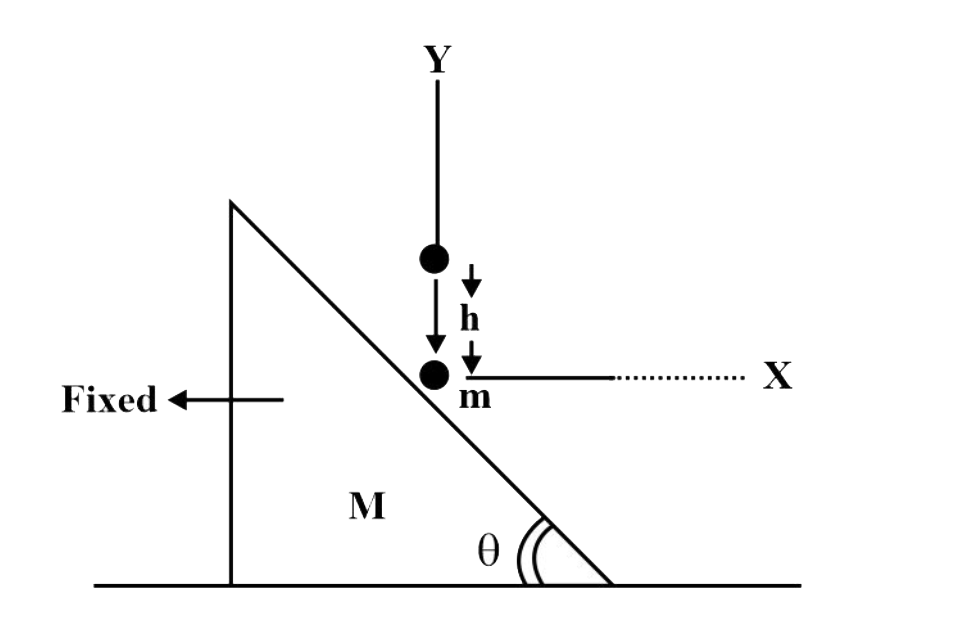
View SolutionA ball after falling a distance collides an inclined plane of inclination θ. If after the collision , the ball moves horizontally , find the coefficient of restitution.
View SolutionShow that in a perfectly elastic collision , the relative velocity of seperation after collision is equal to relative velocity of approach before collision .
View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.
View Solution