A uniform disc of mass 20 kg and radius 0.5 m can turn about a smooth axis through its centre and perpendicular to the disc. A constant torque is applied to the disc for 3s from rest and the angular velocity at the ned of that time is 240πrev/min find the magnitude of the torque. if the torque is then removed and the disc is brought to rest in t seconds by a constant force of 10 N applied tangentially at a point on the rim of the disc, find t
The correct Answer is:4
Angular impulse = change in angular momentum
∴τt=Iω=12mR2ω …(i)
∴τ=mR2ω2r
=(20)(0.5)2(2π×240π×60)2×3
=203N−m
During retardation using Eq. (i)
t=mR2ω2τ=mR2ω2(FR)
=mRω2F
=(20)(0.5)(2π×240π×60)2×10
=4s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions

A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionThe M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is MR22 . If one quarter of the disc is removed, the new moment of inertia of the disc will be
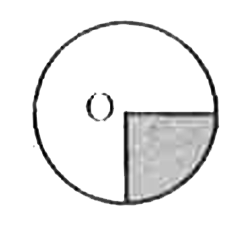
View Solution
Knowledge Check
A disc of mass 4 kg and radius 0.2 m, makes 20 rev/s, about an axis passing through its centre and perpendicular to the plane of the disc. The angular momentum of the disc is approximately equal to
A10 kg-m2/secB5 kg-m2/secC15 kg-m2/secD20 kg-m2/secA disc of mass 2 kg and diameter 40 cm is free to rotate about an axis passing through its centre and perpendicular to its plane. If a force of 50 N is applied to the disc tangentially Its angular acceleration will be
A100rad/s2B25rad/s2C250rad/s2D500rad/s2Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
AMR22−M(4R3π)2BMR22−M(√24R3π)2CMR22+M(4R3π)2DMR22+M(√24R3π)2
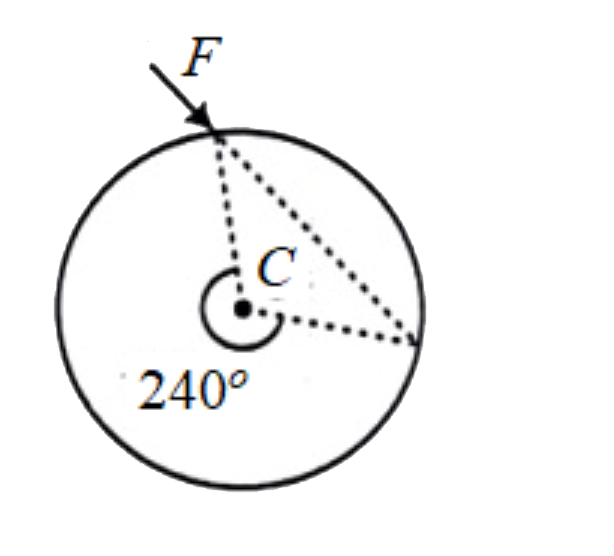
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
View SolutionA homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis with an angular velocity of 4 rad/s. the linear momentum of the disc is
View SolutionA disc of radius 10 cm can rotate about an axis passing through its centre and perpendicular to its plane. A force of 10 N is applied along the tangent in the plane of the disc. If the moment of inertia of the disc about its centre is 5kgm2, then the increase in the angular velocity of the disc in 10 s will be
View Solution
