A planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
Using conservation of angular momentum
mυprp=mυara
As velocitties are perpendicular to the radius vectors at apogee and perigee.
⇒υprp=υara
Using conservation of energy,
−GMmrp+12mυ2p=−GMmra+12mυ2a
BY solving, the above equations,
υp=√2GMrarp(rp+ra)
L=mυprp=m√2GMrpra(rp+ra)
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Exercise 13.1
Explore 5 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Exercise 13.2
Explore 9 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Solved Examples
Explore 16 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
A planet of mass m moves along an ellipse around the Sun so that its maximum and minimum distances from the Sun are equal to r1 and r2 respectively. Find the angular momentum M of this planet relative to the centre of the Sun.
View SolutionA planet of mass m moves along an ellipse around the sum of mass M so that its maximum and minimum distances from sum are a and b respectively. Prove that the angular momentum L of this planet relative to the centre of the sun is L=m√2GGMab(a+b)
View Solution
Knowledge Check
A planet of mass m moves along an ellipse around the sun so that its maximum and minimum distance from the sun are equal to r1 and r2 respectively. Find the angular momentum of this planet relative to the centre of the sun. mass of the sun is M.
Am√2GMr1r2(r1+r2)2Bm ⎷2GMr21r22(r1+r2)2Cm ⎷2GMr21r22(r1+r2)Dm√2GMr1r2(r1+r2)A comet of mass m moves in a highly elliptical orbit around the sun of mass M the maximum and minium distacne of the comet from the centre of the sun are r1 and r2 respectively the magnitude of angular momentum of the comet with respect to the centre of sun is
A[GM1r1+r2]1/2B[GMmr1r1+r2]1/2C[rGM2r1r2r1+r2]1/2D[2GMm2r1r2r1+r2]1/2A planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
Ar3/21Br3/22C(r1−r2)3/2D(r1+r2)3/2
A planet of mass moves alng an ellipes around the sun so that its maximum distance from the sum are equal to r1 and r2 respectively . Find the angular momenture L of this planet relative to the centre of the sun.
[Hint :L Rember that at the maximum and minimum distance velocity is perpendicular to tthe position vectors of the planet . Apply the princples of conservation of angula r momenture and energy .]
View SolutionA planet of mass m moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2, respectively. Find the relation between the time period of the planet in terms of r1 and r2.
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
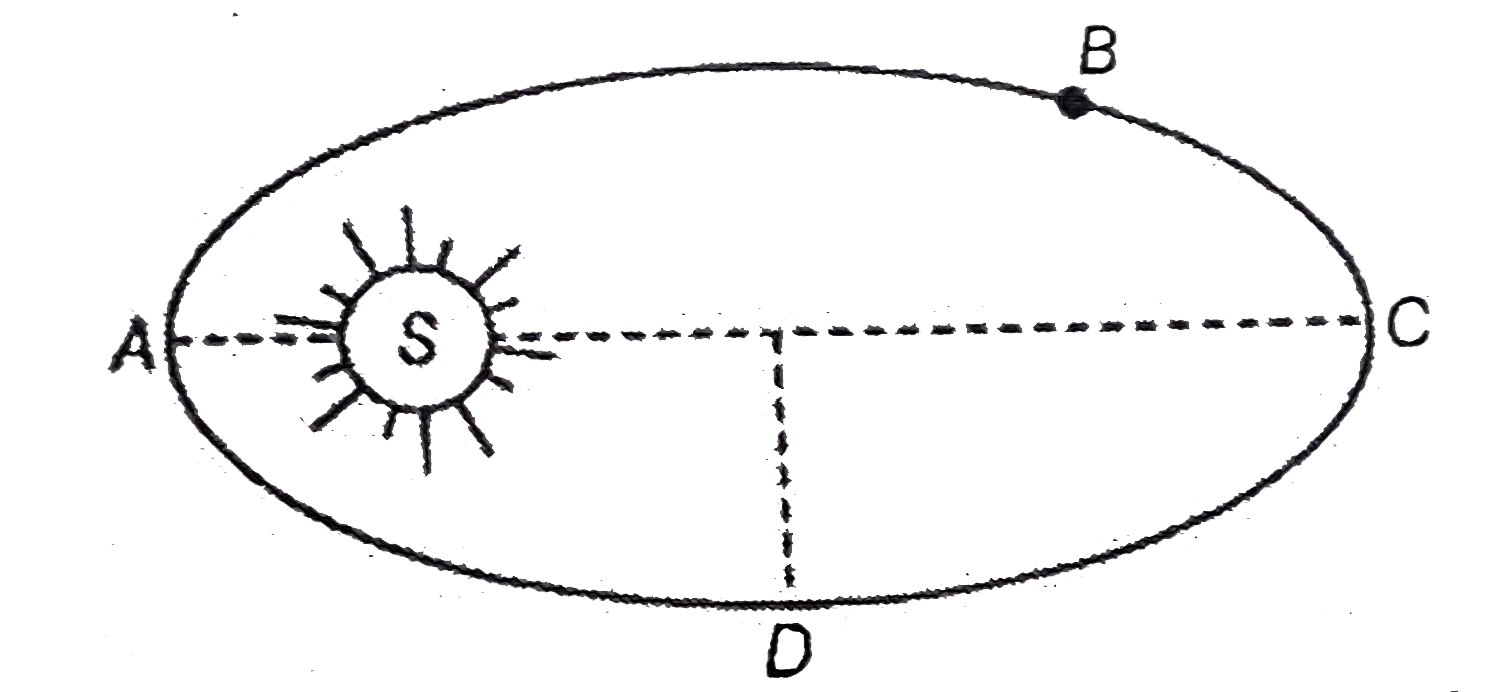
View SolutionA planet of small mass m moves around the sun of mass M along an elliptrical orbit such that its minimum and maximum distance from sun are r and R respectively. Its period of revolution will be:
View Solution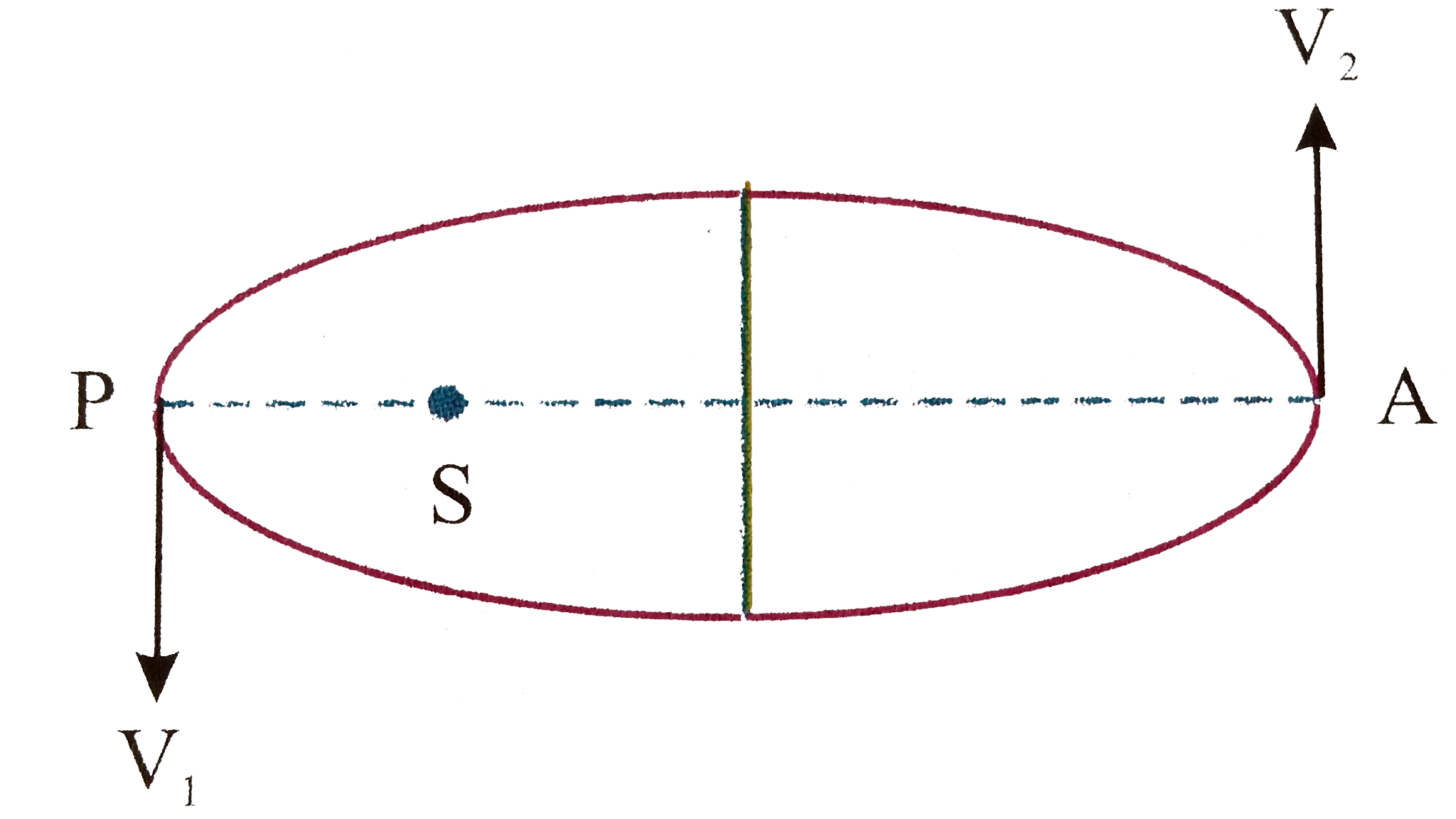
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
View Solution