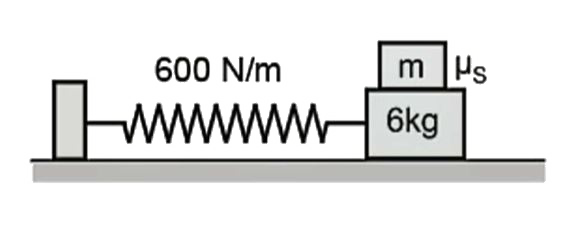
With the assumption of no slipping, determine the mass m of the block which must be placed on the top of a 6kg cart in order that the system period is 0.75s. What is the minimum coefficient of static friction μs for which the block will not slip relative to the cart is displaced 50mm from the equilibrium position and released? Take (g=9.8m/s2).

The correct Answer is:A, B, C
(a) T=2π√m+6600 (T=2π√mK)
or 0.75=2π√m+6600
∴m=(0.75)2×600(2π)2−6
=2.55kg
(b) Maximum acceleration of SHM is,
amax=ω2A (A = amplitude)
i.e. maximum force on mass 'm' is mω2A which is bieng provided by the force of friction between the mass and the cart. Therefore,
μsmg≥mω2Aorμs≥ω2Ag or μs≥(2πT)2.Ag
or μs≥(2π0.75)2(0.059.8)
(A=50mm)
or μs≥0.358
Thus, the minimum value of mu_(s) should be 0.358.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 6
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 7
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 4
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
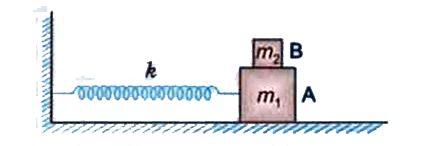
View SolutionA block of mass m is placed on the top of a 6kg cart such that the time period of the system is 0.75 s assuming there is no slipping. If the cart is displaced by 50 mm from its equilibrium position and released, then the coefficient of static friction μs between block and cart is just sufficient to prevent the block from sliding. The value of m and μs respectively are (Take g=9.8m/s2)
View Solution
Knowledge Check
Two blocks lie on each other and connected to a spring as shown in figure. What should be the mass of blocks A placed on block B of mass 6 kg, so that the system's period is 0.75 s ? Assume no slipping, what should be the minimum value of coefficient of static friction μs for which block A will not slip relative to block B, if block B is displaced 50 mm from equilibrium position and released ?
 A2 kg, μs = 0.4B4.2 kg, μs = 0.358C2.56 kg, μs≥ 0.358D2.56 kg, μs≤ 0.358
A2 kg, μs = 0.4B4.2 kg, μs = 0.358C2.56 kg, μs≥ 0.358D2.56 kg, μs≤ 0.358A marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
A(a) 0.02B(b) 0.03C(c) 0.04D(d) 0.06A marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
A0.02B0.03C0.06D0.01
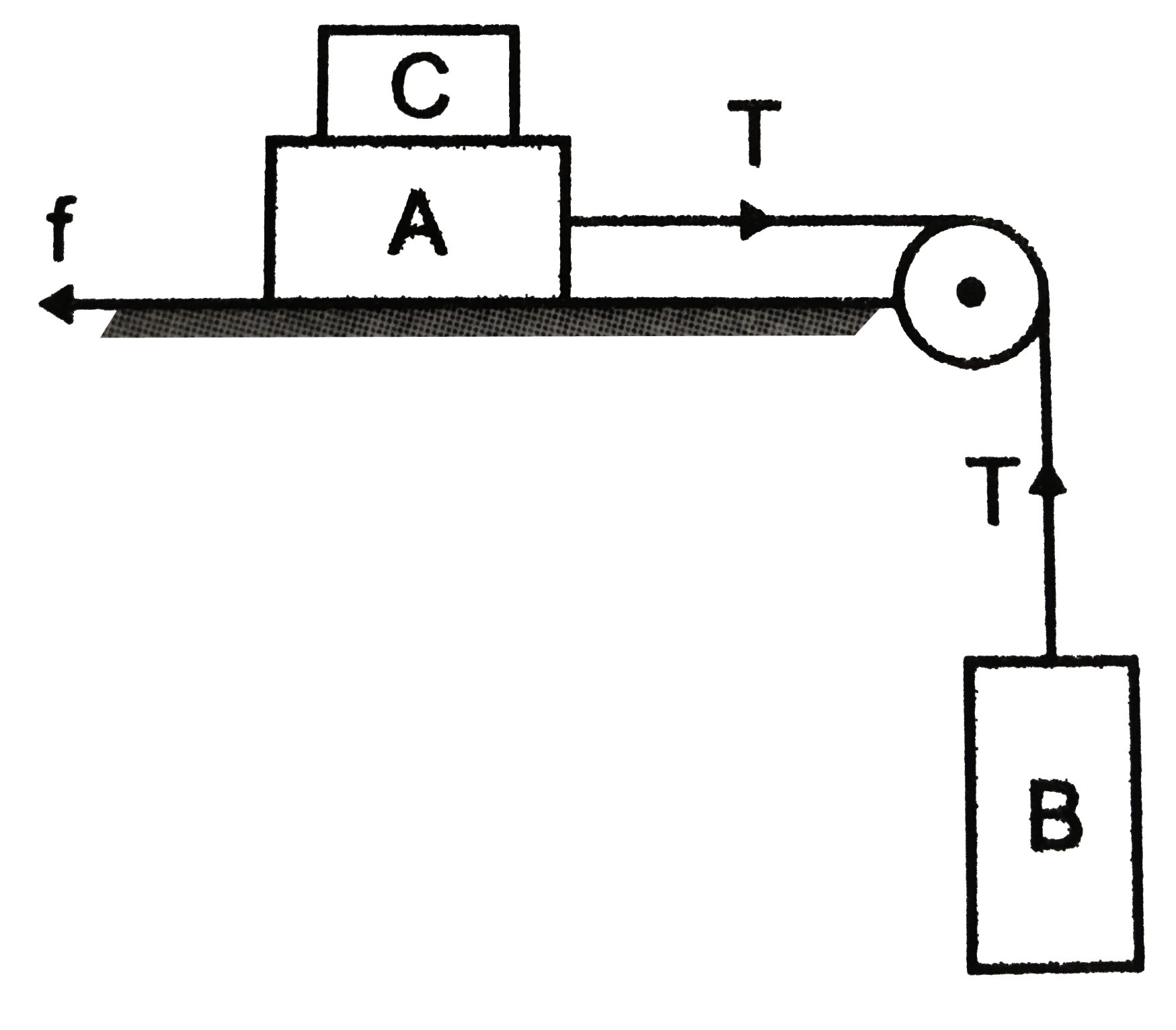
In the masses of A and B are 10 kg and 5 kg . Calculate the minimum mass of C which may stop A from slipping Coefficient of static friction between block A and table is 0.2
 .
.
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of mass 2 kg is placed on the floor . The coefficient of static friction is 0.4 . If a force of 2.8 N is applied on the block parallel to floor , the force of friction between the block and floor is : (Taking g = 10m/s2)
View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)

View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View Solution
