Assertion : Aparticle is under SHM along the x - axis. Its mean position is x=2, amplitude is A=2 and angular frequency ω. At t=0, particle is at origin, then x - co-ordinate versus time equation of the particle will be x=−2cosωt+2.
Reason : At t=0 , particle is at rest.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:B
y=(−Acosωt) at the particle starts from −A
So, displacement from the mean position will be −Acosωt.
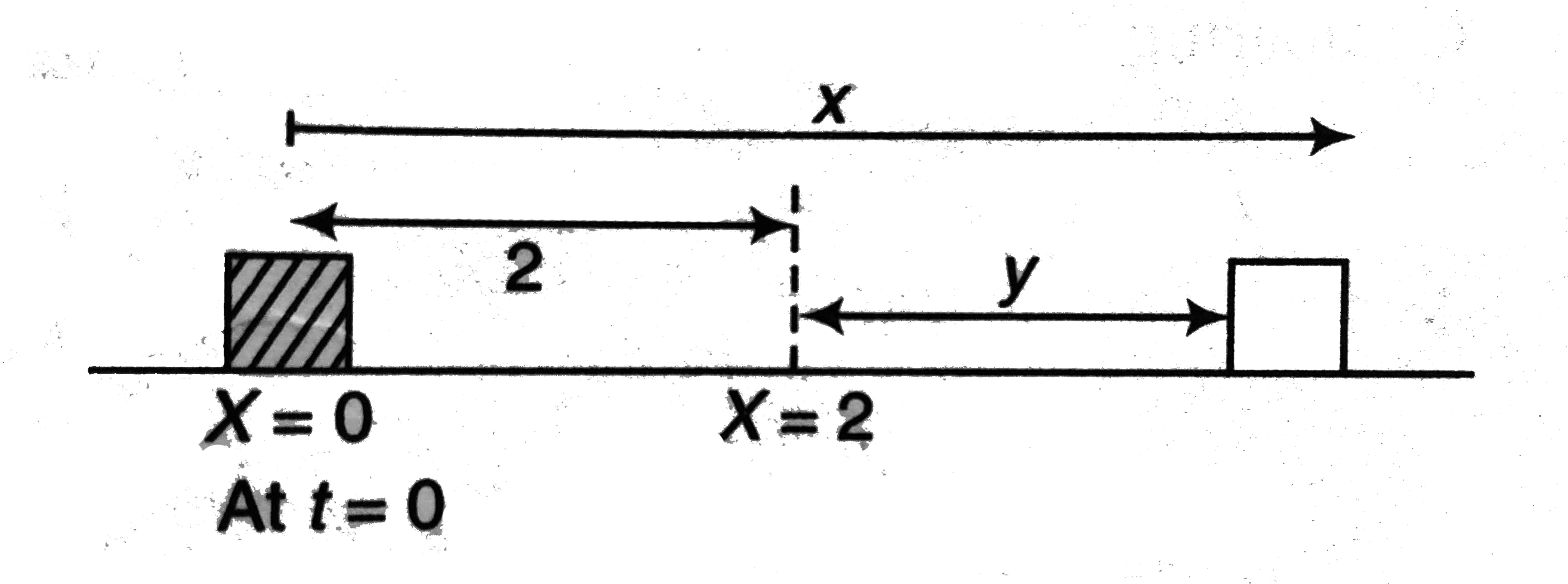
∴x=y+2
=−2cosωt+2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct24videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective39videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Miscellaneous Examples8videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
Similar Questions
Knowledge Check
- Question 1 - Select One
Equation motion of a particle is given as x=Acos(ωt)2. Motion of the particle is
APeriodic and oscillatoryBPeriodic but not oscillatoryCOscillatory but not periodicDNeither oscillatory nor periodoic - Question 2 - Select One
The motion of a particle is given by x=Asinωt+Bcosωt. The motion of the particle is
Anot simple harmonicBsimple harmonic with amplitude A + BCsimple harmonic with amplitude (A+B)2Dsimple harmonic with amplitude √A2+B2 - Question 3 - Select One
A particle starts from rest at the extreme position and makes SHM with an amplitude A and angular frequency ω. Its displacement at time 't' is
AAsinωtBAcosωtCAsin2πωtDAcos2πωt
A particle moves along the x-axis according to the equation x=asinωt+bcosωt. The motion is simple harmonic with
View SolutionA particle executes SHM along x-axis with an amplitude A, time period T with origin as the mean position. At t = 0, if the particle starts in the +ve x-direction from the origin the minimum time in which it will be at x=−A/2 will be
View SolutionTwo particles are in SHM with same amplitude A and same regualr frequency ω. At time t=0, one is at x =+A2 and the other is at x=−A2. Both are moving in the same direction.
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is
 View Solution
View Solution

