An object suspended from a spring exhibits oscillations of period T. Now ,the spring is cut in half and the two halves are used to support the same object, as shown in figure. Show that the new period of oscillation is T/2.
 .
.
The correct Answer is:A
k∝1l
Length is halved ,so value of force constant of each part will become 2k. Now net force constant of 2k and 2k as shown in figure will becomes 4k.
T=2π√mk
or T∝1√k
k has becomes 4 times. Therefore, T will remain half.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View Solution
Knowledge Check
An object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
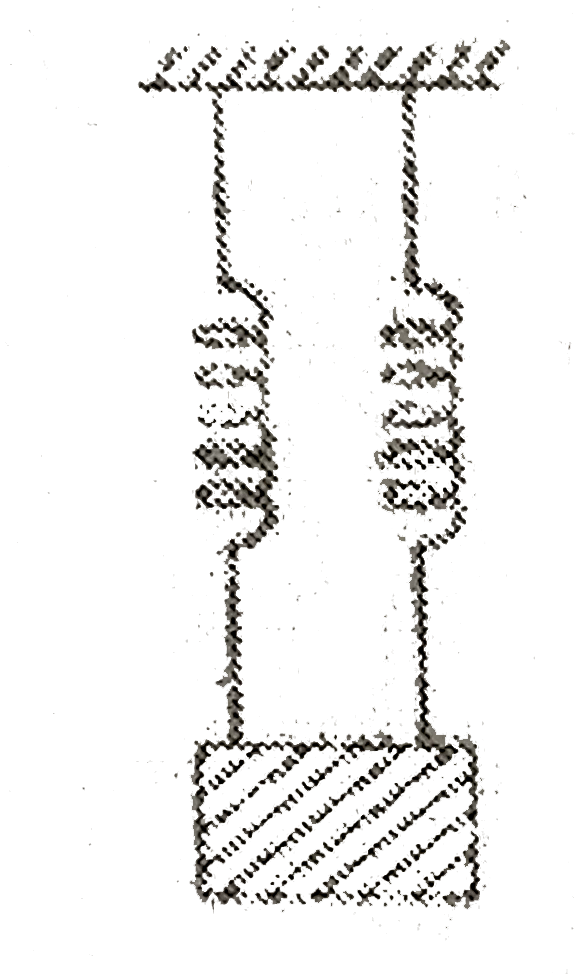 AT√2B2TCT2DT2√2
AT√2B2TCT2DT2√2An object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspsended with two halves as shown in figure. The new time period of oscillation will become
 AT√2B2TCT2DT2√2
AT√2B2TCT2DT2√2A spring has a certain mass suspended from it and its period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is now
AT2BT√2C√2TD2T
A simple harmonic motion oscillator has two springs of spring constant k and other two of spring constant 2k, arranged as shown in the figure. Calculate the time period of oscillator.
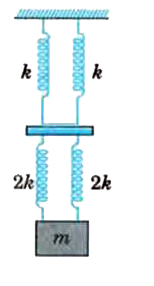
View SolutionA bar magnet suspended freely has period of oscillation of 2s. Now, the bar magnet is broken into equal halves and one-half is suspended to oscillate freely in the same magnetic field. Find the time period of oscillation of this half of the magnet.
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now T2. The ratio of T2/T1 is
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA spring of spring constant K is cut equal parts of which t part are places in particle and connected will mass m shown in figure The time period of oscilation motion of mass m is
View Solution
