A steel ball of mass m falls in a viscous liquid with terminal velocity v, then the steel ball of mass will fall in the same liquid with terminal velocity
The correct Answer is:B
To solve the problem, we need to understand the relationship between the mass of the steel ball, its radius, and the terminal velocity when it falls through a viscous liquid.
1. Understanding Terminal Velocity:
The terminal velocity vt of an object falling through a viscous fluid is given by the balance of forces acting on it. The gravitational force is balanced by the drag force due to the viscosity of the liquid.
2. Relation Between Mass and Radius:
The mass m of the steel ball is related to its volume V and density ρ as follows:
m=ρV
For a sphere, the volume V is given by:
V=43πr3
Therefore, we can express mass in terms of radius:
m=ρ(43πr3)
This shows that mass is directly proportional to the cube of the radius:
m∝r3
3. Finding the New Radius:
If the mass of the new steel ball is 8m, we can set up the equation:
8m=ρ(43πr′3)
Since m∝r3, we can write:
8m∝r′3
Thus, if m∝r3, then:
r′3=8r3⟹r′=2r
4. Finding the Terminal Velocity:
The terminal velocity vt is proportional to the square of the radius:
vt∝r2
For the new radius r′=2r:
v′∝(r′)2=(2r)2=4r2
Therefore, if the original terminal velocity is v, the new terminal velocity v′ will be:
v′=4v
Final Answer:
The terminal velocity of the steel ball of mass 8m falling in the same viscous liquid will be 4v.
The terminal velocity vt of an object falling through a viscous fluid is given by the balance of forces acting on it. The gravitational force is balanced by the drag force due to the viscosity of the liquid.
The mass m of the steel ball is related to its volume V and density ρ as follows:
m=ρV
For a sphere, the volume V is given by:
V=43πr3
Therefore, we can express mass in terms of radius:
m=ρ(43πr3)
This shows that mass is directly proportional to the cube of the radius:
m∝r3
If the mass of the new steel ball is 8m, we can set up the equation:
8m=ρ(43πr′3)
Since m∝r3, we can write:
8m∝r′3
Thus, if m∝r3, then:
r′3=8r3⟹r′=2r
The terminal velocity vt is proportional to the square of the radius:
vt∝r2
For the new radius r′=2r:
v′∝(r′)2=(2r)2=4r2
Therefore, if the original terminal velocity is v, the new terminal velocity v′ will be:
v′=4v
The terminal velocity of the steel ball of mass 8m falling in the same viscous liquid will be 4v.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Level 1 Subjective
Explore 36 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Subjective Question
Explore 2 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Assertion and Reason
Explore 1 Video
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A lead sphere acquires a terminal velocity υ when falls in a vicous liquid. The terminal velocity attained by another lead sphere of radius three times in the same liquid will be _______
View SolutionA lead sphere acquires a terminal velocity v when falls in a viscous liquid. What will be the terminal velocity attained by another lead sphere of radius three times in the same liquid ?
View Solution
Knowledge Check
When a sphere falling in a viscous fluid attains a terminal velocity, then
Athe net force acting on the sphere is zeroBthe drag force balances the buoyant forceCthe drag force balances the weight of the sphereDthe buoyant force balances the weight and drag forceRain drops fall with terminal velocity due to
AbuoyancyBviscosityClow weightDsurface tensionA small lead ball is falling freely in a viscous liquid The velocity of the ball
Agoes on increasingBgoes on decreasingCremains constnatDfirst increases and then becomes constant
A metallic sphere of mass M falls through glycerine with a terminal velocity v. If we drop a ball of mass 8M of same metal into a column of glycerine, the terminal velocity of ball will be
View SolutionA sphere of mass M and radius R is falling in a viscous fluid. The terminal velocity attained by the falling object will be alphaortional to :
View SolutionA small sphere of volume V falling in a viscous fluid acquires a terminal velocity vt. The terminal velocity of a sphere of volume 8V of the same material and falling in the same fluid will be :
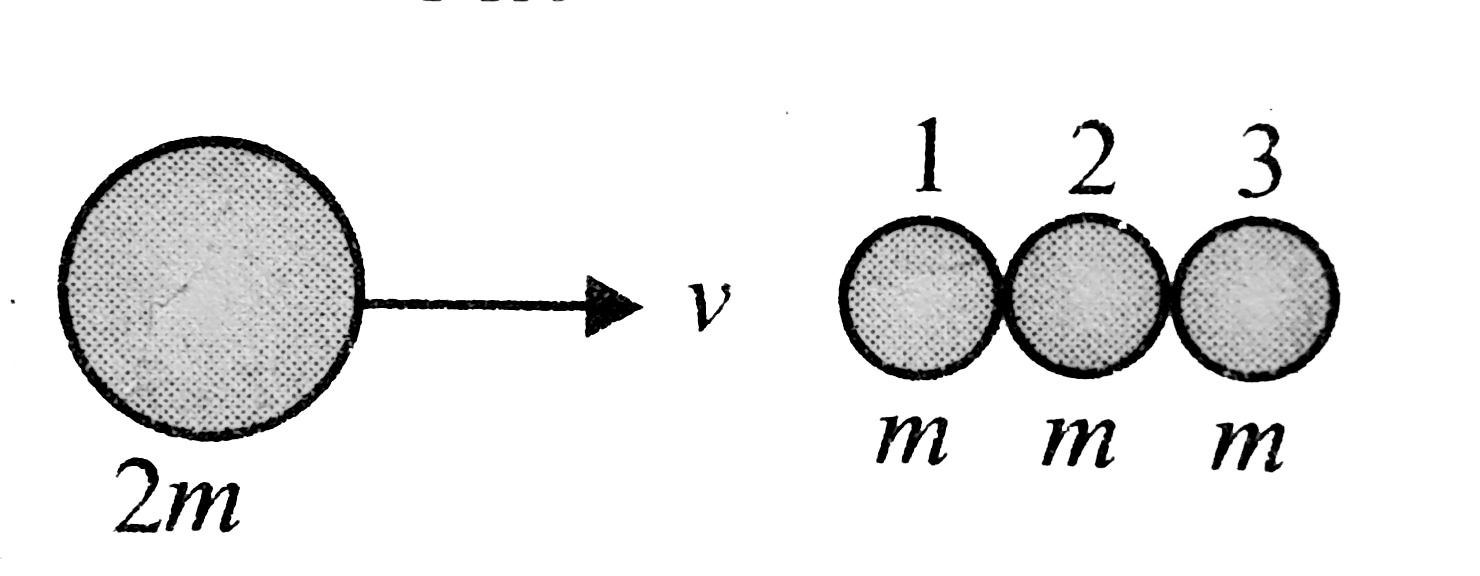
View SolutionA steel ball of mass 2m suffersone-dimensional elastic collision with a row of three steel balls, each of mass m. If mass 2m has collided with velocity v and the three balls numbered 1,2,3 were initially at 2. rest, then after the collision
View SolutionA small metal ball of mass m is dropped in a liquid contained in a vessel , attains a terminal velocity v . If a metal ball of same material but of mass 8 m is droped is same liquid then the terminal velocity will be
View Solution