Two boats of base areas A1 and A2, connected by a string are being pulled by an extermal force F0. The velosity is η and depth of the water body is H. when the system attains a constant speed. The tension in the trhead will be

F0(A1A2)
F0A2(A1+A2)
F0A1(A1+A2)
F0(A2A1)
The correct Answer is:C
Viscous force F∝(area)
So let F=kA
F0=k(A1+A2) …(i)
and T=kA1 ….(ii)
Divinding Eq, (ii) by Eq. (i) we get,
TF0=A1A1+A2
∴T=F0A1A1+A2.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two blocks of mass m1andm2 are connected by a spring of force constant k. Block of mass m1 os pulled by a constant force f2 [see fig 4E.19 (a)] find the maximum elongation in the spring .
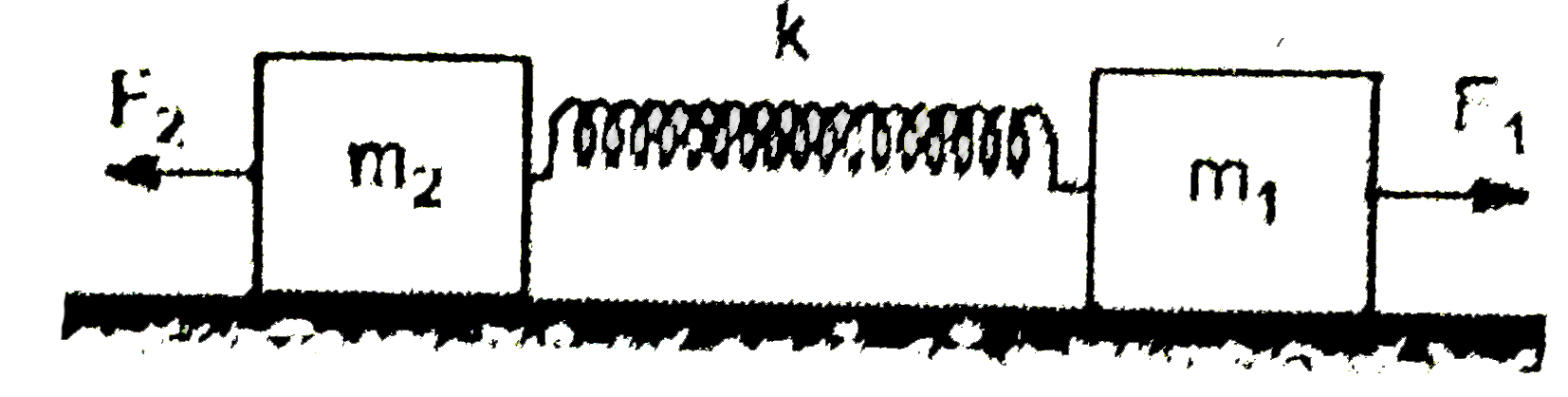
View SolutionTwo block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
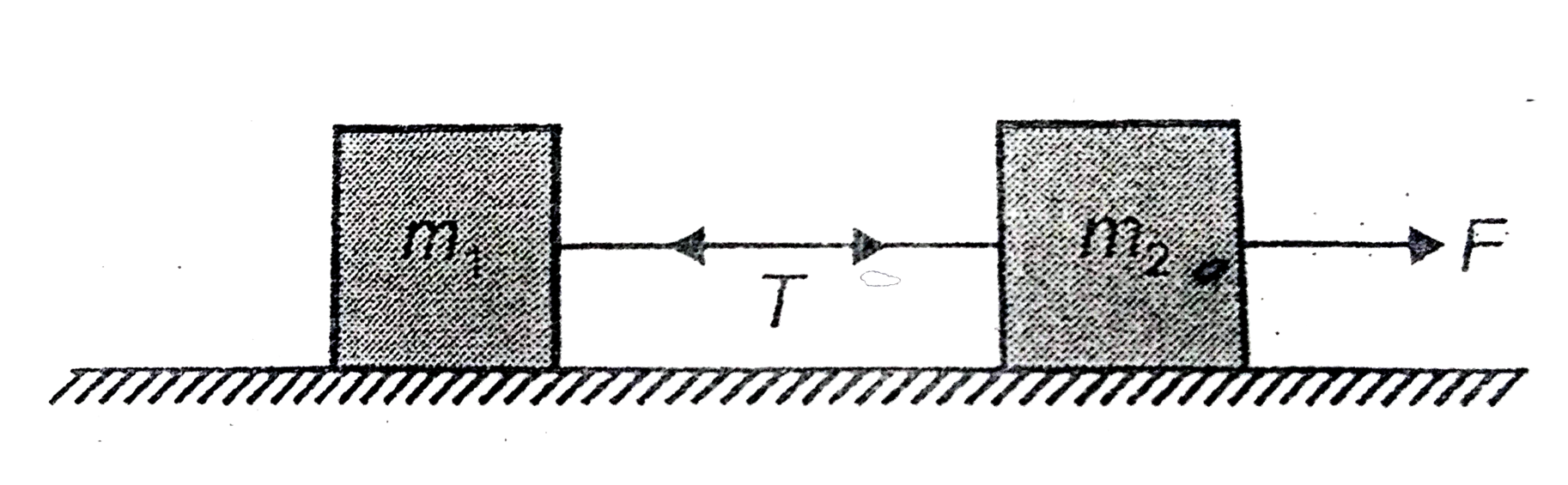
View Solution
Knowledge Check
Two blocks are connected by a string and pulled by a force F=50N. If the coefficient of friction between the blocks and the ground is 0.2, friction force between the block B and the ground is :
 A20NB30NC40NDzero
A20NB30NC40NDzeroConsider a system of masses M1 and M2(M1>M2) connected by a massless string in fig the system is pulled by a force F from the side of mass M1 and in fig
(b) the system is pulled by the same force F from the side of mass M2 then:
 Aacceleration in the two cases is same and tension in the string connecting M1andM2 is also sameBacceleration of system in (a) is more than in (b) while tension in the string is same in both casesCacceleration of system in both cases is same but tension in the string in (a) is more than in (b)Dacceleration of system in both cases is same but tension in the string in (a) is less than in (b)
Aacceleration in the two cases is same and tension in the string connecting M1andM2 is also sameBacceleration of system in (a) is more than in (b) while tension in the string is same in both casesCacceleration of system in both cases is same but tension in the string in (a) is more than in (b)Dacceleration of system in both cases is same but tension in the string in (a) is less than in (b)Consider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
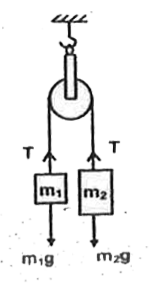
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?A75NB150NC300ND500N
Two blocks are attached by a light inextensible string and the system is pulled by applying a force F0 as shown in the diagram. Find the acceleration of each block and tension in the string.

View SolutionTwo blocks of masses m1=2kgandm2=5kg hang over a massless pulley as shown in the fig A force F0=100N acting at the axis of the pulley accelerates the system upwards Find
(a) the acceleration of each mass
(b) the tension in the string.

View SolutionThere are two tanks next to each other having cross sectional area A1 and A2. They are interconnected by a narrow pipe having area of cross section equal to A0. Initial height of water in the two tanks is h1 and h2 meaured from the level of the pipe. Assume that the flowis ideal and behaves in a way similar to the discharge in air. Calculate the time needed for the water level in two tanks to become same.
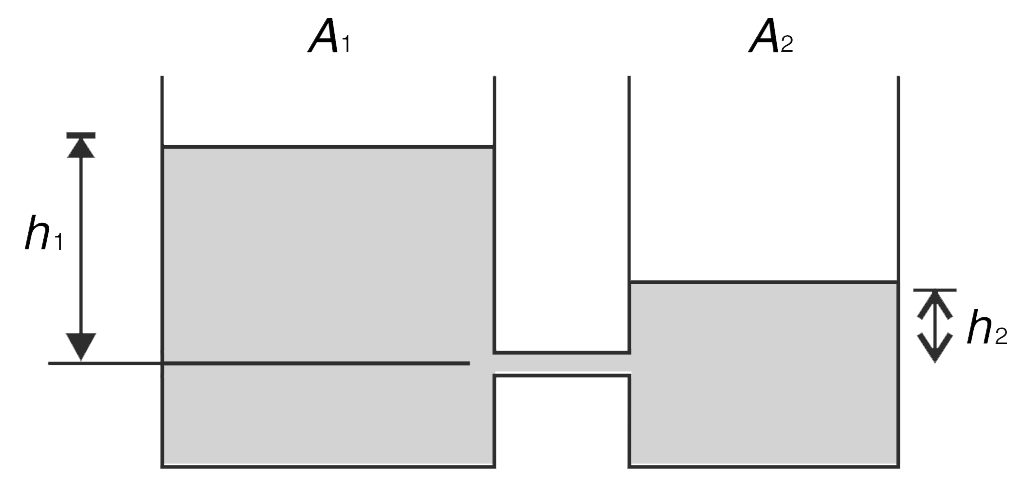
View SolutionTwo particles of masses m1 and m2 are connected with a rigid rod of length l. If a force F acts perpendicular to the rod then (a1&a2 are instantaneous of m1&m2)

View SolutionTwo blocks of mass 4kg and 2kg are connected by a heavy string and placed on rough horizontal plane. The 2 kg block is pulled with a constant force F. the coefficent of friction between the blocks and the ground is 0.5. what is the value of F so that tension in the string is constant throughout the length? (g=10m/s2)
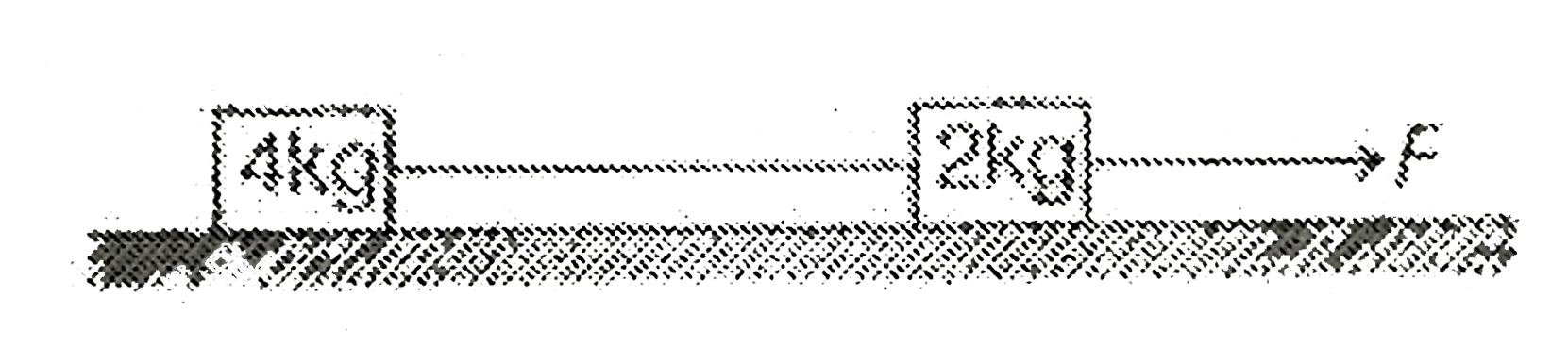
View Solution
