A rectangular tank of height 10m filled with water, is placed near the bottom of a plane inclined at an angle 30∘ with horizontal. At height h form bottom a small hole is made (as shown in figure) such that the stream coming out from hole, strikes the inclined plane normally.Calculate h.

The correct Answer is:C
v=√2g(10−h)
Component of its velocity parallel to the plane is vcos30∘
Let the stream strikes the plane after time t. Then
0=vcos30∘−gsin30∘t
∴t=vcos30∘g
Further x=vt=v2cot30∘g
√3y
or, v2cot30∘g=√3(h−12>2)
∴√3v2g=√3(h−g2v2cot230∘G2)
or, v2g=h−32v2g
∴52v2g=h or 5(10−h)=h
∴h=8.33m
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.11videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.21videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based7videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A heavy block of length b and height h is placed at rest on a rough inclined plane of inclination θ with the horizontal, as shown in figure.
 View Solution
View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A water tank of height H, completely filled with water is placed on a level ground. It has two holes one at a depth h from top and the other at height h form its base. The water ejecting from
Aboth the holes will fall at the same spotBupper hole will fall farther than that form the lower holeCupper hole will fall closer than that form the lower holeDmore information is required. - Question 2 - Select One
A hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2 - Question 3 - Select One
A ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
A12 mB60 mC120 mD600 m
A one kg rolling on a smooth horizontal surface at 20ms−1 comes to the bottom of an inclined plane making an angle of 30∘ with the horizontal. Calculate K.E. of the ball when it is at the bottom of incline. How far up the incline will the ball roll ? Neglect friction.
View SolutionOn the wall of a cylindrical water tank, two holes are made as shown in figure. Water coming out from these holes hits the ground at the same point. What will be the ration h1h2?
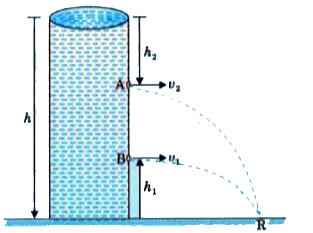 View Solution
View SolutionA large tank having a small hole at the bottom is filled with water to a height h. If the stream of water coming out of the hole is directed vertically upwards it will :
View SolutionA tank with base area L2 is filled with a liquid to height H. The tank is acceleration horizontally with acceleration a as shown in figure. If a small hole is made at the point A. then it is observed that the liquid does not come out of the tank. The magnitude of acceleration should be
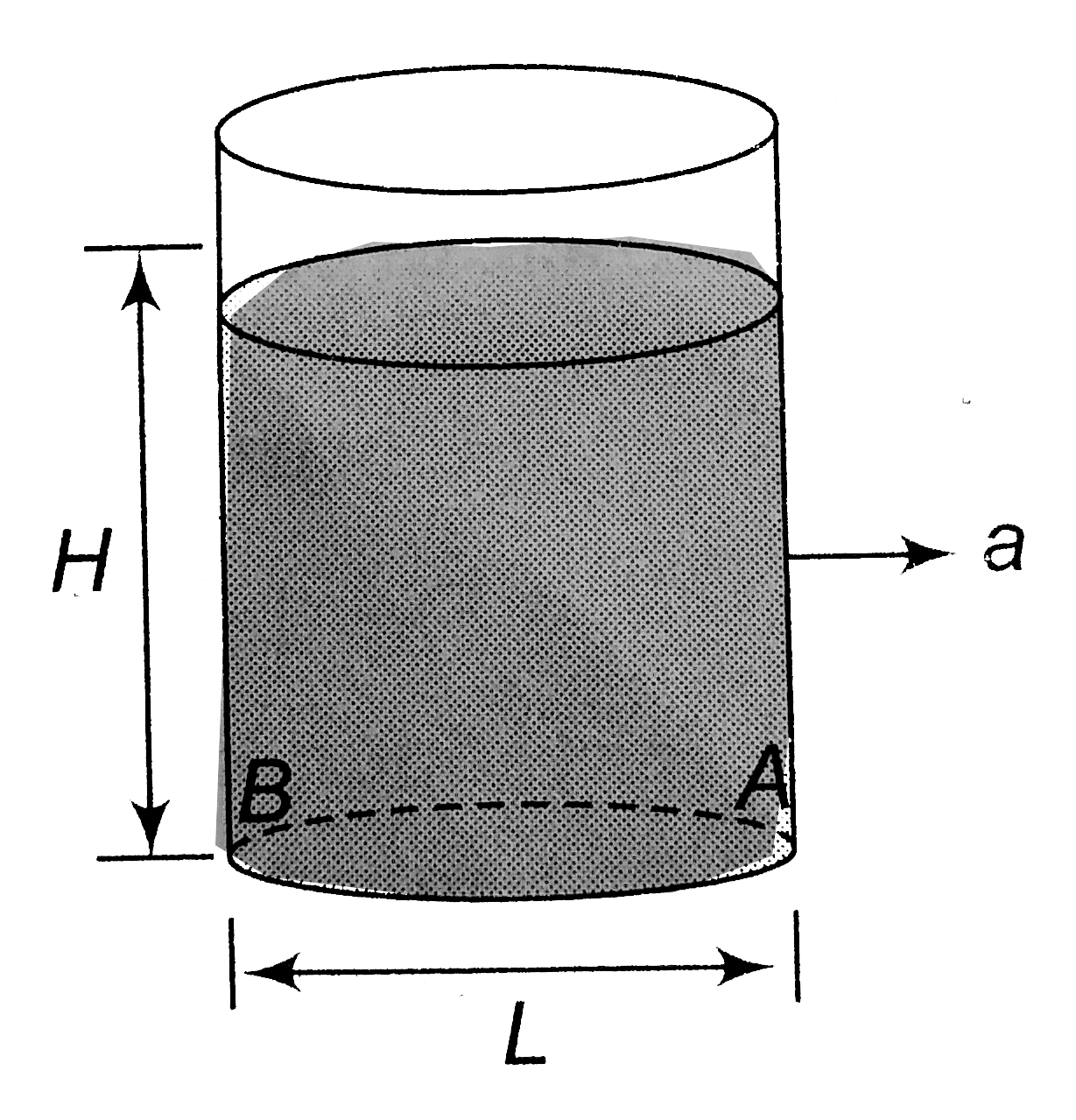 View Solution
View SolutionA tank of height H is fully filled with water. If the water rushing from a hole made in the tank below the free surface , strikes the floor at a maximum horizontal distance , then the depth of the hole from the free surface must be
View Solution

