A stretched wire is oscillating in third overtone mode. Equation of transverse stationary wave produced in this wire is
Here, x is in metres. Find the length of the wire.
The correct Answer is:B, C
From the given equation we can see that
= 1/3m
Now, third overtone mode means four loops as shown below
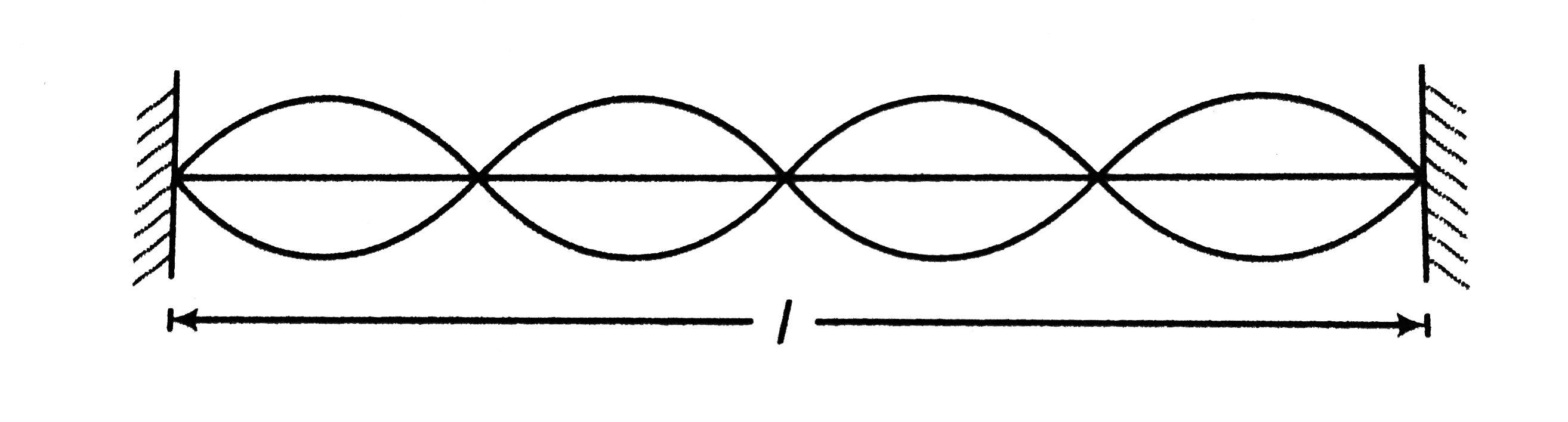
One loop size is , therefore total length of wire,
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Example Type 21videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Example Type 31videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective8videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
- BOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
Similar Questions
Following is given the eqution of a stationary wave (all in SI units)
y = (0.06)sin (2πx)cos(5πt)
Match of following.
View SolutionFind the wrong statement from the following about the equation of stationary wave given by Y=0.04cos(πx)sin(50πt) m where tis in second. Then for the stationary wave.
View Solution
Knowledge Check
- Question 1 - Select One
The equation of a stationary a stationary wave is represented by
y=4sin(π6)(cos20πt)
when x and y are in cm and t is in second.
Wavelength of the component waves isA4 cmB20 cmC12 cmD6 cm - Question 2 - Select One
A wave is represented by the equation y=7sin{π(2t−2x)} here x is in metres and t in seconds. The velocity of the wave is
A1m/sB2m/sC5m/sD10m/s - Question 3 - Select One
Find the incorrect from the following the equation of a stationary wave is given by y=6cos(πx5)sin(4πt), where y and x are in cm and t is in second. Then, for the stationary wave
Aamplitude=3cmBwavelength=5cmCfrequency=20HzDvelocity=2m/s
The equation of a stationary wave is given by
y=6sinπ/xcos40πt Where y and x are given in cm and time t in second. Then the amplitude of progressive wave isView SolutionThe equation of a plane progressive wave is given by
y=2cos(100πt−πx20)
where x and y are in cm and t is in second. The wavelength of the wave isView SolutionFine the wrong statement from the following :
The equation of a stationary wave is given by y=6cos(πx5)sin(40πx),where y and x are in cm and t is in second. Then for the stationary wave,View SolutionA steel wire having cross-sectional area 2 mm^(2) is stretched by 20 N. Find the lateral strain produced in the wire
View SolutionThe equation of a transverse wave along a stretched string is given by
y=15sin2π(t0.04−x40)cm.
The velocity of the wave isView Solution