The harmonic wave yi=(2.0×10−3)cosπ(2.0x−50t) travels along a string towards a boundary at x=0 with a second string. The wave speed on the second string is 50m/s. Write expressions for reflected and transmitted waves. Assume SI units.
The correct Answer is:A, B, C
Speed of wave in first medium is,
v1 = (Coefficient of t)/(Coefficient of x)
= 502=25m/s
v2=50m/s
Ai=2×10−3m.
Ar=(v2−v1v2+v1)Ai=23×(10−3)m
At=(2v2v1+v2)Ai=83×(10−3)m .
In second medium, speed becomes two times. Therefore, λ also becomes two times. So, k remains one-half, value of ω will remain unchanged. Further, second medium is rarer medium (v2>v1). Hence there is no change in phase angle anywhere.
∴yr=23×10−3cosπ(2.0x+50t)
and yt=83×10−3cosπ(2.0x+50t) .
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Assertion And Reason10videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Objective11videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.35videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
- BOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
Similar Questions
A wave yi=0.3cos(2.0x−40t) is travelling along a string toward a boundary at x=0. Write expressions for the reflected waves if .
(a) the string has a fixed end at x=0 and
(b) The string has a free end at x=0.
Assume SI units.View SolutionA harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four times that of the first string, and that the boundary between the two strings is at x=0. If the expression for the incident wave is
yi=Aicos(k1x−ω1t)
(a) What are the expressions for the transmitted and the reflected waves in terms of Ai,k1 and ω1?
(b) Show that the average power carried by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves.View Solution
Knowledge Check
- Question 1 - Select One
A travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string . The juction of the strings is at x=0. The equation of the reflected wave is
Ay'=0.5Asin(kx+ωt+θ)By'=−0.5Asin(kx+ωt+θ)Cy'=−0.5Asin(kx−ωt−θ)Dy'=−0.5Asin(kx+ωt−θ) - Question 2 - Select One
A travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
Ay'=0.5Asin(kx+ωt+θ)By'=−0.5Asin(kx+ωt+θ)Cy'=−0.5Asin(ωt−kx−θ)Dy'=0.5Asin(kx+ωt−θ) - Question 3 - Select One
A wave pulse on a string on a string has the dimension shown in figure. The wave speed is v=1 cm /s . If point O is a free end. The shape of wave at time t = 3s si
 A
A B
B C
C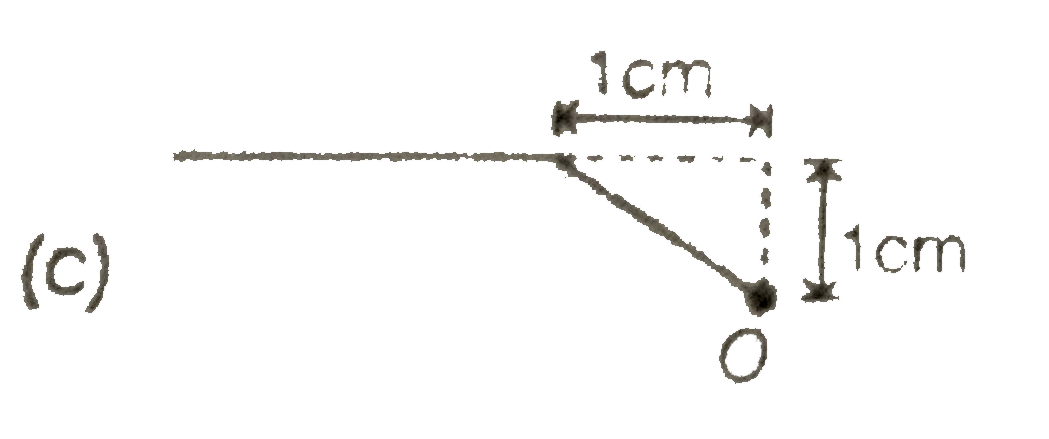 D
D
A harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted . The linear mass density of the second string is four times that of the first string , and that the boundary between the two strings is at x=0 . If the expression for the incident wave is yi=Aicos(k1x−ω1t).
What are the expressions for the transmitted and the reflected waves in terms of Ai,K1andω1?
(b) Show that the average power by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves .View SolutionIf a wave y(x,t)=(5.0 mm) sin(kr +(600 rad/s) t+ϕ) travels along a string, how much time does any given point on the string take to move between displacements y=+2.0 mm and y=-2.0 mm?
View SolutionA harmonic waves is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four time that of the first string. And that the boundry between the two strings is at x=0. If tje expression for the incident wave is, yi=Aicos(k1x−ω1t)
What are the expression for the transmitted and the reflected waves in terms of Ai,k1 and ω1 ?View SolutionA wave travelling along a string is given by y(x,t)=20sin2π(t−0.003x) x, y are in cm and t is in seconds.
Find the amplitude, frequency, wavelength and velocity of the wave.View SolutionThe displacement wave in a string is y=(3cm)sin6.28(0.5x−50t) where x is in centimetres and t in seconds. The velocity and wavelength of the wave is :-
View Solution

