A wave is represented by
$y_{1} = 10 cos (5 x + 25 t)$
where, x is measured in meters and t in seconds. A second wave for which
$y_{2} = 20 cos (5 x + 25 t + \frac{π}{3})$
interferes with the first wave. Deduce the amplitude and phase of the resultant wave.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

$A = \sqrt{{(10)}^{2} + {(20)}^{2} + 2 (10) (20) {cos 60}^{\circ}}$
= 26.46 cm

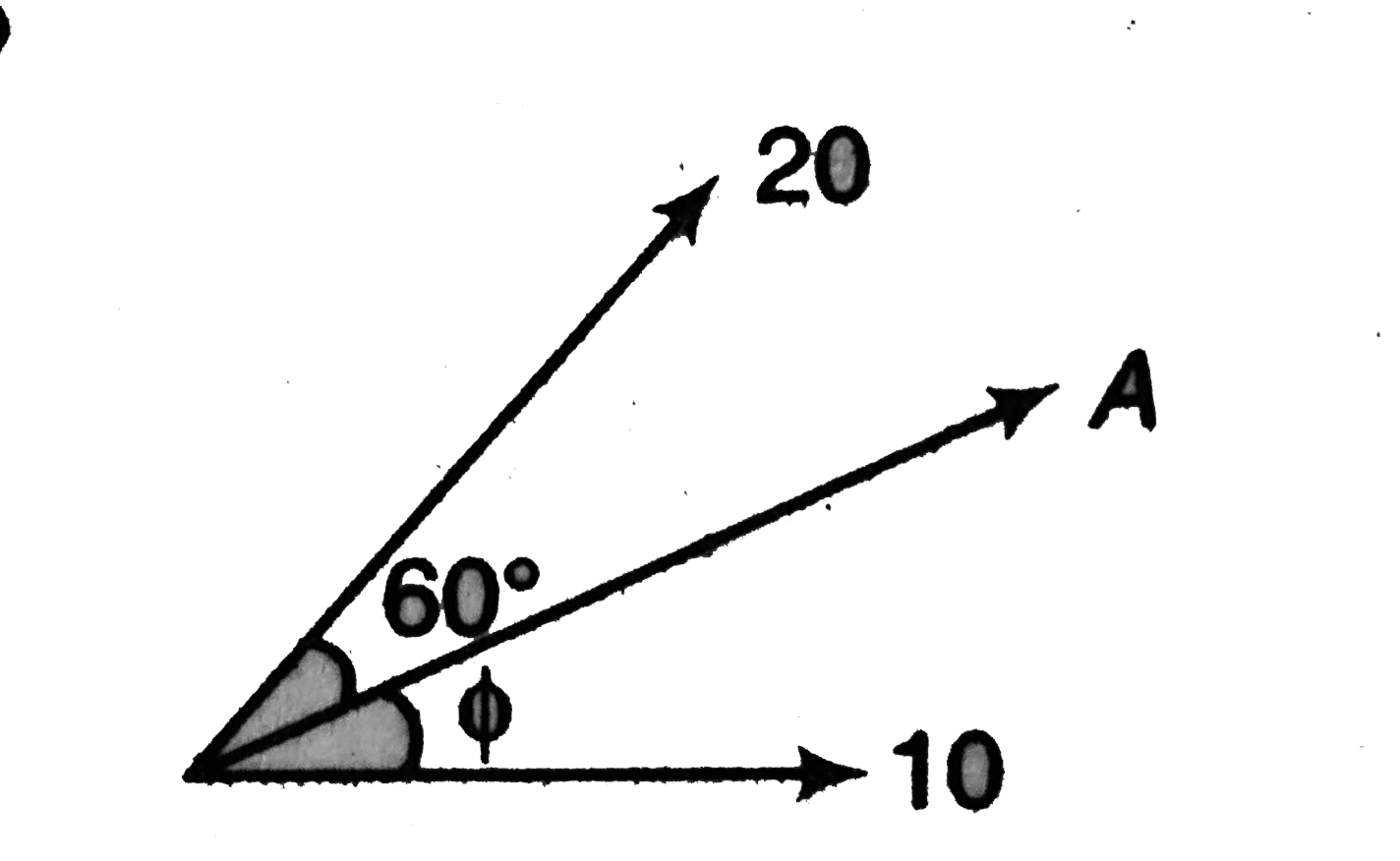
$tan ϕ = \frac{20 {sin 60}^{\circ}}{10 + 20 {cos 60}^{\circ}}$
$= 0.866$
$∴ ϕ = {40.89}^{\circ}$
= $0.714$ rad .

|

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A wave is represented by $y = 0.4 cos (8 t - \frac{x}{2})$ where x and y are in metres and t in seconds. The frequency of the wave is
A $\frac{4}{π} s^{- 1}$
B $\frac{8}{π} s^{- 1}$
C $\frac{5}{π} s^{- 1}$
D $\frac{6}{π} s^{- 1}$
Question 2 - Select One
A wave is represented by the equation, $y = 0.1 sin (60 t + 2 x)$ , where x and y are in metres and t is in seconds. This represents a wave
Atravelling with a speed of $\frac{1}{30}$ m/s, in the negative x direction
Btravelling with a speed of 30 m/s, in the positive x direction
Cof wavelength $30 π$ metre
Dof frequency $(\frac{30}{π})$ hertz
Question 3 - Select One
A wave is represented by the equation $y = 7 sin {π (2 t - 2 x)}$ here x is in metres and t in seconds. The velocity of the wave is
A $1 m / s$
B $2 m / s$
C $5 m / s$
D $10 m / s$

DC PANDEY-SUPERPOSITION OF WAVES-Level 1 Subjective

Home
Ask Doubt
Profile