A wave travels on a light string. The equation of the waves is y=Asin(kx−ωt+30∘). It is reflected from a heavy string tied to an end of the light string at x = 0. If 64% of the incident energy is reflected, then the equation of the reflected wave is
y=0.8Asin(kx−ωt+30∘+180∘)
y=0.8Asin(kx+ωt+30∘+180∘)
y=0.8Asin(kx−ωt−30∘)
y=0.8Asin(kx−ωt+30∘)
The correct Answer is:B
To solve the problem, we need to determine the equation of the reflected wave when a wave traveling on a light string is reflected at the boundary of a heavy string. The given wave equation is:
y=Asin(kx−ωt+30∘)
Step 1: Understand the Reflection of Waves
When a wave travels from a lighter medium to a heavier medium, part of the wave is reflected back. The amplitude of the reflected wave can be determined based on the percentage of energy reflected. The energy reflected is given as 64%.
Step 2: Relate Energy Reflection to Amplitude
The intensity of a wave is proportional to the square of its amplitude. If I is the intensity, then:
I∝A2
If 64% of the energy is reflected, then the intensity of the reflected wave Ir is:
Ir=0.64Ii
Where Ii is the intensity of the incident wave. Therefore, we can express this in terms of amplitudes:
A2rA2i=0.64
Step 3: Calculate the Amplitude of the Reflected Wave
Let Ai be the amplitude of the incident wave and Ar be the amplitude of the reflected wave. Then:
A2r=0.64A2i
Taking the square root gives:
Ar=√0.64Ai=0.8Ai
Step 4: Determine the Phase Change
When a wave reflects off a boundary from a lighter to a heavier medium, it undergoes a phase shift of 180∘ (or π radians). This means we need to adjust the phase of the reflected wave.
Step 5: Write the Equation of the Reflected Wave
The reflected wave travels in the opposite direction, so we replace (kx−ωt) with (kx+ωt) and include the phase shift:
The equation of the reflected wave becomes:
yr=Arsin(kx+ωt+30∘+180∘)
Step 6: Simplify the Equation
Since 180∘ can be added to the phase:
yr=0.8Aisin(kx+ωt+210∘)
Final Answer
Thus, the equation of the reflected wave is:
yr=0.8Asin(kx+ωt+210∘)
When a wave travels from a lighter medium to a heavier medium, part of the wave is reflected back. The amplitude of the reflected wave can be determined based on the percentage of energy reflected. The energy reflected is given as 64%.
The intensity of a wave is proportional to the square of its amplitude. If I is the intensity, then:
Let Ai be the amplitude of the incident wave and Ar be the amplitude of the reflected wave. Then:
When a wave reflects off a boundary from a lighter to a heavier medium, it undergoes a phase shift of 180∘ (or π radians). This means we need to adjust the phase of the reflected wave.
The reflected wave travels in the opposite direction, so we replace (kx−ωt) with (kx+ωt) and include the phase shift:
Since 180∘ can be added to the phase:
Thus, the equation of the reflected wave is:
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 More Than One Correct
6 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - More than One correct Options
1 Video
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Subjective Questions
6 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
Similar Questions
Knowledge Check
A wave travels on a light string. The equation of the wave is Y=Asin(kx−ωt+30∘+180∘). It is relected from a heavy string tied to an end of the light string at x=0. If 64% of the incident energy is reflected the equation of the reflected wave is
AY=0.8Asin(kx−ωt+30∘+180∘)BY=0.8Asin(kx+ωt+30∘+180∘)CY=0.8Asin(kx+ωt−30∘)DY=0.8Asin(kx+ωt+30∘)A travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
Ay'=0.5Asin(kx+ωt+θ)By'=−0.5Asin(kx+ωt+θ)Cy'=−0.5Asin(ωt−kx−θ)Dy'=0.5Asin(kx+ωt−θ)A travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string . The juction of the strings is at x=0. The equation of the reflected wave is
Ay'=0.5Asin(kx+ωt+θ)By'=−0.5Asin(kx+ωt+θ)Cy'=−0.5Asin(kx−ωt−θ)Dy'=−0.5Asin(kx+ωt−θ)
A transverse wave is passing through a light string shown in fig.The equation of wave is y=Asin(wt−kx) the area of cross-section of string A and density is ρ the hanging mass is :
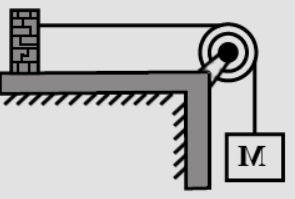
View SolutionA transverse wave is passing through a light string shown in fig.The equation of wave is y=Asin(wt−kx) the area of cross-section of string A and density is ρ the hanging mass is

View SolutionThe equation of a wave travelling on a string is d
View SolutionThe equation of a wave is y=Asin(2πnt)When it is reflected at a free end its amplitude becomes 90% The equation of the reflected wave is
View Solutiontransverse simple harmonic wave is travelling on a string. The equation of the wave:
View Solution
