Sound waves are trqvelling along positive x - direction. Displacement of particle at any time t is as shows in figure. Select the wrong statement.
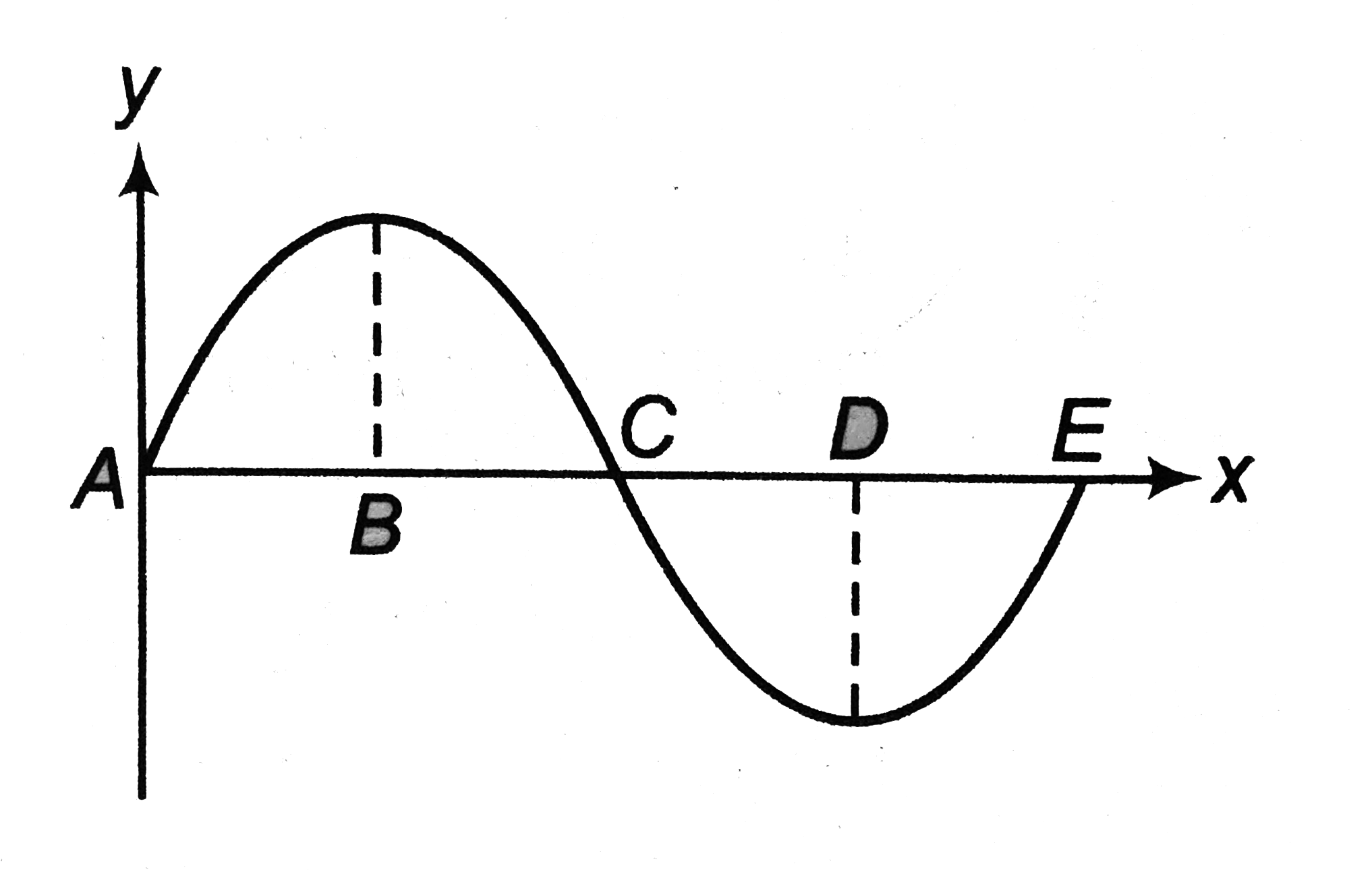
Particle located at E has its velocity in negative x− direction
Particle locted at D has zero velocity
Both (a) and (b) are correct
Both (a) and (b) are wrong
The correct Answer is:C
∴νp=−ν(∂y∂x), where ν=+ ve.
At E , ∂y∂x or slope is positive.
Hence, νp is negative.
At D, ∂y∂x or slope is zero. Hence, νp is zero.
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Single correct option
1 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Level 2 More Than One Correct
5 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Subjective Questions
1 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
Sound wave is travellimg along positive x -direction . Displacement (y) of particles from their mean position at position x is a shown in figure . Choose the correct alternative(s).
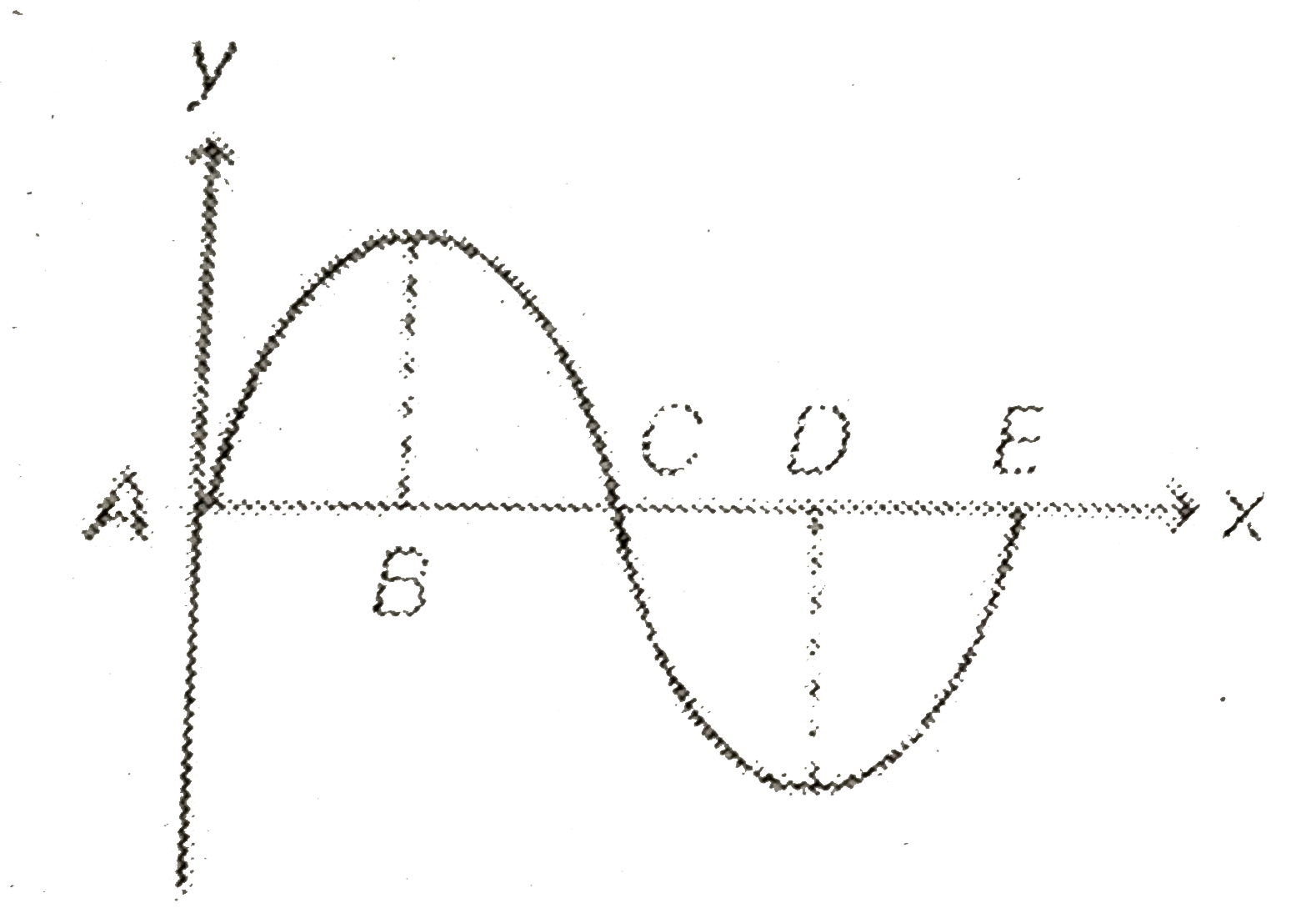
View SolutionA wave pulse is travelling on a string at 2m/s along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
y=2t2+1 Find
Shape of the pulse at t = 0 and t = 1s.
View Solution
Knowledge Check
A long itudinal sine wave is travelling in air along positive x-direction. Displacement(s) of particles from their mean positions at a particular time t are shown in the figure. Choose the correct options for that instant only
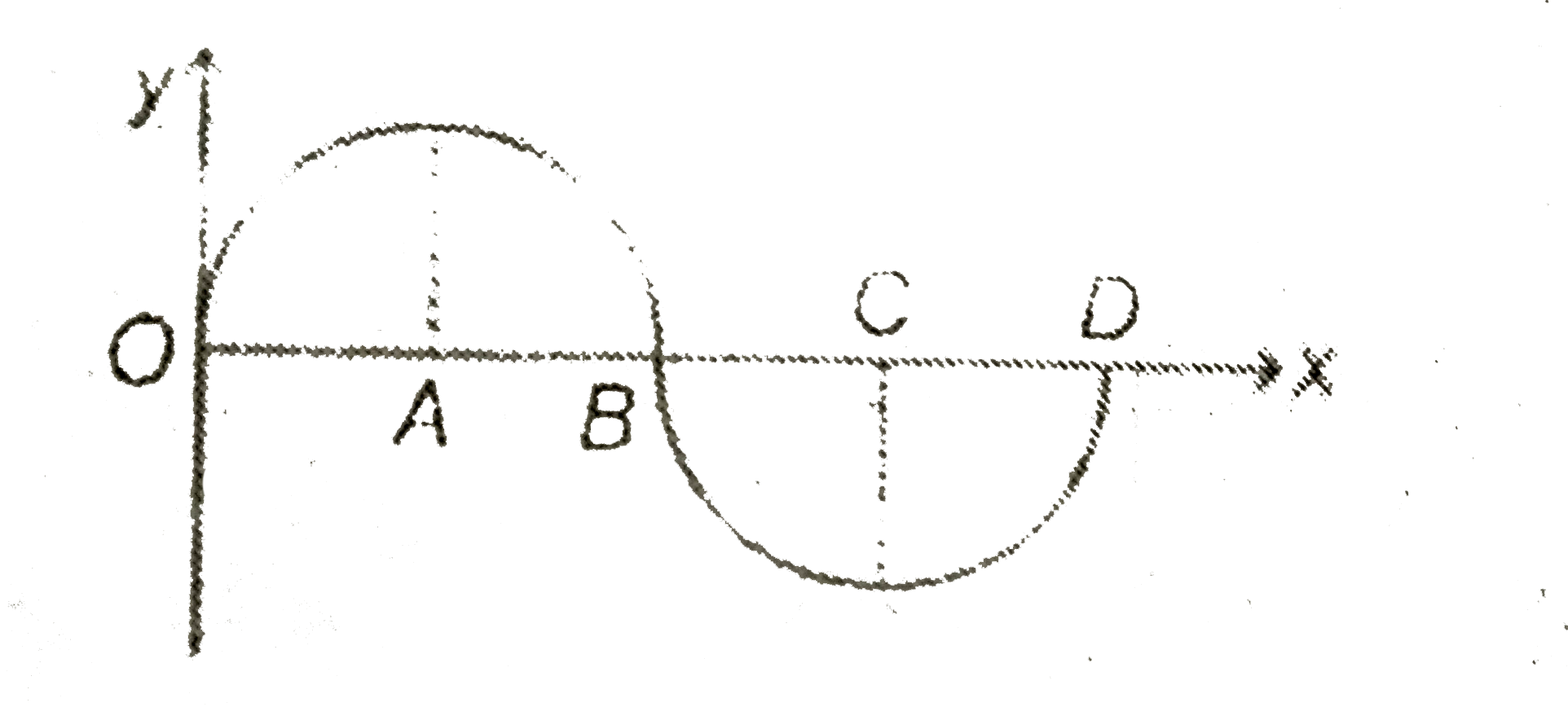 AParticle located at C has zero velocity .BParticle located at C is equal to normal atmospheric directionCThe pressure at C is equal to normal atmospheric pressure .DParticles located near B are under compression.
AParticle located at C has zero velocity .BParticle located at C is equal to normal atmospheric directionCThe pressure at C is equal to normal atmospheric pressure .DParticles located near B are under compression.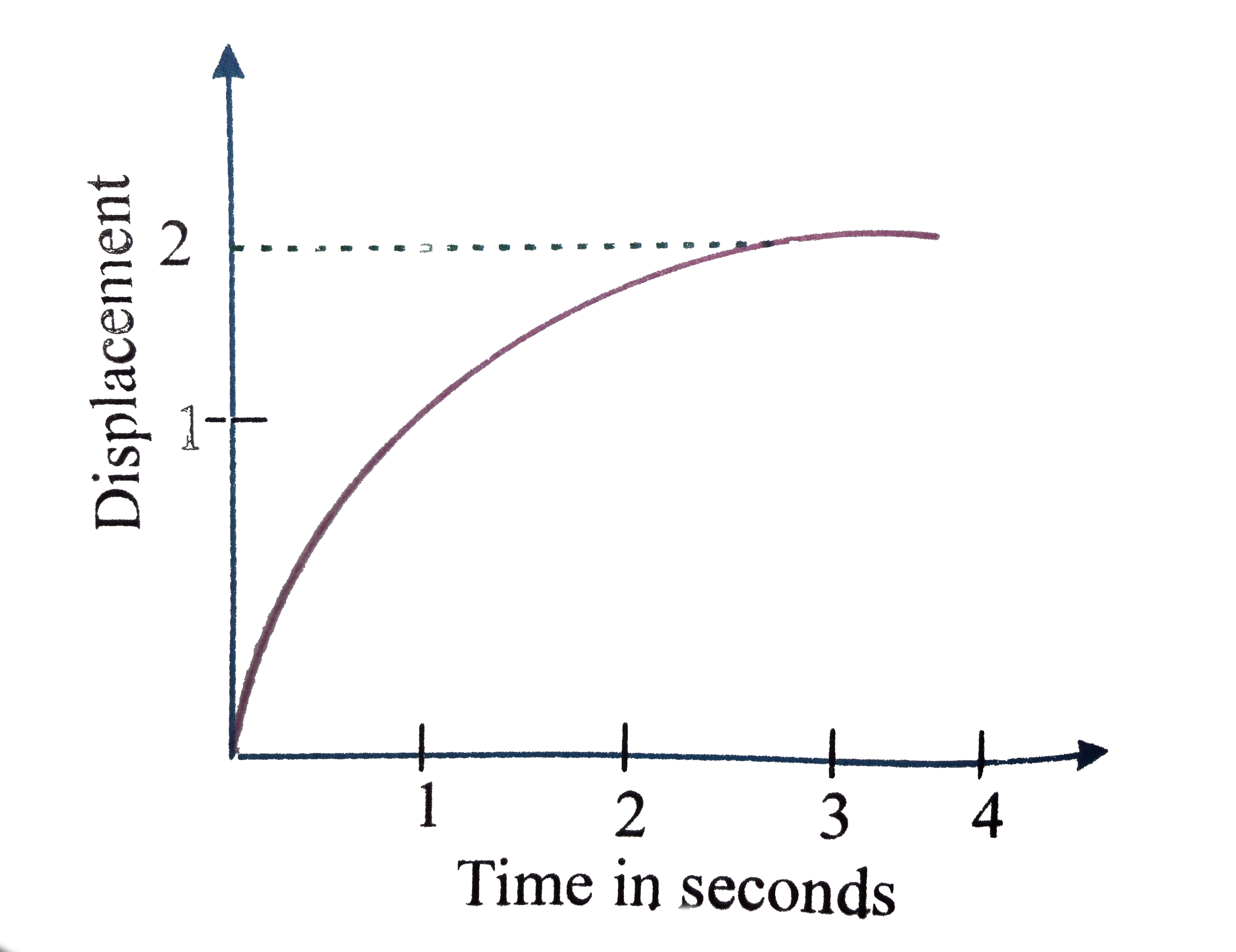
The displacement of a particle as a funtion of time is shown in the figure. The figure shows thatAthe particle starts with certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant through out.Cthe acceleration of the particle is constant throughoutDthe particle starts with constant velocity, the motion is accelerated and finally the particle move with another constant velocity.The displacement of a particle as a function of time is shown in the figure. The figure shows that
 Athe particle starts with certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant through outCthe acceleration of the particle is constant throughoutDthe particle starts with constant velocity, then motion is accelerated and finally the particle moves with another constant velocity.
Athe particle starts with certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant through outCthe acceleration of the particle is constant throughoutDthe particle starts with constant velocity, then motion is accelerated and finally the particle moves with another constant velocity.
A sinusoidal wave having wavelength of 6m propagates along positive x direction on a string. The displacement (y) of a particle at x=2m varies with time (t) as shown in the graph
(a) Write the equation of the wave
(b) Draw y versus x graph for the wave at t=0

View Solution(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.

View SolutionA simple harmonic wave of amplitude "2mm" is travelling along positive x-axis.At a given instant, displacement for two different particles on the wave is 1mm and √2mm along positive Y direction.If wave length of wave is 48mm then find minimum separation between positions of the particles (in mm)
View SolutionA wave pulse is travelling along +x direction on a string at 2m/s. Displacement y (in cm ) of the parrticle at x=0 at any time t is given by 2/(t2+1). Find
(i) expression of the function y=(x,t),i.e., displacement of a particle at position x and time t.
Draw the shape of the pulse at t=0 and t=1 s.
View SolutionStatement-1: A string of length 4 m is vibrating in its fourth overtone. The wavelength of the wave is 80 cm.
Statement-2: Doppler's effect is applicable only when source or observer moves with constant speed.
Statement-3: For a wave travelling along positive x-axis the displacement of a particle x at time t is same as that of the particle at origin at time (t-xlv) where v is the wave speed.
View Solution
