A piece of metal floats on mercury. The coefficient of volume expansion of metal and mercury are γ1andγ2, respectively. if the temperature of both mercury and metal are increased by an amount ΔT, by what factor does the frection of the volume of the metal submerged in mercury changes ?
The correct Answer is:A, B, D
fi=ρsρl⇒fi=ρ′sρ′l
∴f′ifi=(ρ′sρs)(ρlρ′l)=(1+γlΔT1+γsΔT)=(1+γ2ΔT1+γ1ΔT)
Now, 11+γ1ΔT≈(1−γ1ΔT)
∴f′ifi=(1+γ2ΔT)(1−γ1ΔT)
Neglecting γ1γ2(ΔT)2 term, we get
f′ifi≈(γ2−γ1)ΔT
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Exercise 20.37videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEYCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Exercise 20.43videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEYCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Exercise 20.15videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEYCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason2videos
UNIT AND DIMENSIONS
Similar Questions
A piece of metal floats on mercury. The coefficients of volume expansion of the metal and mercury are γ1 and γ2 respectively. If the temperatures of both mercury and the metal are increased by an amount ΔT, the fraction of the volume of the metal submerged in mercury changes by the factor............
View SolutionBy what factor does the capacity of a metal sphere increase if its volume is tripied ?
View Solution
Knowledge Check
- Question 1 - Select One
A glass container of volume V contains some mercury. The coefficients of cubical expansion for glass and mercury are γg and γm , respectively. If the volume of air inside the flask remains constant at different temperature, then the volume of mercury in the flask is
AγmVγgBγgVγmC(1−γmγg)VD(1−γgγm)V - Question 2 - Select One
State true/false:
S1 : Hydrostatic pressure is a scalar quantity even though pressure is force divided by area and force is a vector quantity?
S2: A barometer made of a very narrow tube (see figure) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018/.∘C and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C but the temperature of the atmosphere does not change. Then, the mercury height in the tube remains unchanged.
S3 A block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
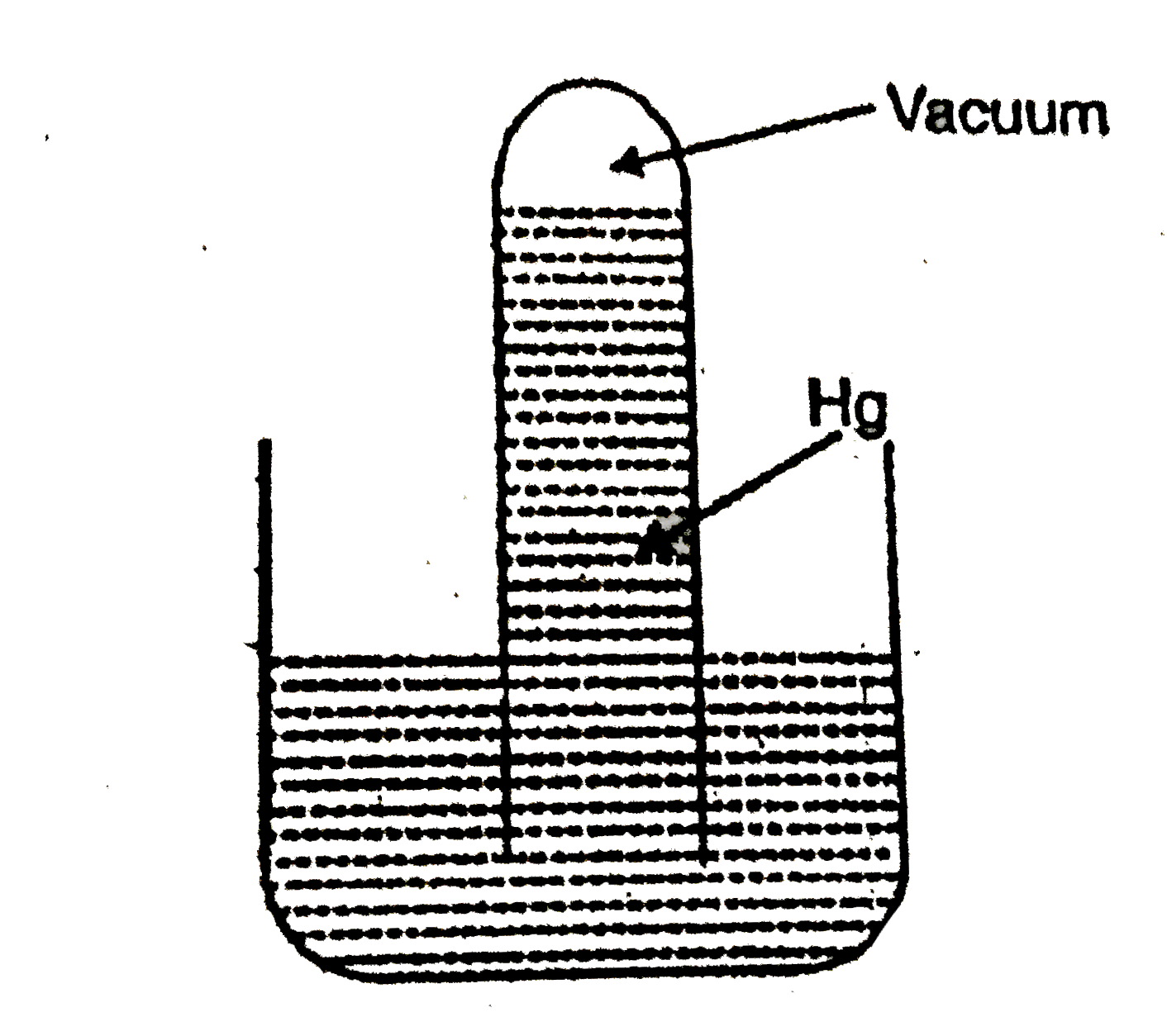 ATTFBTFTCTFFDTTT
ATTFBTFTCTFFDTTT - Question 3 - Select One
The radious of a metal sphere at room temperature T is R, and the coefficient of linar expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
A2πRαΔTBπR2αΔTC4πR3αΔt/3D4πR3αΔT
A barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
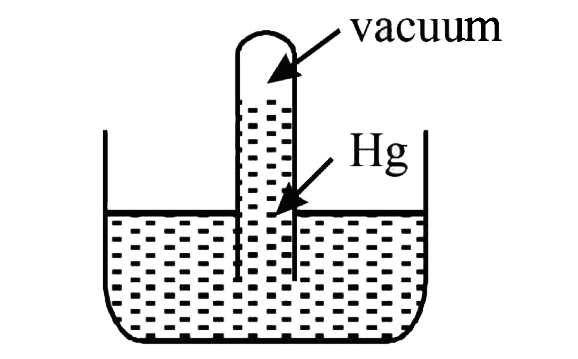 View Solution
View SolutionIn a cylidrical glass container a solid silica is placed vertically at its bottom and remaining space is filled with mercury upto the top level of the silica. The volume of silica remains unchanged with variation in temperature. The coefficient of cubical expansion of mercury is γ and coefficient of linear expansion of glass is α. If the top surface of silica and mercury level remain at the same level wiht the variation in temperature then the ratio of volume of silica tothe volume of mercury is equal:
 View Solution
View Solutionthe coefficient of volume expansion of mercury is 20times the linear expansion of glass. Find the volume of mercury that must be poured in to glass vessel of volume V so that the volume above the mercury remain constant at all temperatures
View SolutionEach side of a box made of metal sheet in cubic shape is 'a' at room temperature 'T', the coefficient of linear expansion of the metal sheet is 'α'. The metal sheet is heated uniformly, by a small temperature ΔT , so that its new temperature is T+ΔT . Calculate the increase in the volume of the metal box.
View SolutionThe radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
View Solution

