Show that the volume thermal expansion coefficient for an ideal gas at constant pressure is 1T.
The correct Answer is:A
To show that the volume thermal expansion coefficient (γ) for an ideal gas at constant pressure is 1T, we can follow these steps:
Step 1: Define the volume thermal expansion coefficient
The volume thermal expansion coefficient (γ) is defined as:
γ=ΔVVΔT
where ΔV is the change in volume, V is the original volume, and ΔT is the change in temperature.
Step 2: Use the ideal gas law
For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by the ideal gas equation:
PV=nRT
where n is the number of moles and R is the ideal gas constant.
Step 3: Differentiate the ideal gas equation
At constant pressure, we can differentiate the ideal gas equation with respect to temperature:
PdVdT=nR
This implies:
dVdT=nRP
Step 4: Substitute nR using the ideal gas law
From the ideal gas law, we know that nR=PVT. Substituting this into the equation we derived in Step 3 gives:
dVdT=PVPT=VT
Step 5: Relate ΔV to ΔT
Now, we can express ΔV in terms of ΔT:
ΔV=VTΔT
Step 6: Substitute ΔV back into the definition of γ
Now, substituting ΔV into the definition of γ:
γ=ΔVVΔT=VTΔTVΔT=1T
Conclusion
Thus, we have shown that the volume thermal expansion coefficient for an ideal gas at constant pressure is:
γ=1T
---
The volume thermal expansion coefficient (γ) is defined as:
γ=ΔVVΔT
where ΔV is the change in volume, V is the original volume, and ΔT is the change in temperature.
For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by the ideal gas equation:
PV=nRT
where n is the number of moles and R is the ideal gas constant.
At constant pressure, we can differentiate the ideal gas equation with respect to temperature:
PdVdT=nR
This implies:
dVdT=nRP
From the ideal gas law, we know that nR=PVT. Substituting this into the equation we derived in Step 3 gives:
dVdT=PVPT=VT
Now, we can express ΔV in terms of ΔT:
ΔV=VTΔT
Now, substituting ΔV into the definition of γ:
γ=ΔVVΔT=VTΔTVΔT=1T
Thus, we have shown that the volume thermal expansion coefficient for an ideal gas at constant pressure is:
γ=1T
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct7videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEYCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason2videos
UNIT AND DIMENSIONS
Similar Questions
Prove that the coefficient of cubical expansion of an ideal gas at constant pressure is equal to the reciprocal of its absolute temperature.
View SolutionCalculate the ΔH for the isothermal reversible expansion of 1 mole of an ideal gas from initial pressure of 0.1¯ at a constant temperature at 273K.
View Solution
Knowledge Check
- Question 1 - Select One
If an ideal gas is heated at constant pressure :
Athe volume increasesBthe mass of gas remains sameCthe kinetic energy of the molecules increasesDattraction forces between gas particles increases - Question 2 - Select One
Work done during expansion of an ideal gas against constant opposing pressure is given by
AW=2.303 RT log V2V1BW=2.303 RT log V1V2CW=−P(V2−V1)DW=0 - Question 3 - Select One
The volume-temperature graphs of a given mass of an ideal gas at constant pressure are shown below. What is the correct order of pressure ?
 AP1>P3>P2BP1>P2>P3CP2>P3>P1DP2>P1>P3
AP1>P3>P2BP1>P2>P3CP2>P3>P1DP2>P1>P3
The volume-temperature graphs of a given mass of an ideal gas at constant pressures are shown below. What is the correct order of pressures ?
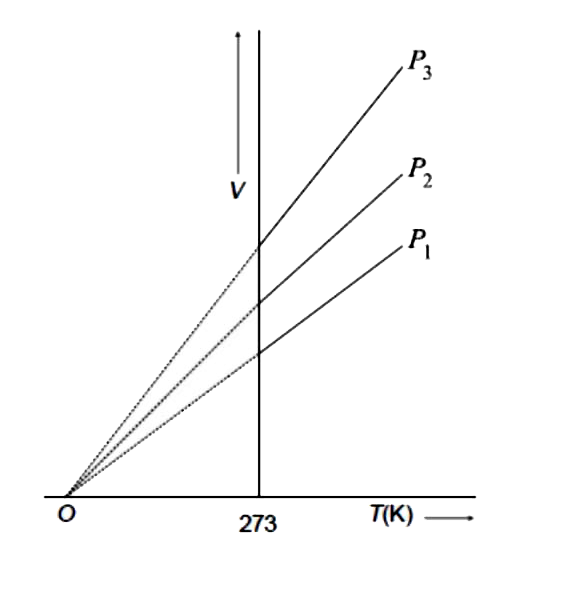 View Solution
View SolutionThermal coefficient of volume expansion at constant pressure for an ideal gas sample of n moles having pressure P0, volume V0, and temperature T0 is
View SolutionWhat will be the work done for expansion of a gas from 1 lit to 10 lit volume agaist constant pressure of 1 bar?
View SolutionFor an ideal gas PT11 = constant then volume expansion coefficient is equal to :-
View SolutionThe expansion of an ideal gas of mass ma t a constant pressur p is given by the straight line B. Then, the expansion of the same ideal gas of mass 2m at a pressure 2p is goven by the straight line.
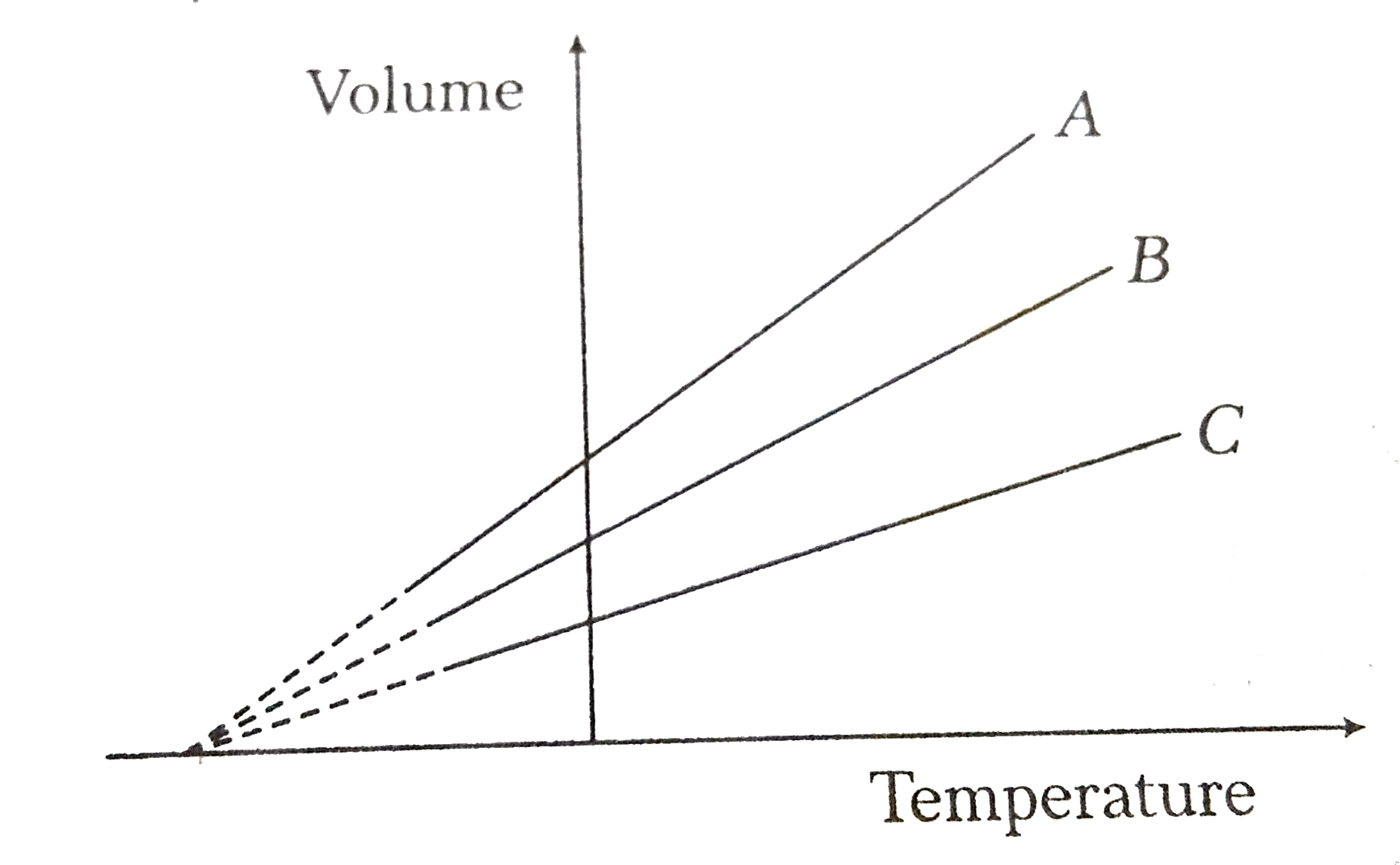 View Solution
View Solution

