The ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
The correct Answer is:A, B, C, D
To solve the problem of finding the temperature gradient in the two halves of a copper rod with a heat source in the center, we will follow these steps:
Step 1: Understand the setup
We have a copper rod of length L=1m and cross-sectional area A=1cm2=1×10−4m2. The ends of the rod are maintained at temperatures T1=0∘C and T2=100∘C. There is a heat source in the center of the rod that provides power P=25W.
Step 2: Calculate the total temperature difference
The total temperature difference across the rod is given by:
ΔT=T2−T1=100∘C−0∘C=100K
Step 3: Calculate the heat transfer in steady state
In steady state, the heat transfer through the rod can be described by Fourier's law of heat conduction:
P=k⋅A⋅ΔTL
where k is the thermal conductivity of copper, k=400Wm−1K−1.
Step 4: Calculate the temperature gradient
We can rearrange the formula to find the temperature gradient ΔTL:
ΔTL=Pk⋅A
Substituting the known values:
ΔTL=25W400Wm−1K−1⋅1×10−4m2
Calculating this gives:
ΔTL=25400×1×10−4=250.04=625K/m
Step 5: Determine the temperature gradient in each half
Since the heat source is at the center, the rod is divided into two halves. The temperature gradient in each half can be considered uniform. Therefore, the temperature gradient in each half of the rod is:
Temperature Gradient=625K/m2=312.5K/m
Final Answer
The temperature gradient in the two halves of the rod in steady state is 312.5K/m.
---
We have a copper rod of length L=1m and cross-sectional area A=1cm2=1×10−4m2. The ends of the rod are maintained at temperatures T1=0∘C and T2=100∘C. There is a heat source in the center of the rod that provides power P=25W.
The total temperature difference across the rod is given by:
ΔT=T2−T1=100∘C−0∘C=100K
In steady state, the heat transfer through the rod can be described by Fourier's law of heat conduction:
P=k⋅A⋅ΔTL
where k is the thermal conductivity of copper, k=400Wm−1K−1.
We can rearrange the formula to find the temperature gradient ΔTL:
ΔTL=Pk⋅A
Substituting the known values:
ΔTL=25W400Wm−1K−1⋅1×10−4m2
ΔTL=25400×1×10−4=250.04=625K/m
Since the heat source is at the center, the rod is divided into two halves. The temperature gradient in each half can be considered uniform. Therefore, the temperature gradient in each half of the rod is:
Temperature Gradient=625K/m2=312.5K/m
The temperature gradient in the two halves of the rod in steady state is 312.5K/m.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Single Correct
7 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct
5 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Objective
11 Videos
- BASIC MATHEMATICSBOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
One end of a copper rod of length 1 m and area of cross - section 400×(10−4)m2 is maintained at 100∘C. At the other end of the rod ice is kept at 0∘C. Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, KCu=401W/m−KandLf=3.35×(105)J/kg.
View SolutionThe lleft end of a copper rod (≤n>h=20cm.Areaofcrosssection=0.02cm2 is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any lkkoss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm=−1^(@)C^(-1) .
View Solution
Knowledge Check
The ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK
 AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/mTwo ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
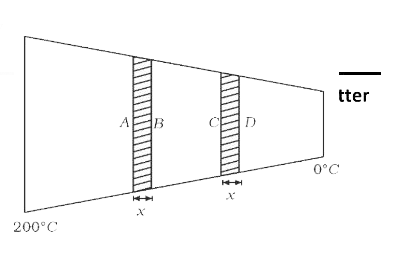 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.Two ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:
 Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Two rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

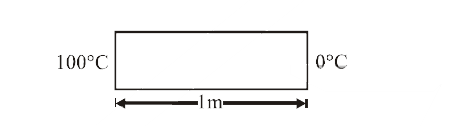
View SolutionA rod of 1 m length and area of cross-section 1cm2 is connected across two heat reservoirs at temperatures 100∘Cand0∘C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod = 0.09 kilocal m−1s−1(∘C)]
View SolutionOne end of a copper rod of length 0.25m and area of cross-section 10−4m2 is immersed in a liquid boiling at 125∘C whereas the other end is kept cold by dipping It in an ice-cold bath. Find (i) temperature gradient, (ii) the rate of heat transfer (iii) the temperature at a point 0.1m from the higher temperature end. (λ of copper =92cals−1m−1K−1)
View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
View SolutionThe heat is flowing through a rod of length 50 cm and area of cross-section 5cm2 . Its ends are respectively at 25∘C and 125∘C . The coefficient of thermal conductivity of the material of the rod is 0.092kcal/m×s×.∘C . The temperature gradient in the rod is
View Solution
