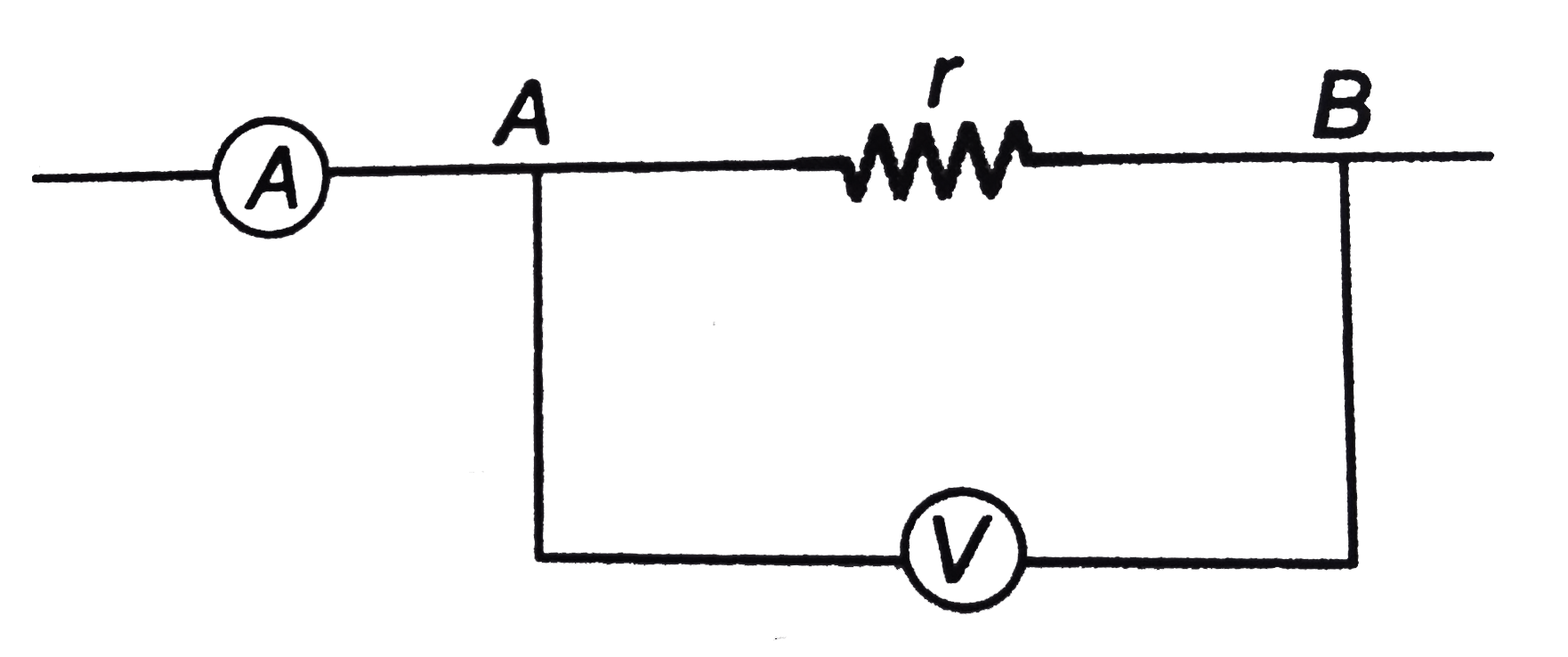
Determine the resistance r if an ammeter shows a current of I=5A and a voltmeter 100V. The internal resistance of the voltmeter is R=2,500Ω
The correct Answer is:B
Current through voltmeter

=VR=1002500=0.04A
In parallel current distribution in inverse ratio of resistors. Hence
4.960.04=2500r
∴r=20.16Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Single Correct
26 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 More Than One Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE_TYPE
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
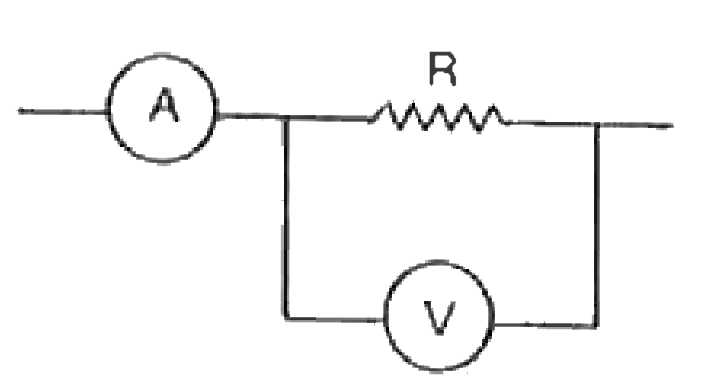
The circuit shown here is used to measure resitance R. An ammeter shows a current of 2A and a voltmeter of a potential difference of 120 V. what is the resitance R if the internal resistance of the voltmeter is Rv = 3000Ω?
How large will the error in measuring R be, if the resistance of the voltmeter is assumed to be infinitely large?
View SolutionIn given figure an ammeter reads 5 A and voltmeter reads 40 V. The actual value of resistance R is

View Solution
Knowledge Check
In the circuit shown below, the ammeter A reads 5 A and the voltmeter V reads 20 V The correct value of resistance R is
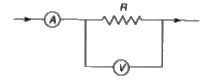 Aexactlt 4Ω.Bslightly greater than 4ΩCslightly less than 4ΩDzero
Aexactlt 4Ω.Bslightly greater than 4ΩCslightly less than 4ΩDzeroThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
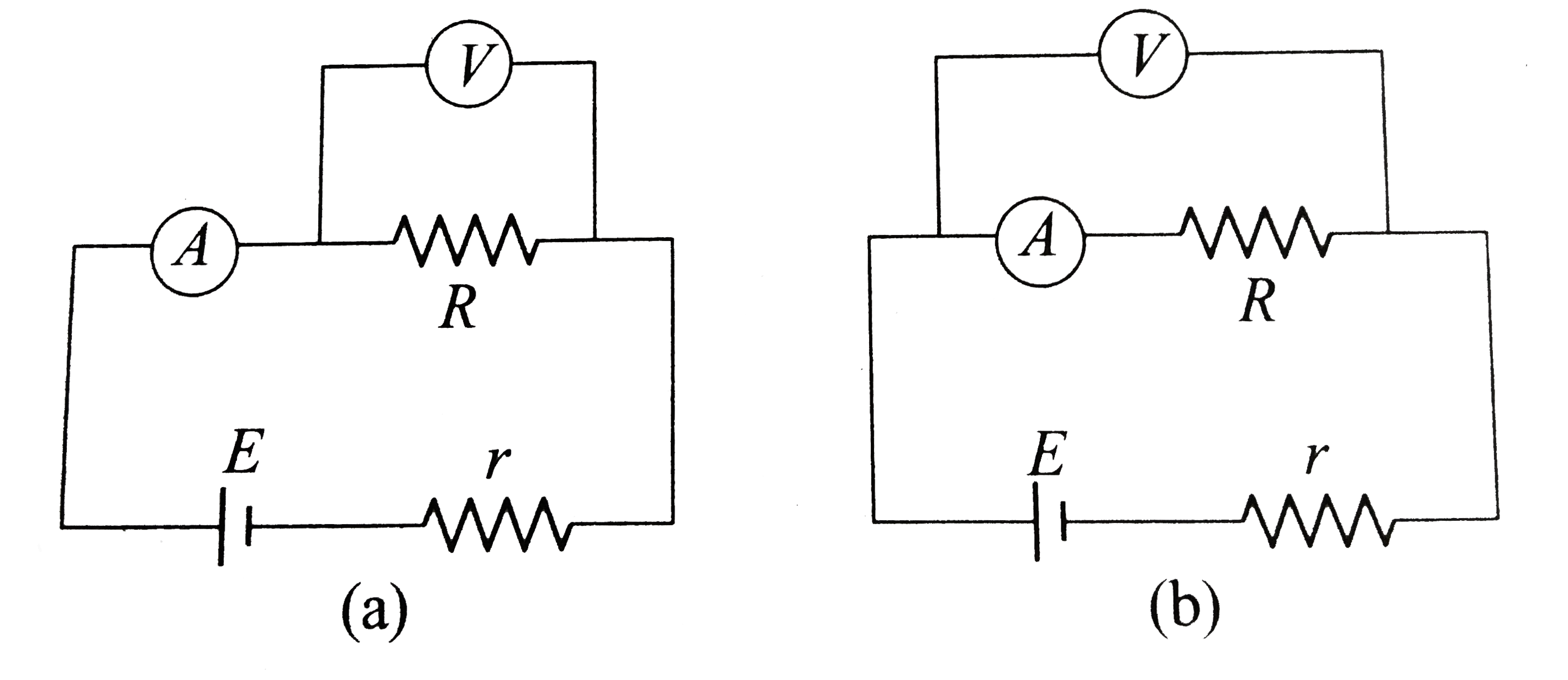 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)isAzero in both casesBnonzero but equal in both casesCmore in circuit ADmore in circuit B
The actual value of resistance R, shown in the figure is 30Ω. This is measured in an experiment as shown using the standard formula R=VI, where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5% less, then the internal resistance of the voltmeter is
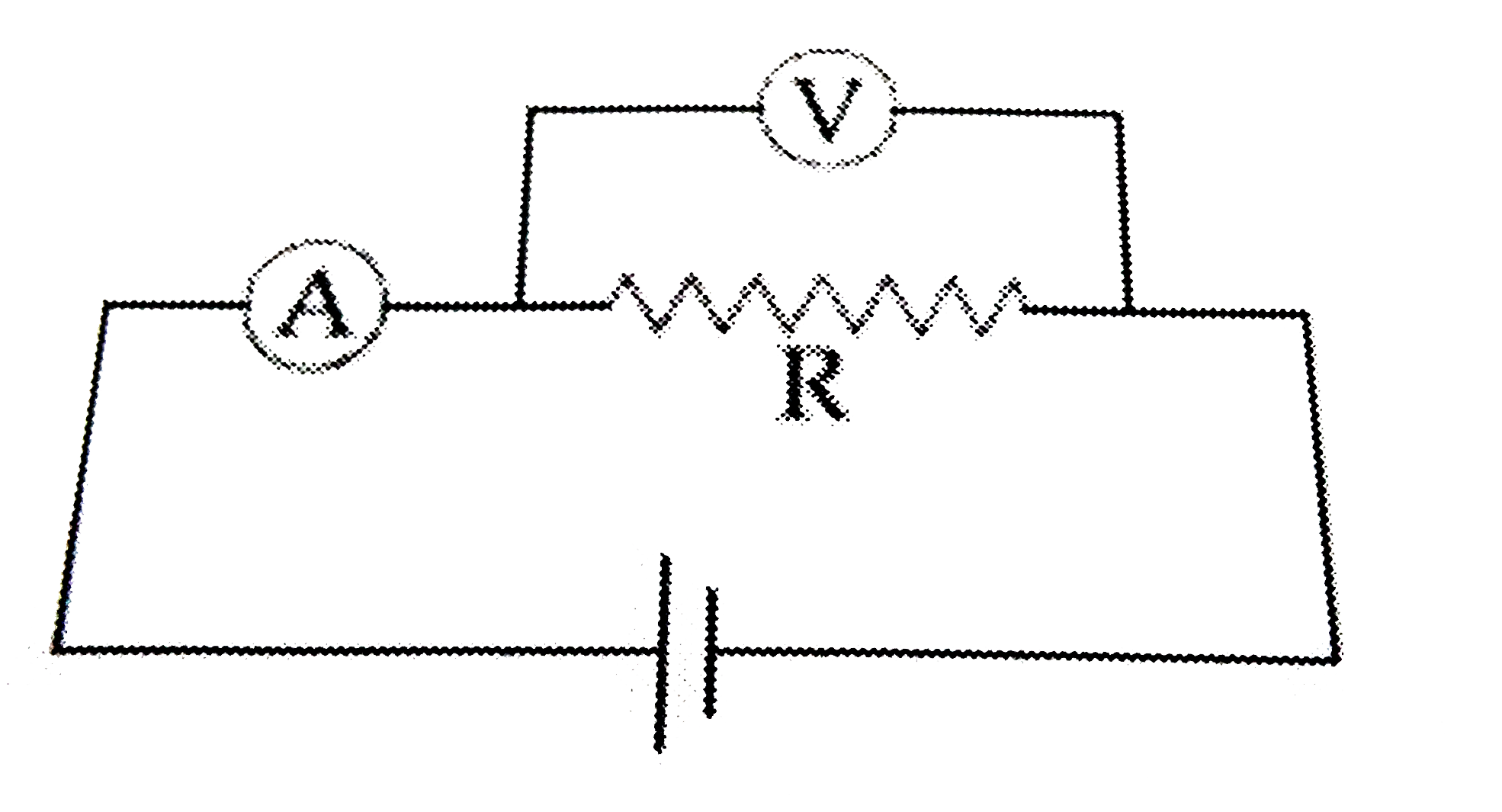
View SolutionIn given figure the ammeter A reads 5 A and voltmeter V reads 40 V. The actual value of resistance R is
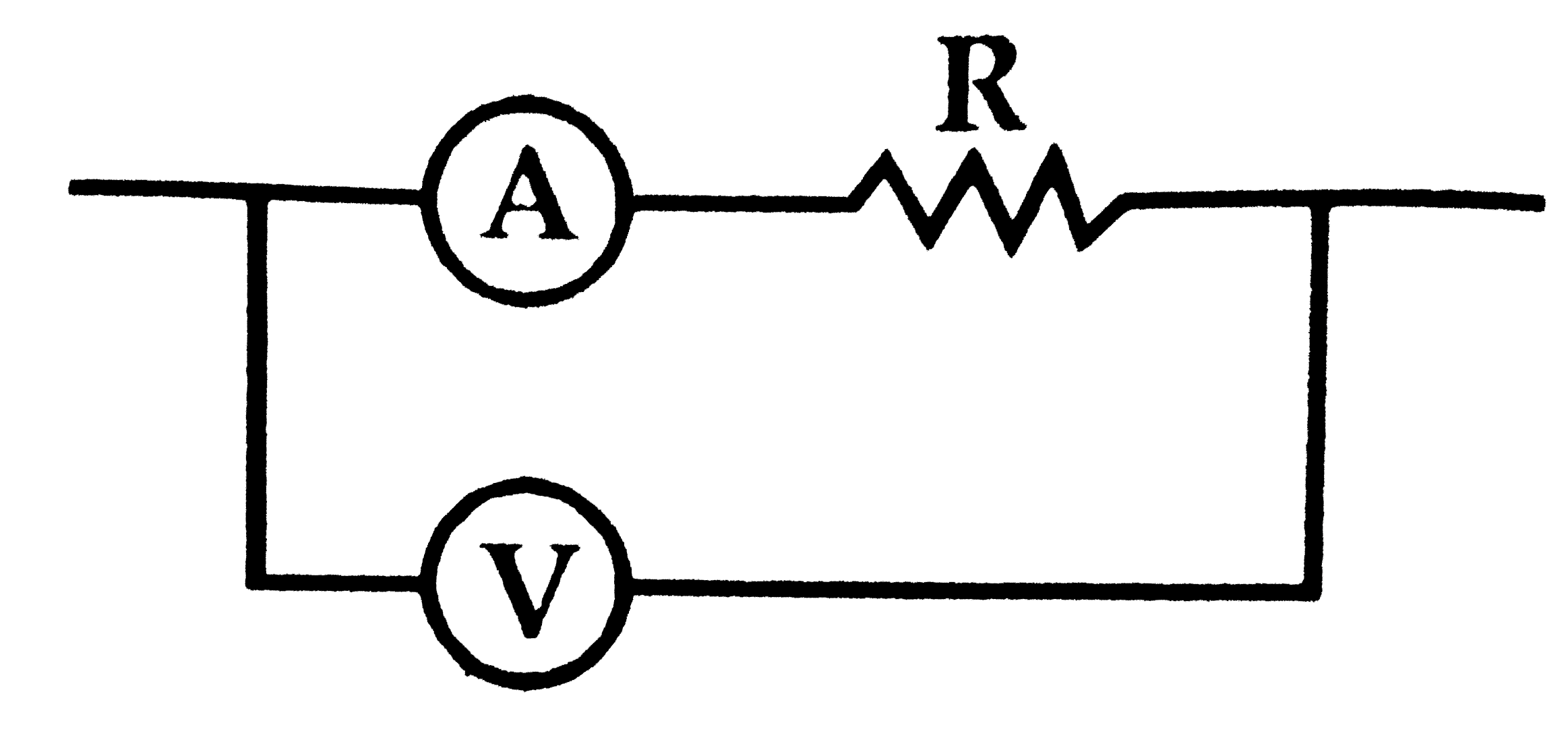
View SolutionIn the adjacent circuit the ammeter reads 5.0 A and voltmeter reads 20V. The value of resistance R is

View SolutionIf the resistance R1 is increased how will the reading of the ammeter and voltmeter change
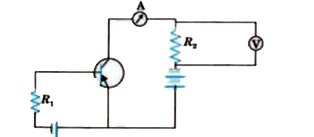
View SolutionThe voltmeter V in the figure. Reads 117V and the ammeter A reads 0⋅13A. The resistance of the voltmeter is 9000Ω and the resistance of ammeter is 0⋅015Ω. Compute (i) the resistance R, (ii) the power input to R.
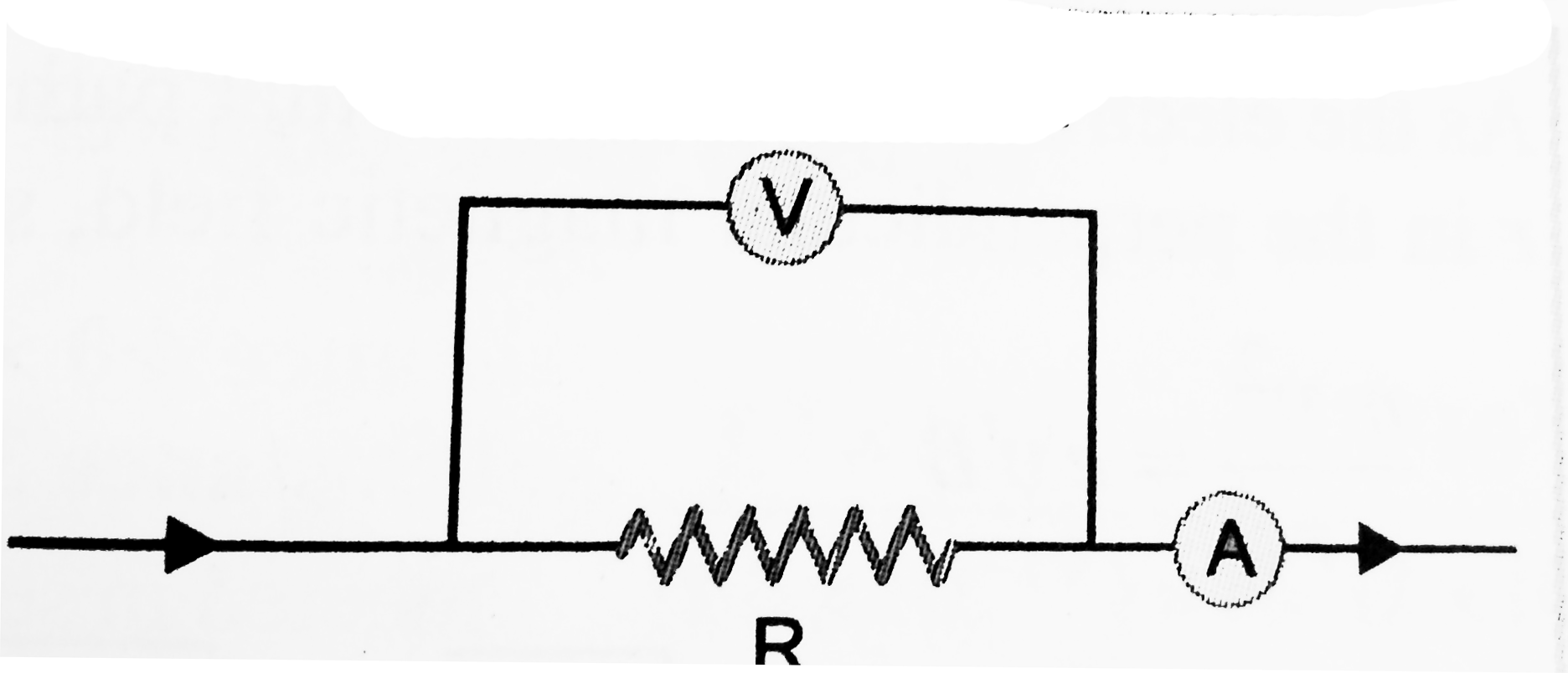
View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.

Let RvandRG be the calculated values in the two cases A and B respectively.
If the resistance of voltmeter is Rv=1kΩ and that of ammeter is RG=1Ω the magnitude of the percentage error in the measurement of R (the value of R is nearly 10Ω ) is:
View Solution
