In a circuit shown in figure if the internal resistances of the sources are negligible then at what value of resistance R will the thermal power generated in it will be the maximum. What is the value of maximum power?
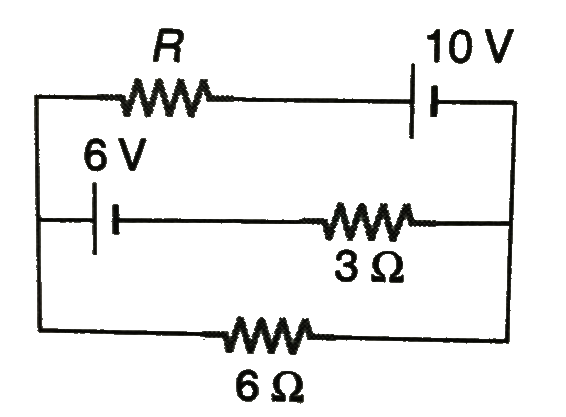
The correct Answer is:A, B, D
Applying Kirchhoff's laws in two loops we have

10−i1R−6+3i2=0 …………i
6−6(i1+i2)−3i2=0…………ii
Solving these two equations we get
i1=6R+2
Power developed in R
P=i21R=36(R+2)2............iii
For power to be maximum,
dPdR=0
∴(R+2)2(36)−(36R)(2)(R+2)=0
orR+2−2R=0
∴R=2Ω
From maximum power from eqn iii we have
Pmax=4.5W
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
61 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type
2 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In a circuit shown in figure if the internal resistance of the sources are negligible then at what value of resistance R will the thermal power generated in it be the maximum. What is its value in ohms ?
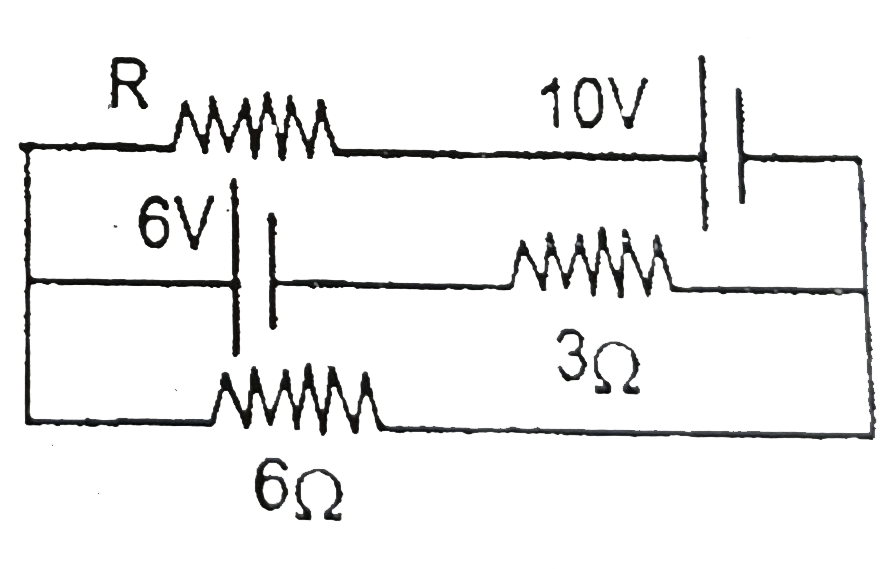
View SolutionIn the given circuit if the internal resistance of the batteries are negligible, then for what value of resistance R(inΩ) will the thermal power generated in it be maximum.

View Solution
Knowledge Check
In the circuit shown in figure, power generated in
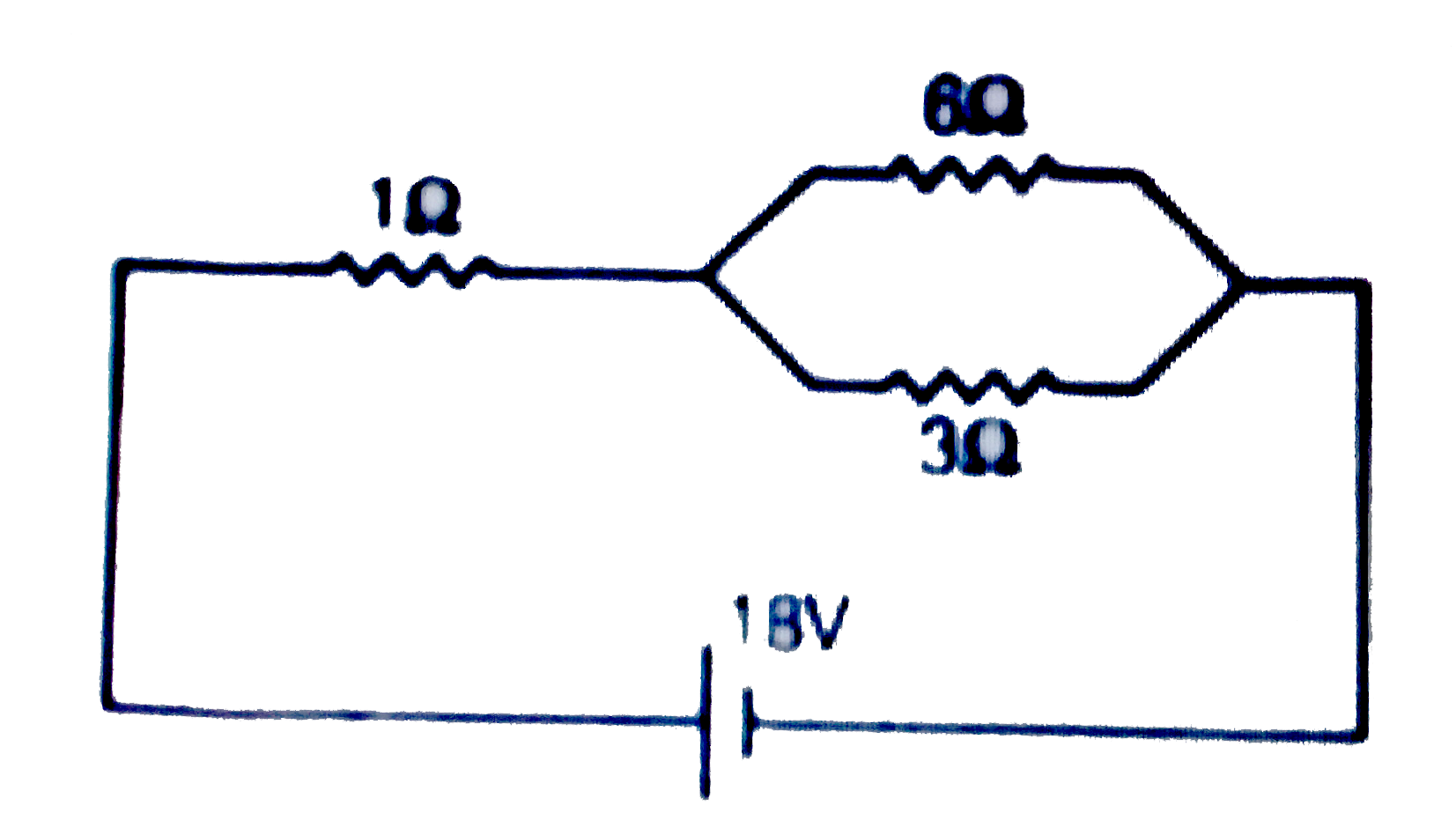 A1Ω resistance is maximumB3Ω resistance is maximumC1Ω resistance is minimumD6Ω resistance is minimum
A1Ω resistance is maximumB3Ω resistance is maximumC1Ω resistance is minimumD6Ω resistance is minimumIn the given circuit, the valuue of R so that thermal power generated in R will be maximum is:
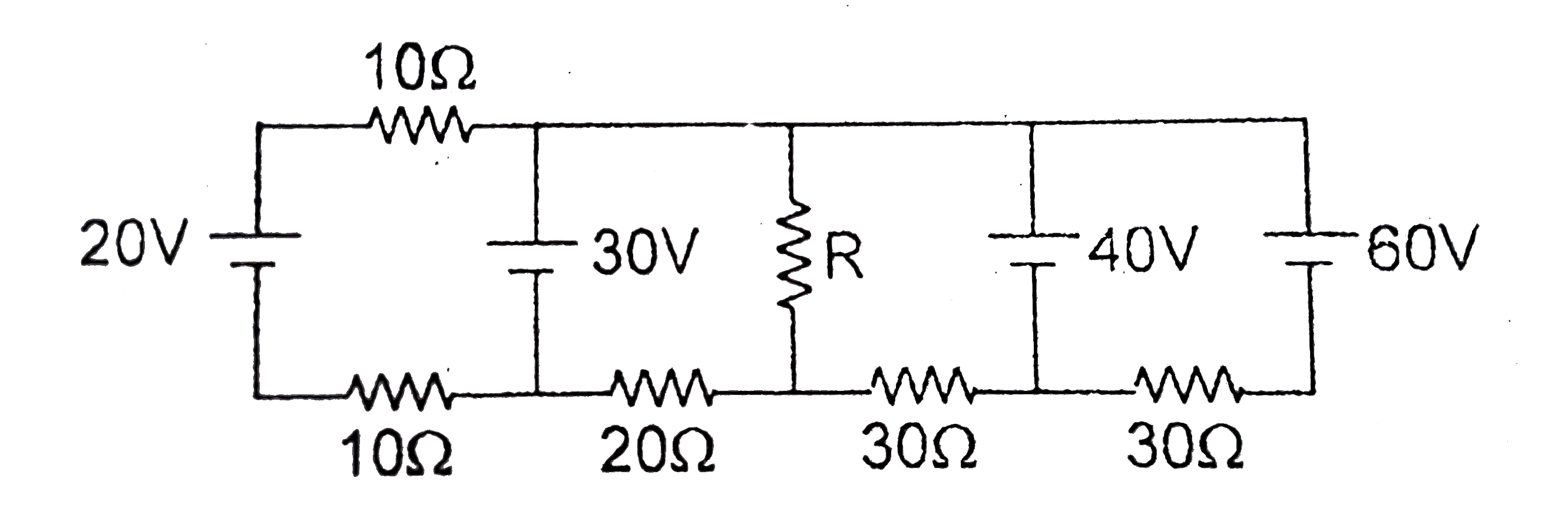 A10ΩB12ΩC8ΩD6Ω
A10ΩB12ΩC8ΩD6Ω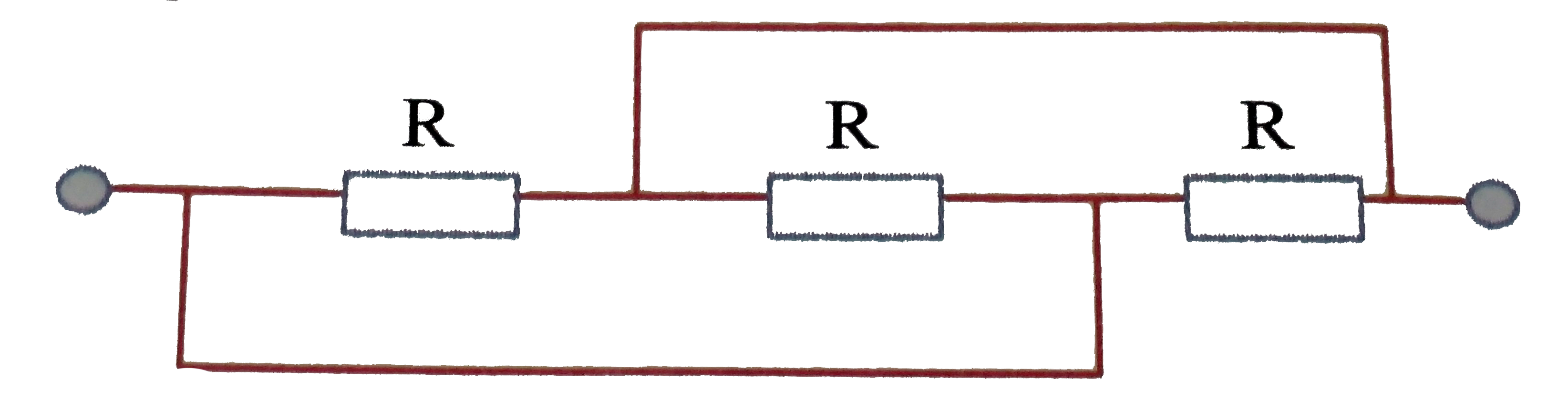
A dc source with internal resistance R0 is loaded with three identical resistance R as shown in the figure. At what value of R will the thermal power generated in this circuit be the highest?AR=2R0BR=3R0CR=R03DR=R0
In a circuit shown in Fig, resistances R1 and R2 are known , as well as emf's ξ1 and ξ2. The internal resitances of the sources are negatible. At what value of the resitance R will teh thermal power generated in it be the highest ? What is it equal to ?
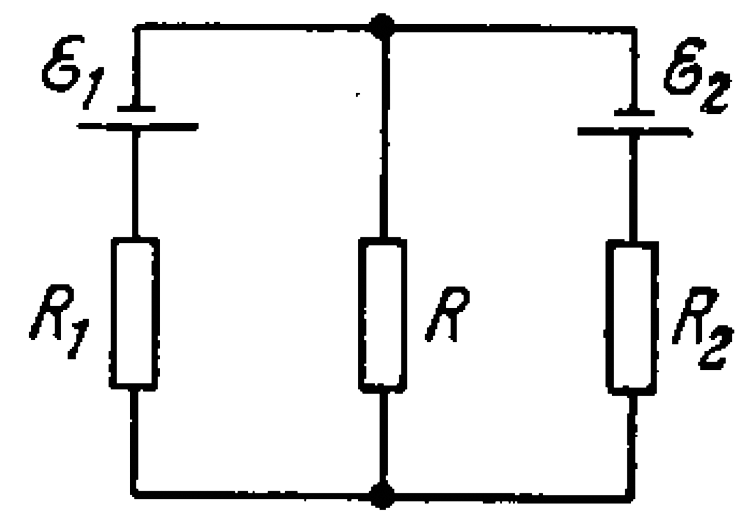
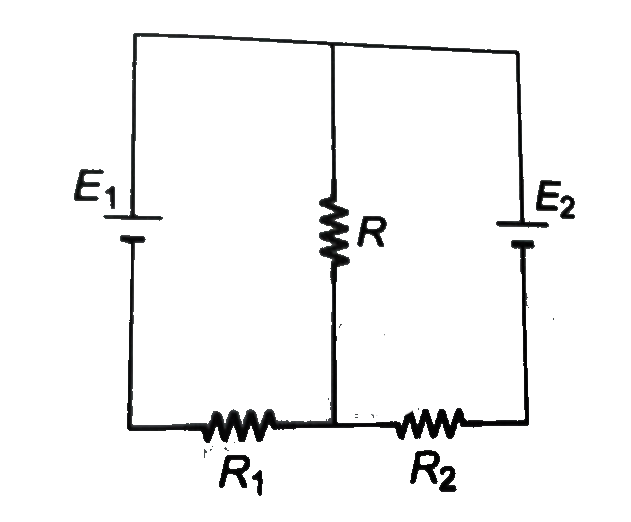
View SolutionIn the circuit shown in figure, the emfs of batteries are E1, and E2 which have internal resistances R1, and R2. At what value of the resistance R will the thermal power generated in it be the highest? What it is?
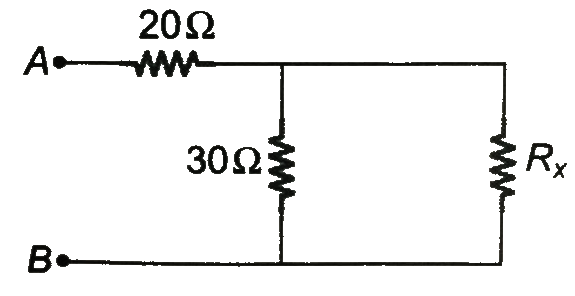
View SolutionA circuit shown in the figure has resistances 20Ω and 30Ω. At what value of resistance Rx will the thermal power generated in it be practically independent of small variations of that resistance? The voltage between points A and B is supposed to be constant in this case.
View SolutionIn the circuit shown in figure-3.196, find the value of resistance ?R at which the power transferred to this resistance will be maximum.
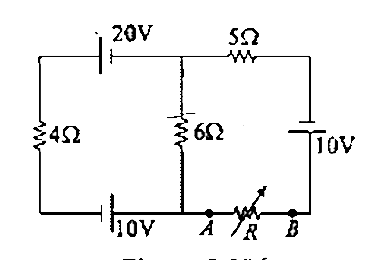
View SolutionFor maximum power from battery the internal resistance of battery r is
View Solution
