Two identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
zero
q(Q1−Q2)(√2−1)√2(4πε0R)
q√2(Q1+Q2)(4πε0R)
q(Q1Q2)(√2+1)√2(4πε0R)
The correct Answer is:B
VC1=VQ1+VQ2=14πε0Q1R+14πε0Q2R√2=14πε0R(Q1+Q2√2) 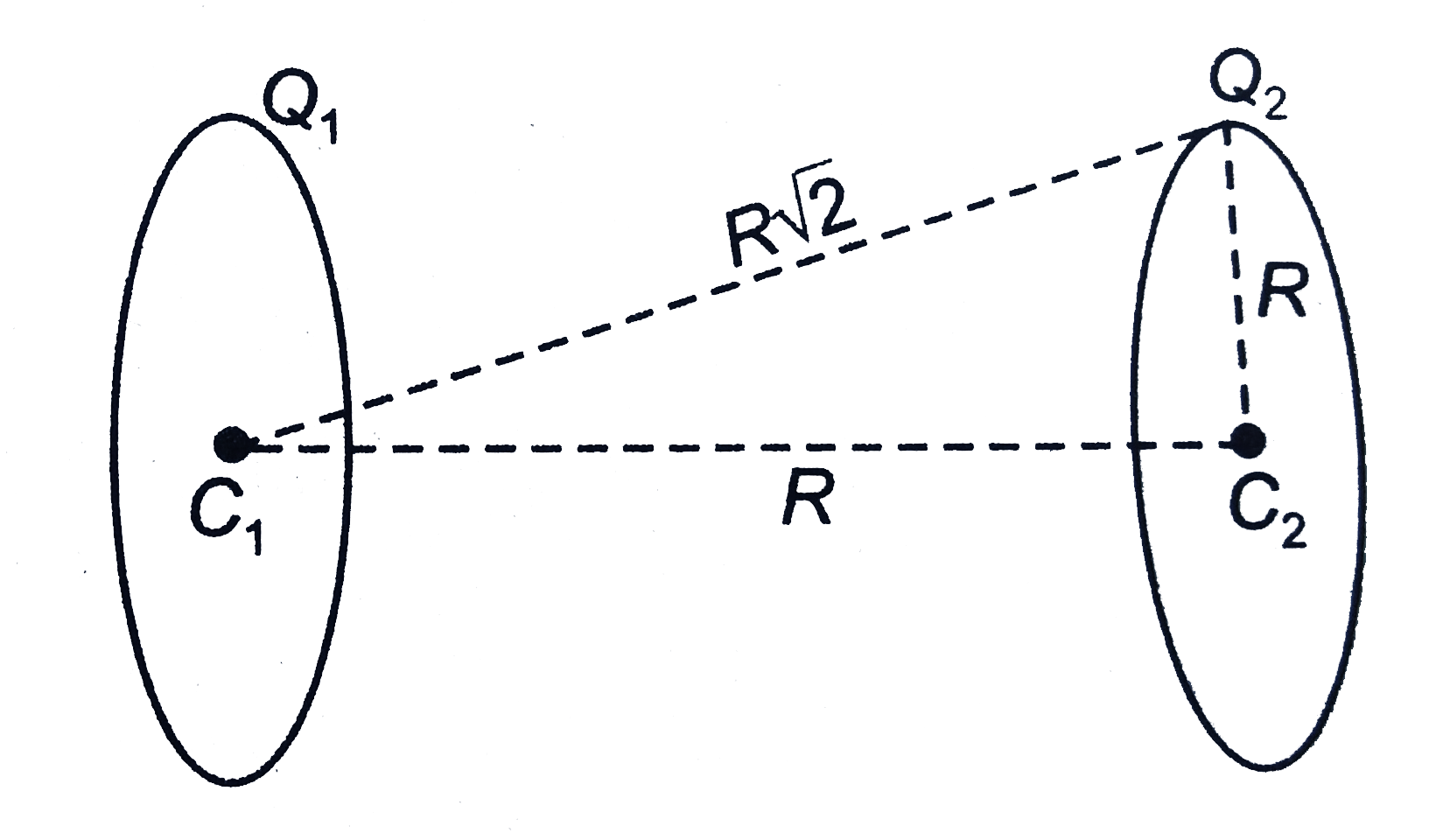
Similarly VC214πε0R(Q2+Q1√2)
∴ΔV=VC1−VC2
=14πε0R[(Q1−Q2)−1√2(Q1−Q2)]
=Q1−Q2√2(4πε0R)(√2−1)
W=q△V=q(Q1−Q2)√2−1√2(4πε0R)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Two identical thin rings, each of radius R, are coaxially placed a distance R apart. Q1 and Q2 are respectively the charges uniformly spread on the two rings. The work done in moving a charge q fróm the centre of one ring to that of the other is (√x−y)q(Q2−Q1)4√2πɛ0R. Find (x−y)
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View Solution
Knowledge Check
Two identical thin ring each of radius R are co-axially placed at a distance R. If the ring have a uniform mass distribution and each has mass m1 and m2 respectively, then the work done in moving a mass m from the centre of one ring to that of the other is :
AzeroBGm(m1−m2)(√2−1)√2RCGm√2(m1+m2)RDGm1m(√2+1)m2RTwo identical thin rings each of radius R are coaxially placed at a distance R. If the rings have a uniform mass distribution and each has masses 2m and 4m respectively, then the work done in moving a mass m from centre of one ring to that of the other is
AzeroB√2Gm2R(1−√2)CGm2√2R(√2−1)DGm2√2RTwo identicaln thin rings each of radius 10 cm carrying charges 10 C and 5 C are coaxially placed at a distance 10 cm apart. The work done in moving a charge q from the centre of the first ring to that of the second is
Aq8πε0.[√2+1√2]Bq8πε0.[−√2+1√2]Cq4πε0.[√2+1√2]Dq4πε0.[√2−1√2]
Two identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA positive charge Q is uniformly distrubuted along a circular ring of radius R.a small test chage q is placed at the centre of the ring .The

View SolutionA charge Q is uniformly distributed only on the fourths portion of a ring of radius R. The elctric potential at centre of ring is
View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
View Solution
