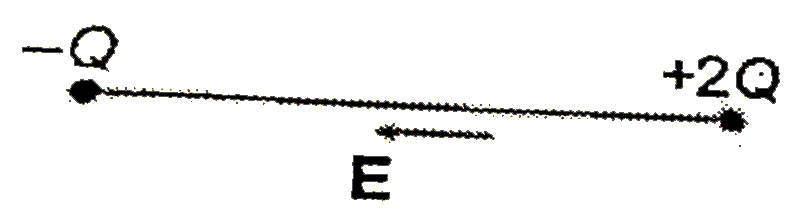
Charge 2qand−q are placed at (a,0)and(−a,0) as shown in the figure. The coordinates of the point at which electric field intensity is zero will be (x,0) where

A
−a<x<a
B
x<−a
C
x>−a
D
0<x<a
Video Solution
Text Solution
The correct Answer is:B
Between 2q and −q, two electric fields are in same direction. So their resultant can't be zero. To the right of 2q left of -q they are in opposite directions. So net field will be zero nearer to charge having small magnitude.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason19videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions120videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
Charges +2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be
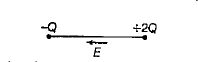 ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q
ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q - Question 2 - Select One
Two charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
Ar(1+√3) from 3e chargeBr(1+√3) from e chargeCr(1−√3) from 3e chargeDr1+√13 from e charge - Question 3 - Select One
Two charge 9e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is :
A(r1+√3) from 9e chargeB(r1+√1/3) from 9e chargeC(r1−√3) from 3e chargeD(r1+√1/3) from 3e charge
Two charges q1andq2 are placed at (0,0d)and(0,0−d) respectively. Find locus of points where the potential is zero.
View SolutionIn the diagram shown electric field intensity will be zero at a point.
 View Solution
View SolutionTwo identical charge of value Q each are placed at (-a,0) and (a , 0) . The end coordinates of the point where the net electric field is zero and maximum are respectively-
View SolutionTwo point charges+q nd -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
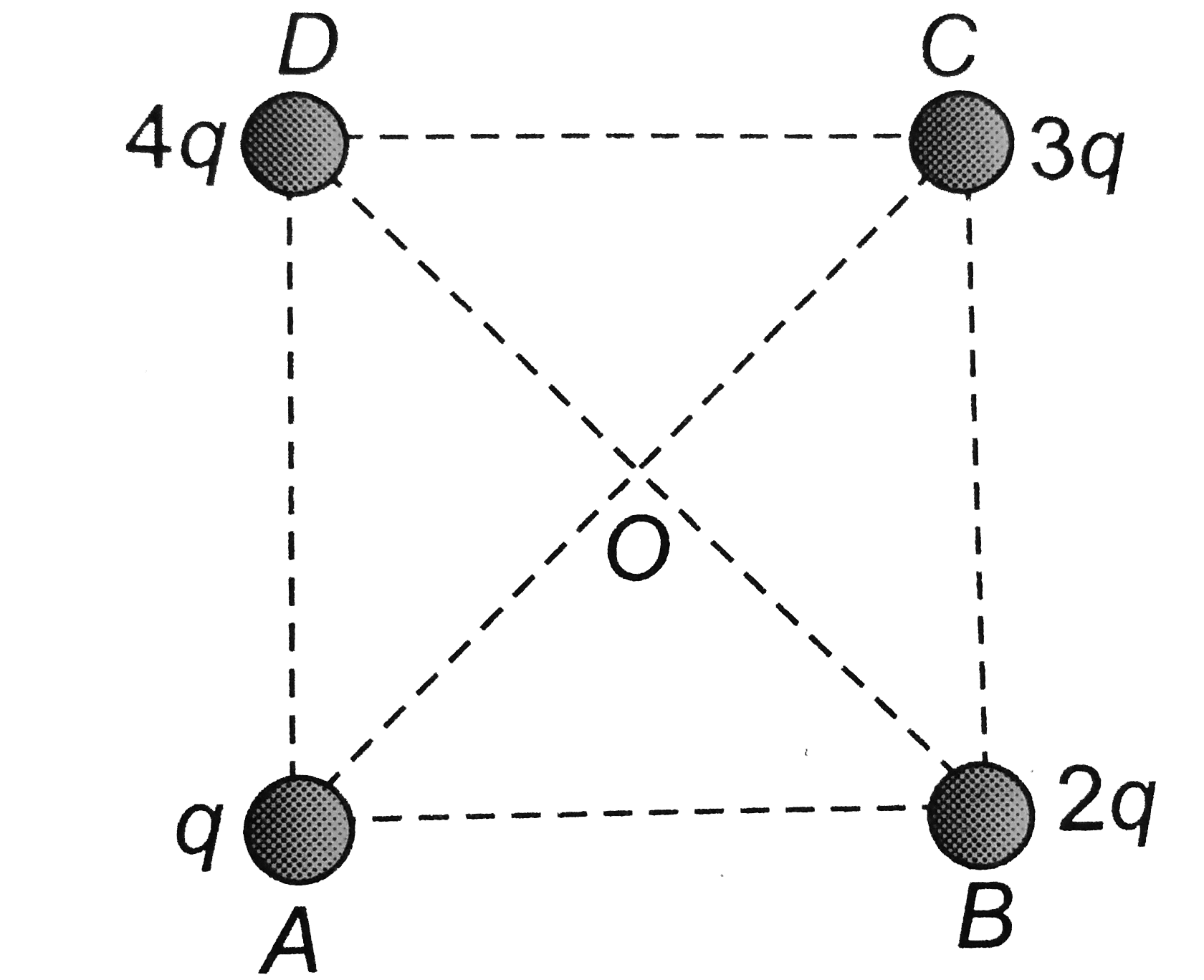
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
 View Solution
View Solution