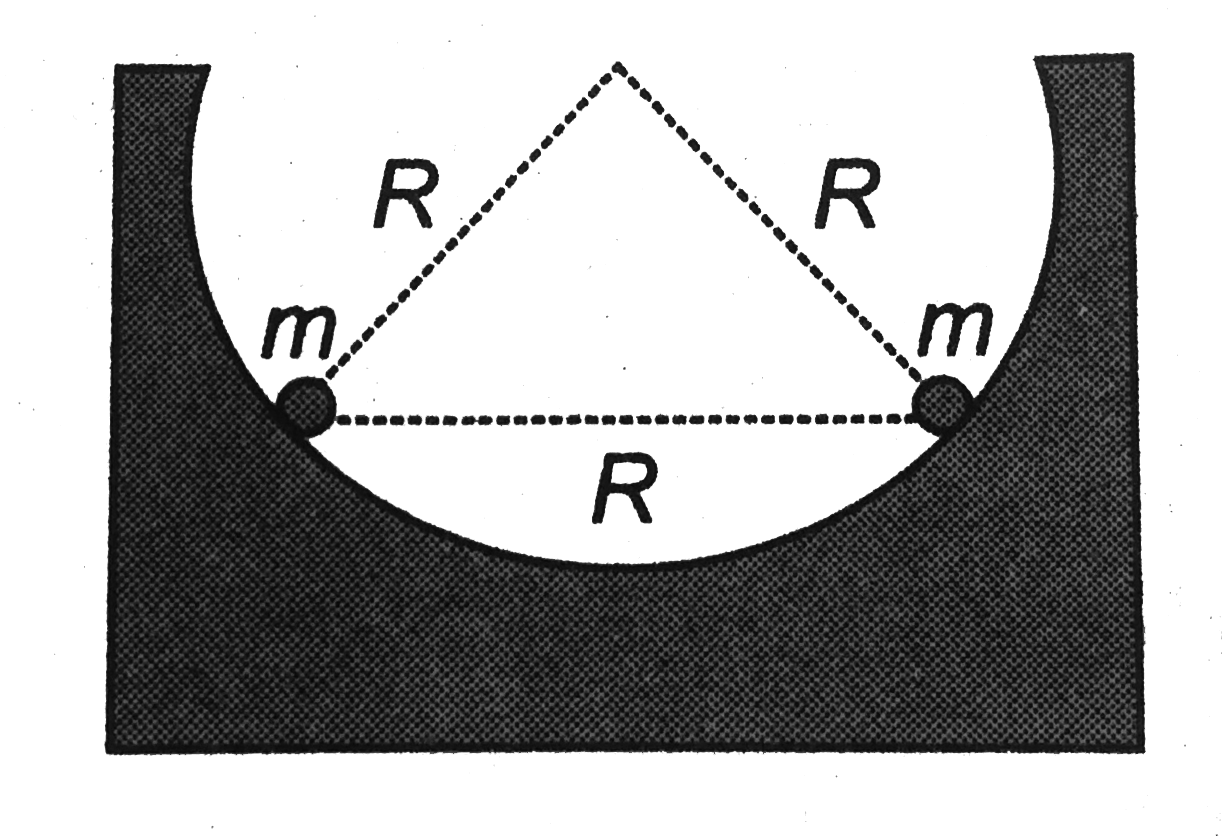
Two identical beads each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, non-conducting walls, the beads move, and at equilibrium they area distance R apart (figure). Determine the charge on each bead.
The correct Answer is:A, B, C, D

Using Lami's theorem we have
mgsin(90∘+30∘)=mgsin(90∘+60∘)
∴F=mg√3or14πε0(q)(q)R2=mg√3
∴Q=√πε0mgR2√3
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Two point charges, each of mass m and charge q are released when they are at a distance from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionTwo identical metal spheres A and B have equal and similar charges. They repel each other with a force 103N, when they are placed 10cm apart in a medium of dielectric constant 7. Determine the charge on each sphere.
View Solution
Knowledge Check
Two identical small balls each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, nonconductive walls, the bead move, and at equilibrium the line joining the balls is horizontal and the distance between them is R (see figure). Neglect any induced charge on the hemispherical bowl. Then the charge on each bead is : (here K=14πε0)
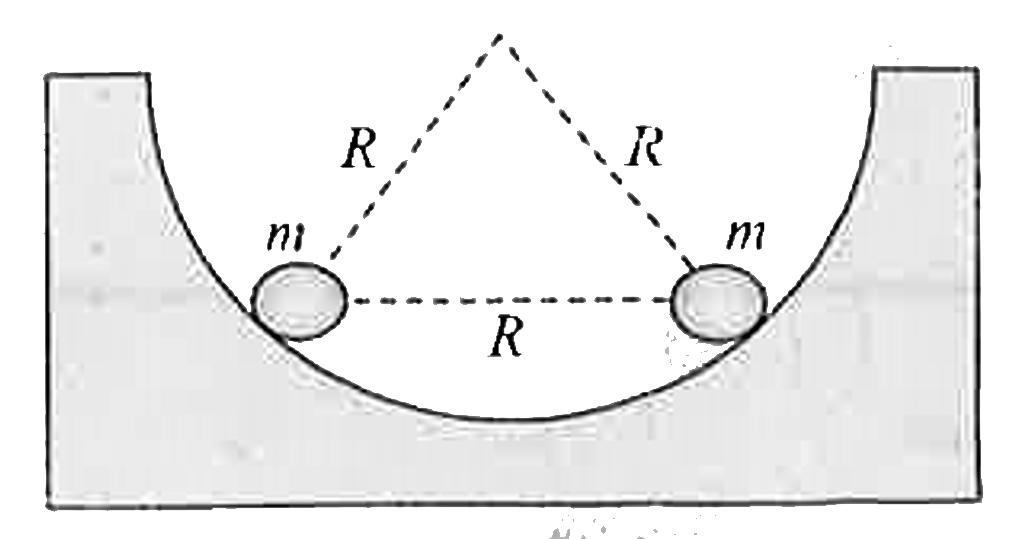 Aq=R(mgK√3)1/2Bq=(RmgK√3)1/2Cq=R(√3mgK)1/2Dq=(R√3mgK)1/2
Aq=R(mgK√3)1/2Bq=(RmgK√3)1/2Cq=R(√3mgK)1/2Dq=(R√3mgK)1/2Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3Two identical non-conducting spheres having charges of -12 nC and + 8 nC are touched together and then separated. The 3 nal charge on each is
A−2ncB−(23)ncC+2nCD+4nC
Two identical metallic sphere's having unequal opposite charges are placed at a distance 0.9 m apart in air. After bringing them in contact with each other they are again placed at the same distance apart. Now the force of repulsion between them is 0.025 N. calculate the final charges on each of them.
View SolutionTwo identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the ligth of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
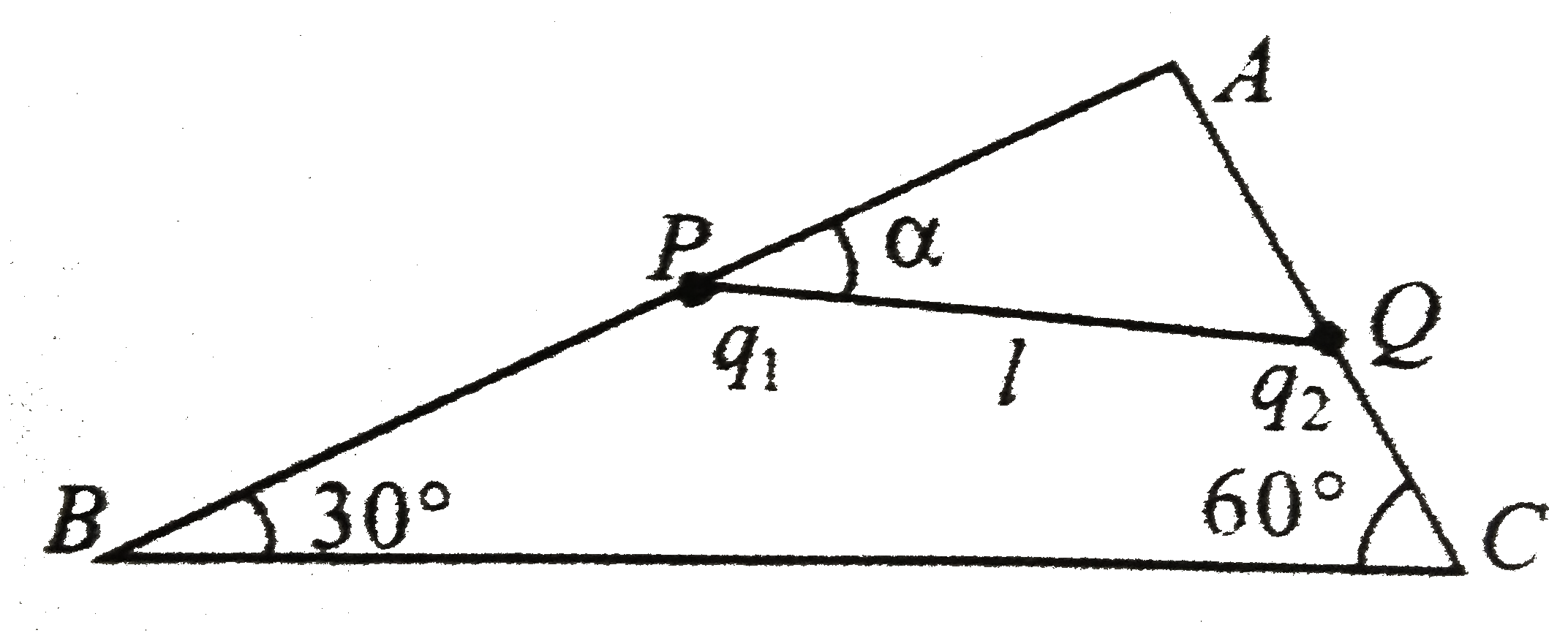
View SolutionA rigeid insulated wire frame in the form of a right-angled traingle ABC is set in a vertical plane as shown in fig. two beads of equal masses m each and carrying charges q1 and q2 are connected by a cord of length l and can slide without friction on the wires.
Cinsidering the case when the beads are stationary, determine
(i) the angel α
(ii) the tension in the cord, and
(iii) The normal recation on teh beads.
If the cord is now cut, what are the value of the charges for which the beads continue to remain stationary?
View SolutionTwo equal charges, +Q each, are at a distance r from each other. A third charge is placed on the line joining the above two charges such that all these charges are in equilibrium. Find q, in terms of Q.
View SolutionA large number (n) of identical beads, each of mass m and radius r are strung on a thin smooth rigid horizontal rod of length L(L>>r) an dare at rest at random positions. The rod is mounted between two rigid supports (see figure). If one of the beads is now given a speed v, the average force experienced by each support after a lone time is (assume all collision are elastic) :-
View Solution
