Using the concept of energy density, find the total energy stored in a
a. parallel plate capacitor
b. charged spherical conductor.
Video Solution
Text Solution
a. Electri field is uniform between the plates of the capacitor. The magnitude of this field is
E=σε0−qAε0 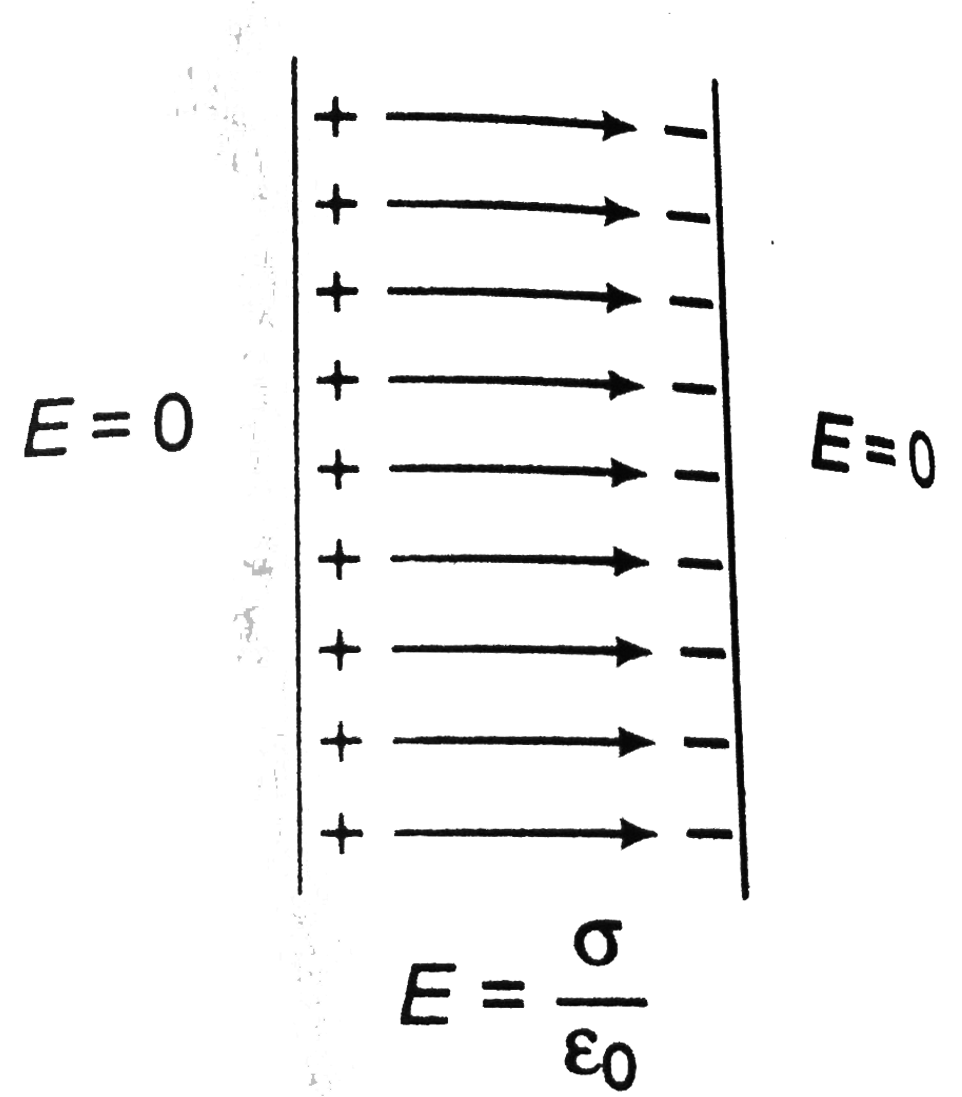
Therefore, the energy density u should also be constant.
u=12ε0E2=q22A2ε0
∴ Total stored energy,
U=(u)(totalvolume)
=q2(2A2ε0)(A.d)=q22(Aε0d)
=q22C
∴U=q22C
b. In case of a sphereical conductor (of radius r) the excess charge resides on the surface of the conductor. The field inside conductor is zero if extends from surface to infinity. And since the potential energy is stored in the field only, it will be stored in the region extgending from surface to infinity. But as the field is non uniform the energy density u is also no uniform. so, the total energy will be calculated by integration. Electric field at a distance r from the centre is
E=14πε0.qr2 
∴u(r)=12ε0E2
=12ε0{14πε0.qr2}2
energy stored i a volumn dV=(4πr2)dr is
dU=udV
∴ total energy strored, U=∫r=∞r=RdU
Substituting the values, we get 
U=q22(4πε0R)
or U=q22C
(as C=4πε0R)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - Exercise155videos
CAPACITORS
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
Find out total energy stored in the capacitors.
A500μJB300μJC600μJD1300μJ
Find the total energy stored in the capacitors in the given network.
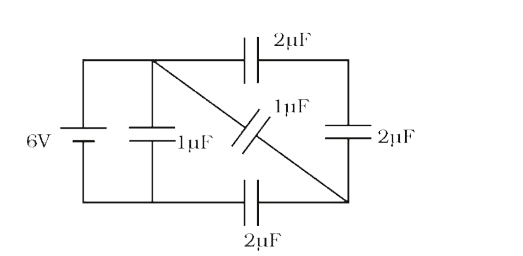 View Solution
View SolutionUsing the concept of energy density , show that the total energy stored by a shell of radius R and charge Q is Q28πε0R
View SolutionDerive an expression for energy density of a parallel plate capacitor.
View SolutionObtain the expression for the energy stored in a parallel plate capacitor of capacitance C charged to a potential V.
View SolutionFind the total energy stored in the capacitors in the given network of Fig.
View SolutionThe total electrostatic energy stored in both the capacitor is
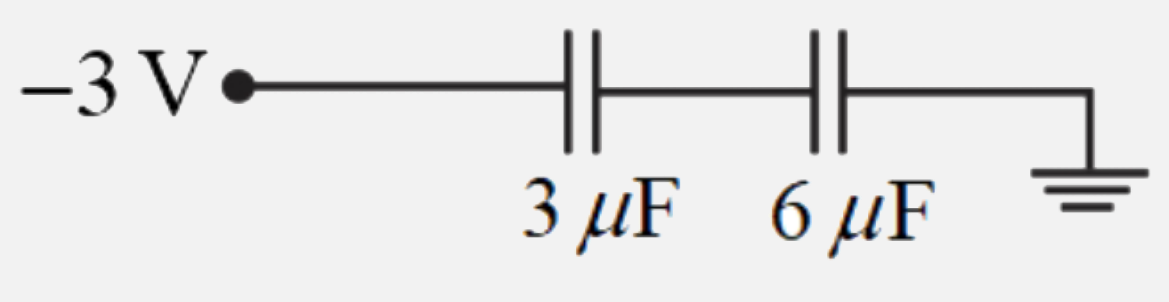 View Solution
View SolutionFind total energy stored in capacitors given in the circuit
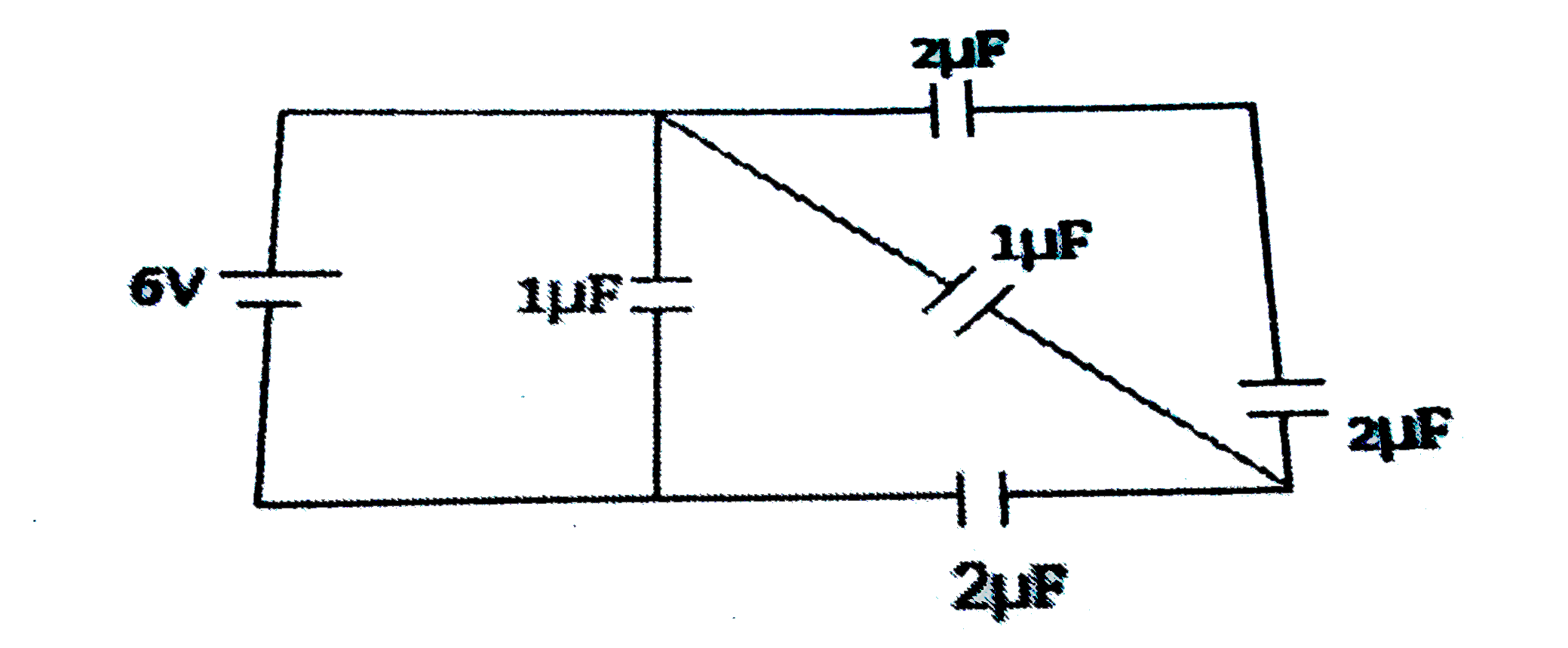 View Solution
View Solution

