A charged capacitor is discharged through a resistance. The time const

The value of time constant for the given circuit is

A $\frac{L}{R_{1} + r + R_{2}}$
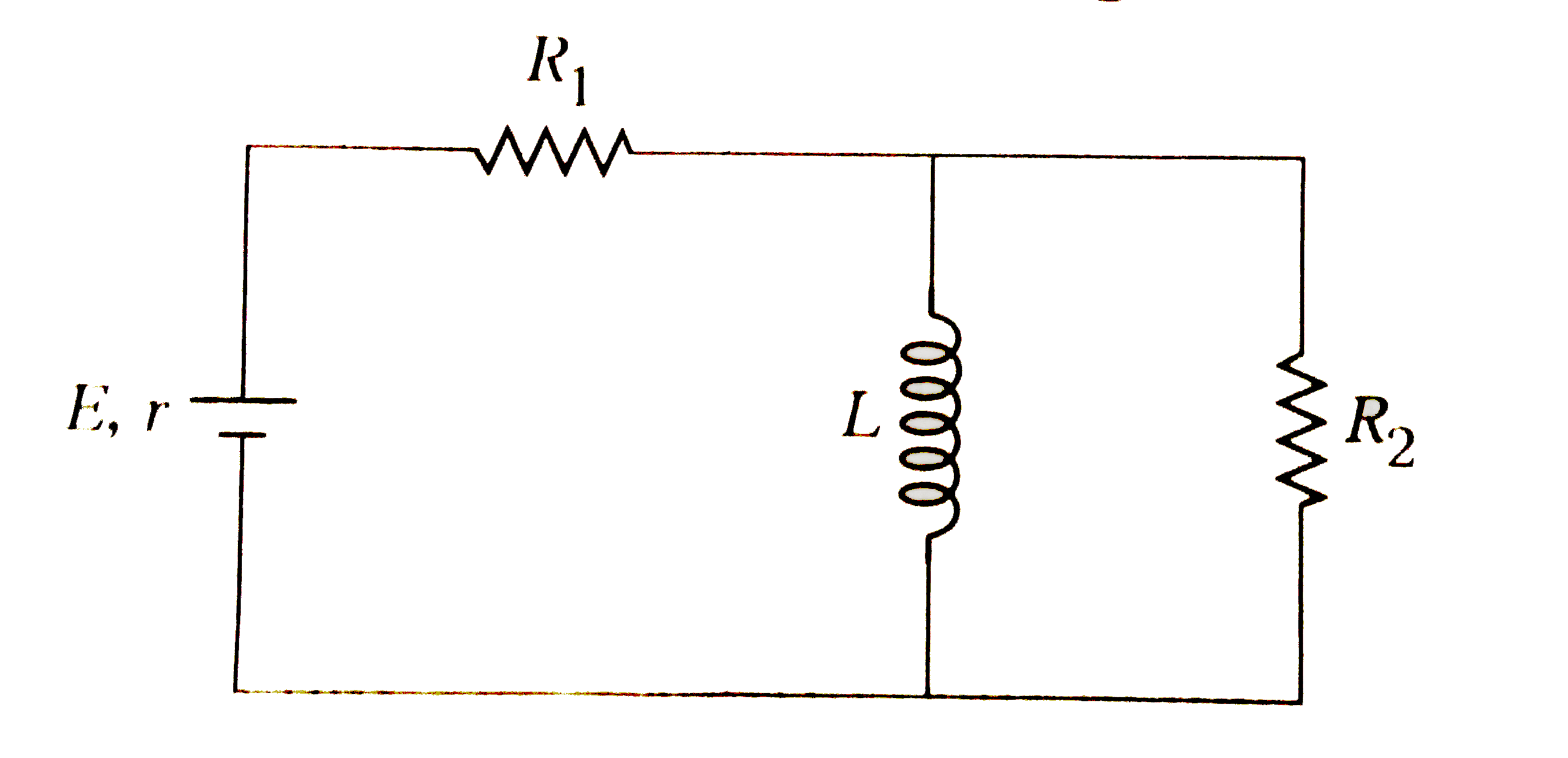B $\frac{L}{(R_{1} + r)}$
C $\frac{L (R_{1} + R_{2} + r)}{(R_{1} + r) R_{2}}$
DNone of these
A capacitor discharges through a resistance. The stored energy $U_{0}$ in one capacitive time constant falls to
A $U_{0} / e^{2}$
B $e U_{0}$
C $U_{0} / e$
Dnone of the above
The time constant of charging of the circuit shown in figure is

A $\frac{2}{3} R C$
B2RC
C3RC
D $\frac{3}{2} R C$

A charged capacitor is discharged through a resistance. The time constant of the circuit is $η$ . Then the value of time constant for the power dissipated through the resistance will be