Find the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
The correct Answer is:B, C
Let surface charge density is sigma
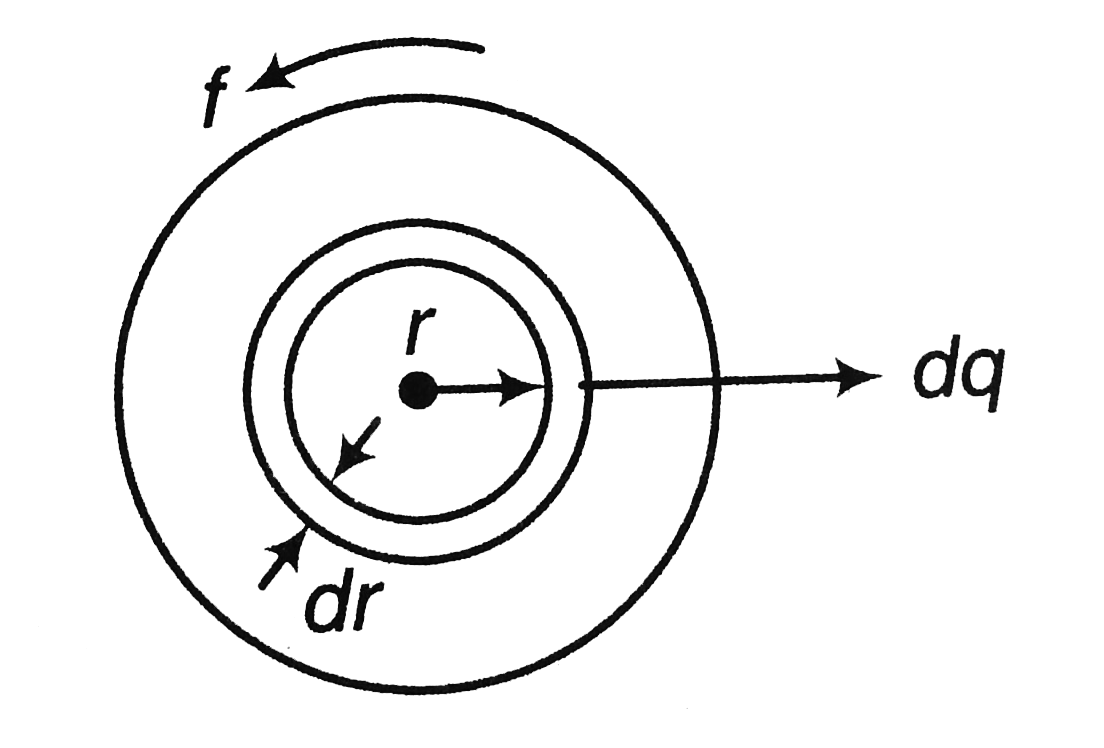
d=[(2πr)dr]σ
Equivalent current,
i=(dq)f
dM=iA=[(dq)f][πr2]
∴M=∫R0dM
dB=μ0i2r=μ0(dq)f2r
B=∫R0dB
now, we can find the ratio MB.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Find the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.
 View Solution
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View Solution
Knowledge Check
- Question 1 - Select One
Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
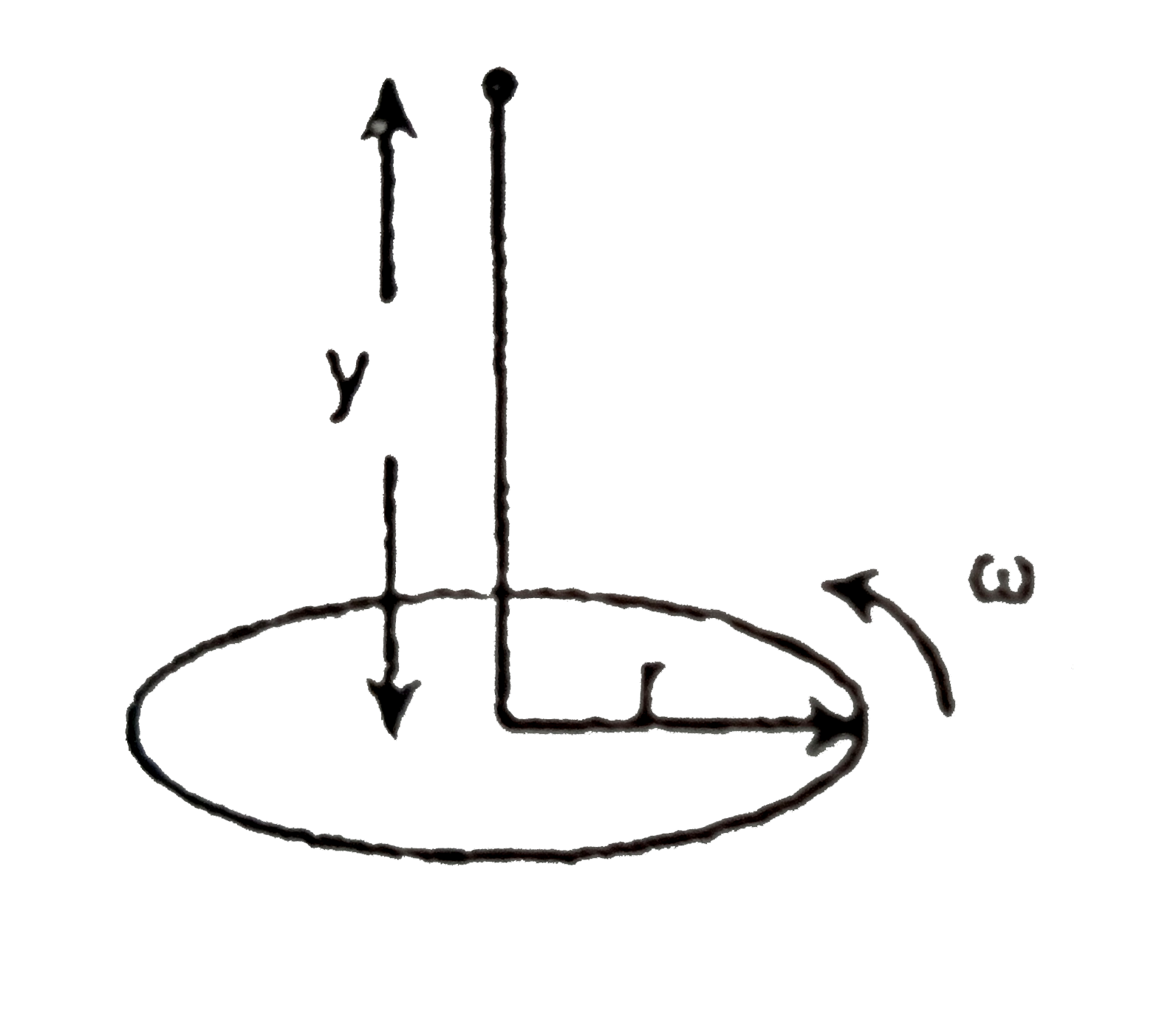 Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y) - Question 2 - Select One
A brass disc is rotating about its axis. If temperature of disc is increased then its
Aradius of gyration increases, but moment of inertia remains the sameBmoment of inertia increases but radius of gyration remains the sameCradius of gyration, moment of inertia both remain the sameDradius of gyration, moment of inertia both increase - Question 3 - Select One
A disc of the moment of inertia 'l1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1' . Another disc of moment of inertia 'I2'. having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is
A12[l1+l2l1l2]ω21B12[l1l2l1−l2]ω21C12[l1−l2l1l2]ω21D12[l2l2l1+l2]ω21
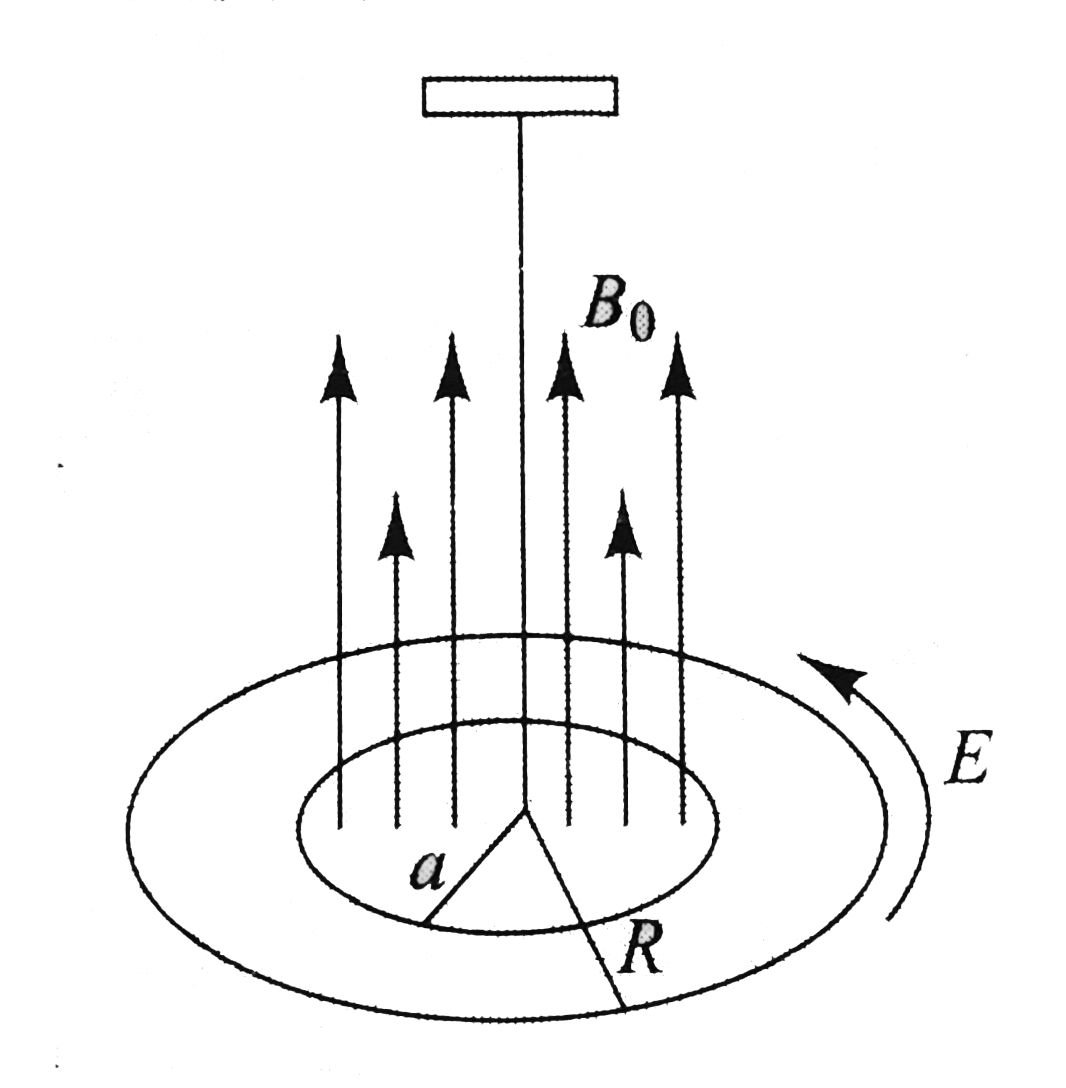
A line charge with linear charge density λ is wound around an insulating disc of mass M and radius R, which is then suspended horizontally as shown in Fig. 3.90, so that it is free to rotate. In the central region, of radius a, there is a uniform magnetic field B0, pointing up. Now the magnetic field is switched off, which causes the disc to rotate.
Find the angular speed with which the disc starts rotating.
 View Solution
View SolutionA charge Q is spread uniformly over an insulated ring of radius R.What is the magnetic moment of the ring if it is rotated with an angluar velocity ω about its axis?
View SolutionThe mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density σ. About its central axis of rotation it rotates at an angular speed ω. Find the magnetic moment of disc due to rotation of charges.
View SolutionA round disc of moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combination of discs is.
View Solution

