A rectangular loop PQRS made from a uniform wire has length a, width b and mass m. It is free to rotate about the arm PQ, which remains hinged along a horizontal line taken as the y-axis (see figure). Take the vertically upward direction as the z-axis. A uniform magnetic field →B=(3ˆi+4ˆk)B0 exists in the region. The loop is held in the x-y plane and a current I is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium

(a) What is the direction of the current I in PQ?
(b) Find the magnetic force on the arm RS.
(c) Find the expression for I in terms of B0, a, b and m
The correct Answer is:B
Let the direction of current in wire PQ is from P to Q and its magnitude be I.
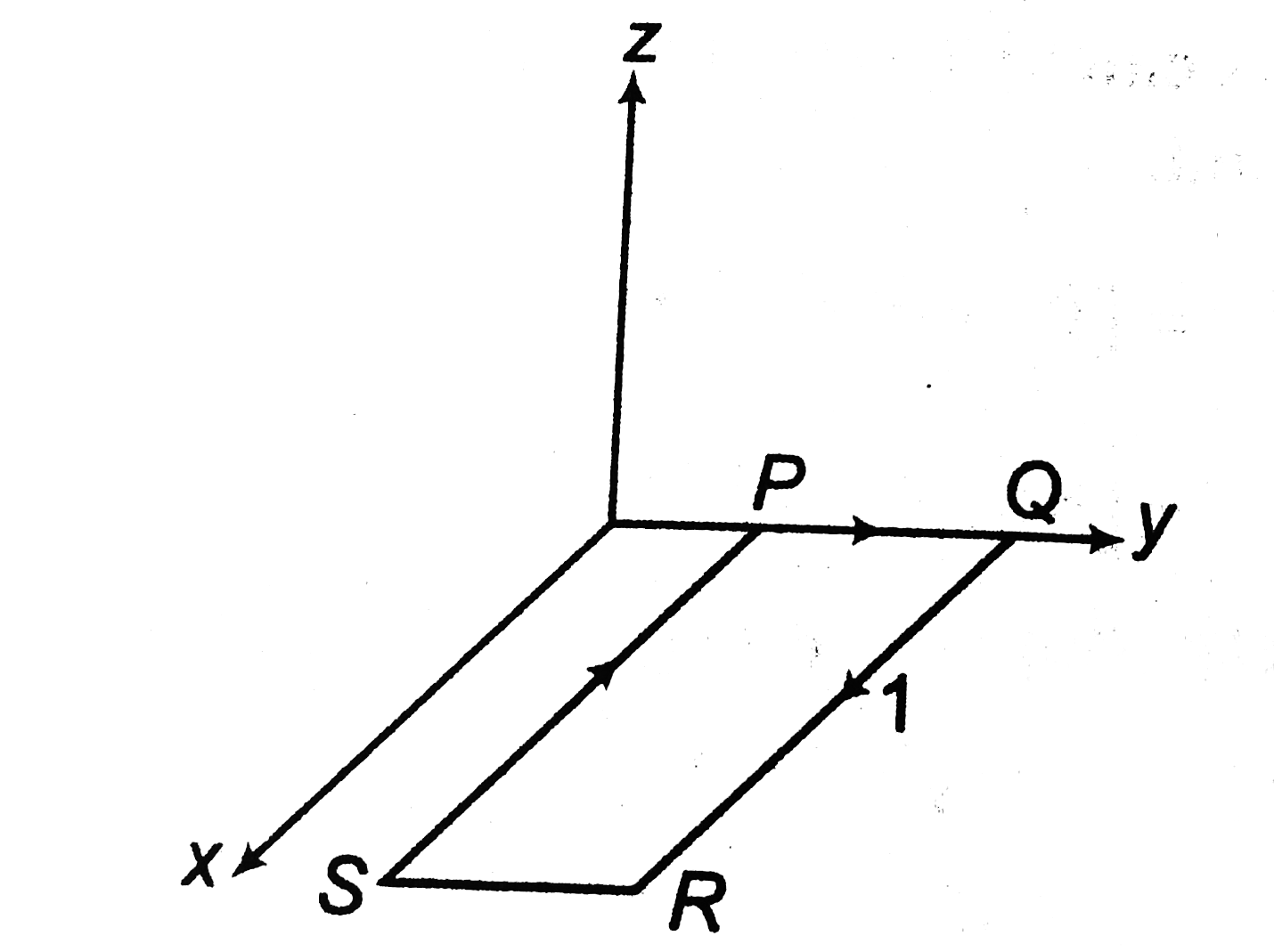
The magnetic moment of the given loop is
M=−Iabˆk
Torque on the loop due to magnetic force is
τ1=M×B
=(−Iabˆk)×(3ˆi+4ˆk)B0ˆi
=−3IabB0ˆj
Torque on weight of the loop about axis PQ is
τ2=r×F=(awˆi)×(−mgˆk)
=mga2ˆj
We see that when the current in the wire PQ is from P to Q,τ1 and τ2 are in opposite directions, so they can cancel each other and the loop may remain in equilibrium. so, the direction of current I in wire PQ is from P to Q. Further for equilibrium of the loop
|τ1|=|τ2|
or3IabB0=mga2
I=mg6bB0
Magnetic force on wire RS is
F=I((I×B)
=I[(_bˆj)×{(3ˆi+4ˆk)B0}]
F=IbB0(3ˆk−4ˆi)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
 View Solution
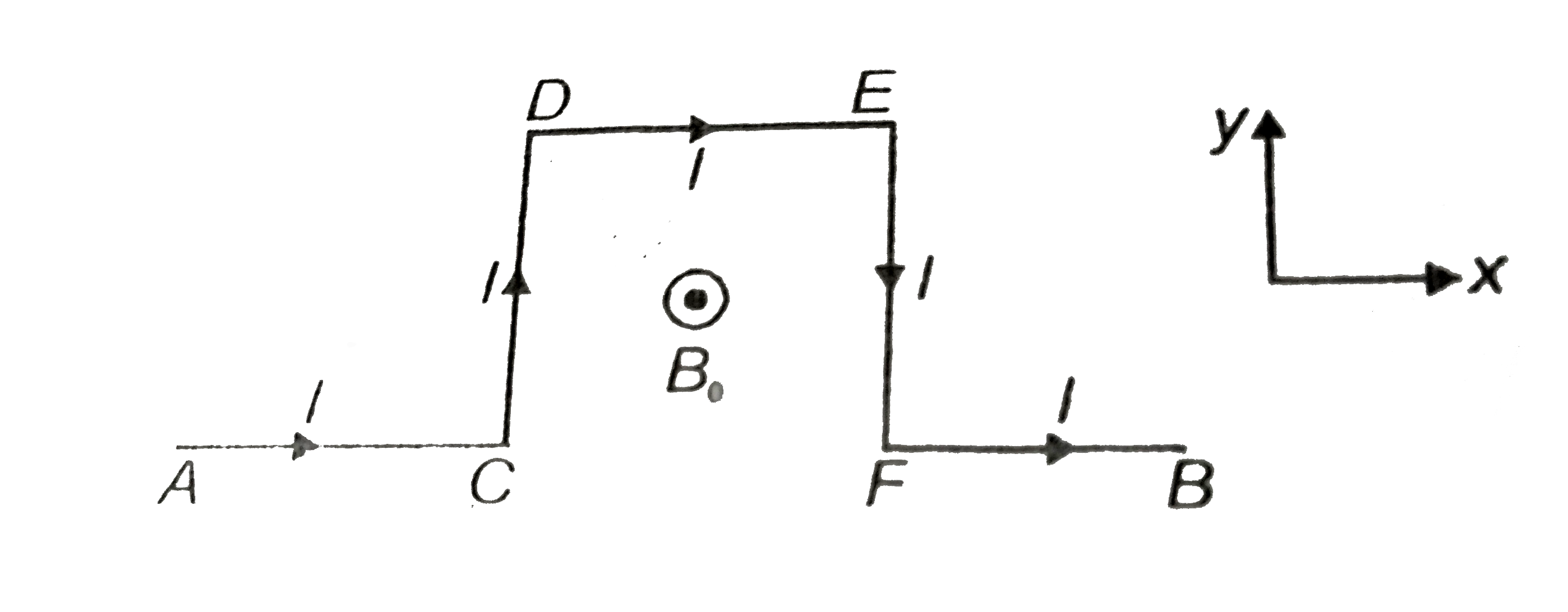
View SolutionA uniform magnetic field →B=B0ˆk exists in a region. A current carrying wire is placed in x-y plane as show. Find the force acting on the wire AB, if each section of the wire is of length 'a'.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
AzeroB2B0lv0CB0lv0D√2B0lv0 - Question 2 - Select One
A uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
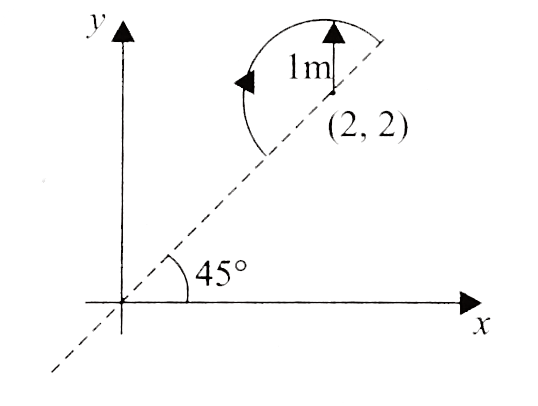 A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)
A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk) - Question 3 - Select One
In the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is
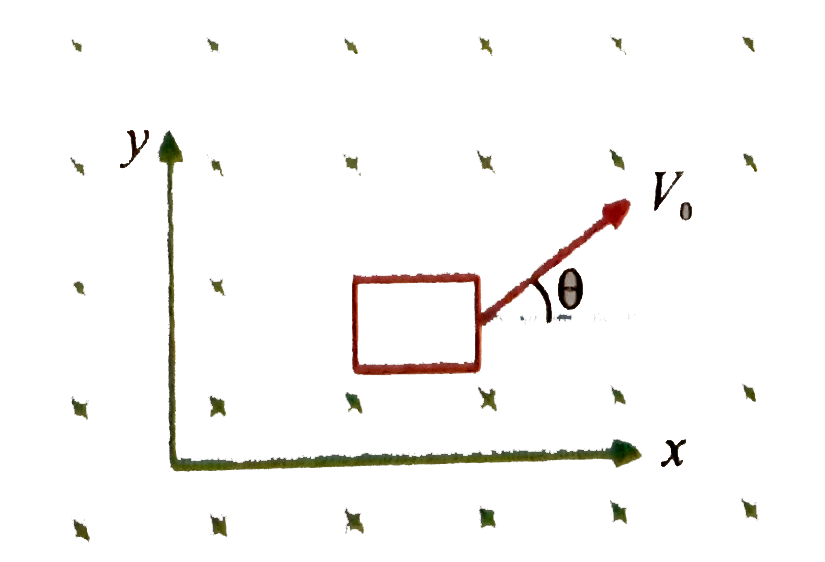 AzeroBAlong +x directionCalong −x directionDalong +y direction
AzeroBAlong +x directionCalong −x directionDalong +y direction
A thin conducting rod of length l=5m is moved such that its end B moves along the X-axis while end A moves along the Y-axis A uniform magnetic field B=6ˆk T exists
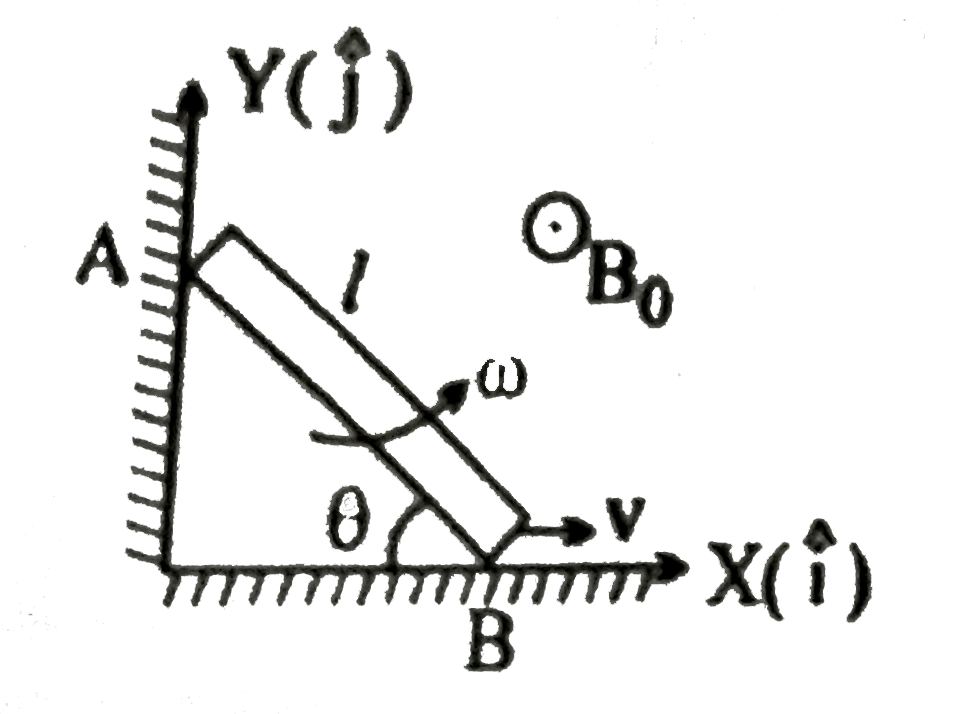 View Solution
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
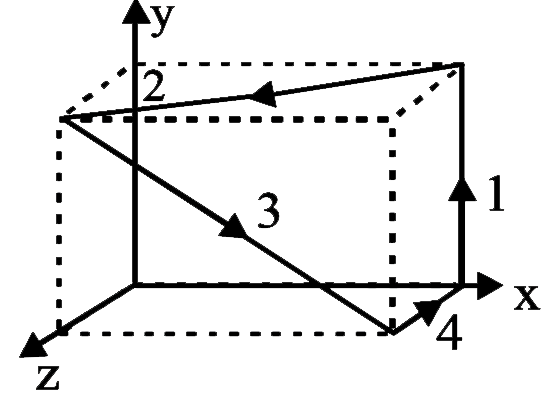
The net force on the loopView SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
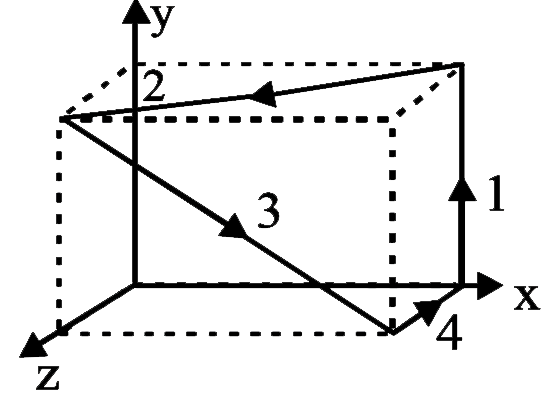
The net torque on the loopView SolutionA dipole of magnetic moment →m=30ˆjAm2 is placed along the y-axis in a uniform magnetic field →B=(2ˆi+5ˆj)T. The torque acting on it is
View SolutionA charge q moves with a velocity 2ms−1 along x-axis in a uniform magnetic field →B=(ˆi+2ˆj+3ˆk) then charge will experience a force
View Solution

