In the circuit diagram shown, initially there is no energy in the inductor and the capacitor, The switch is closed at t=0. Find the current I as a function of time if R=√L/C
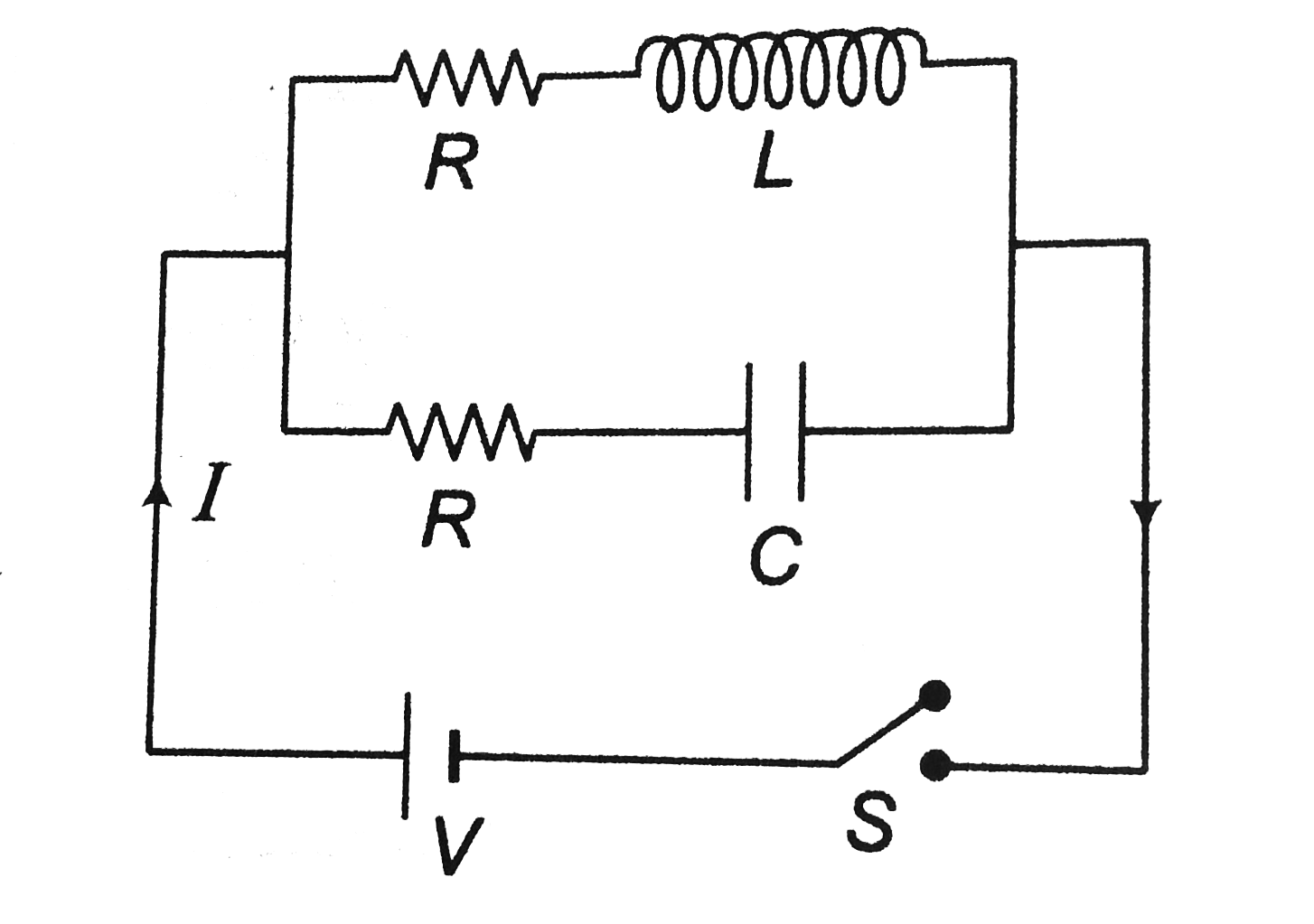
τL=LR
and τC=CR,τCτL=CR2L=CL.LC=1
∴τL=τC
∴ From the given condition τL=τC=τ(say)
Now, in L-R circuit
I1=VR(1−e−t/τ)
In CR circuit, I2=VRe−t/τ
∴I=I1+I2=VR=constant.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 2 Subjective
Explore 20 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Check point
Explore 60 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 2 Comprehension Based
Explore 13 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
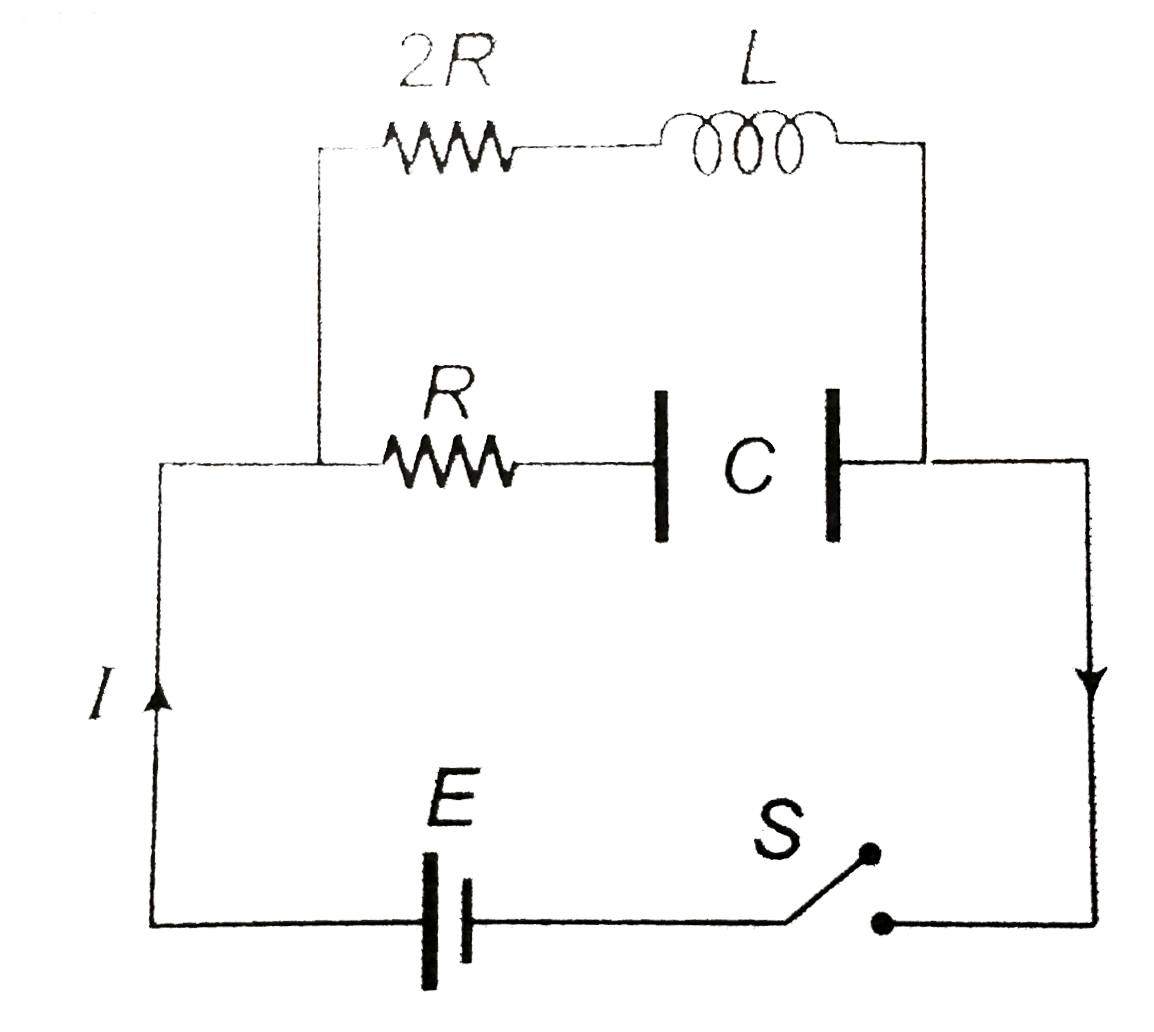
In the circuit diagram shown, intially there is no energy in the inductor and the capacitor. The switch is closed at t=0 . Find the current I as a function of time t .
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionA circuit contains an ideal cell and an inductor with a switch. Initially, the switch is open. It is closed at t=0. Find the current as a function of time.
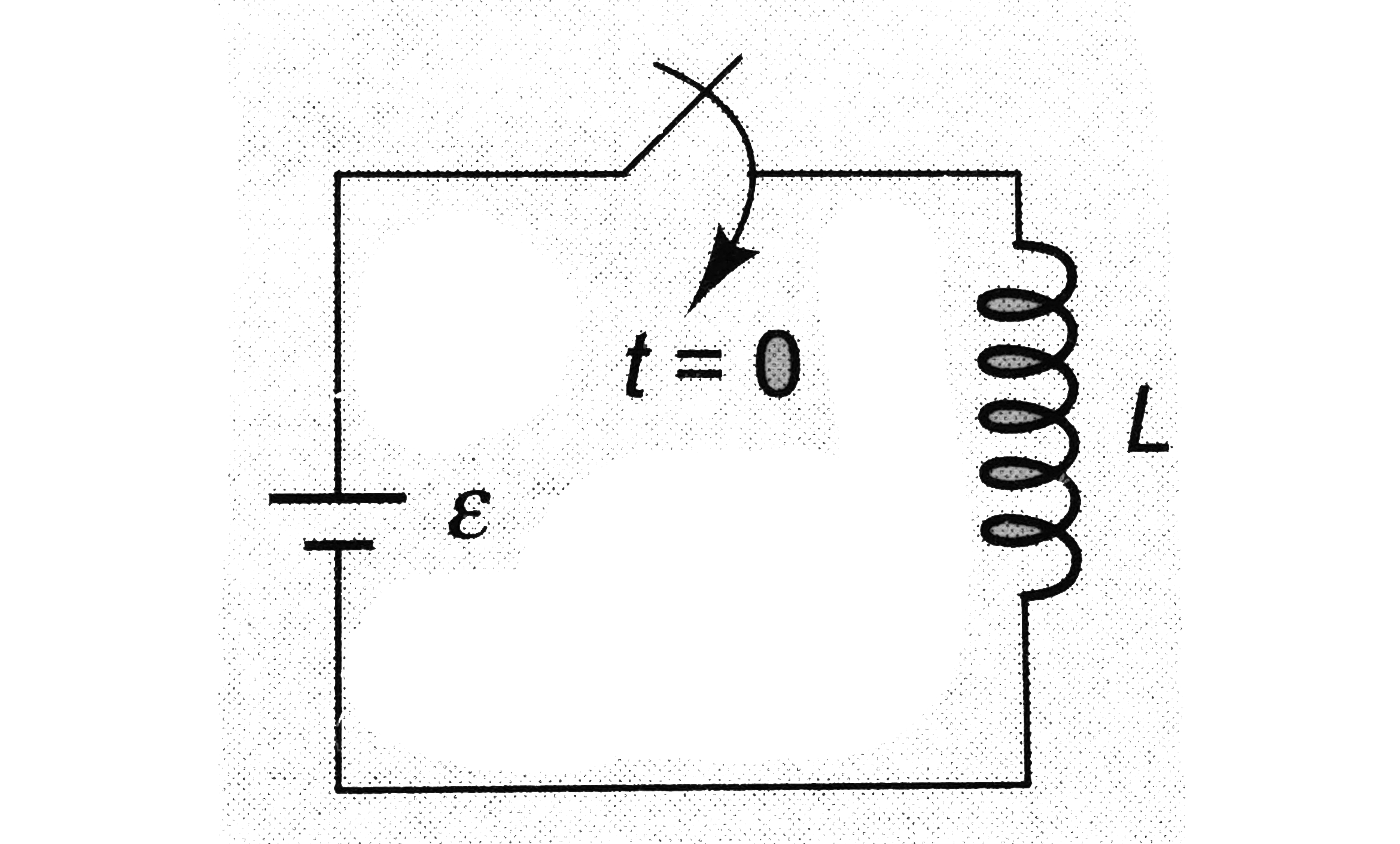
View SolutionA circuit contains an ideal cell and an inductor with a switch. Initially, the switch is open. It is closed at t=0. Find the current as a function of time.
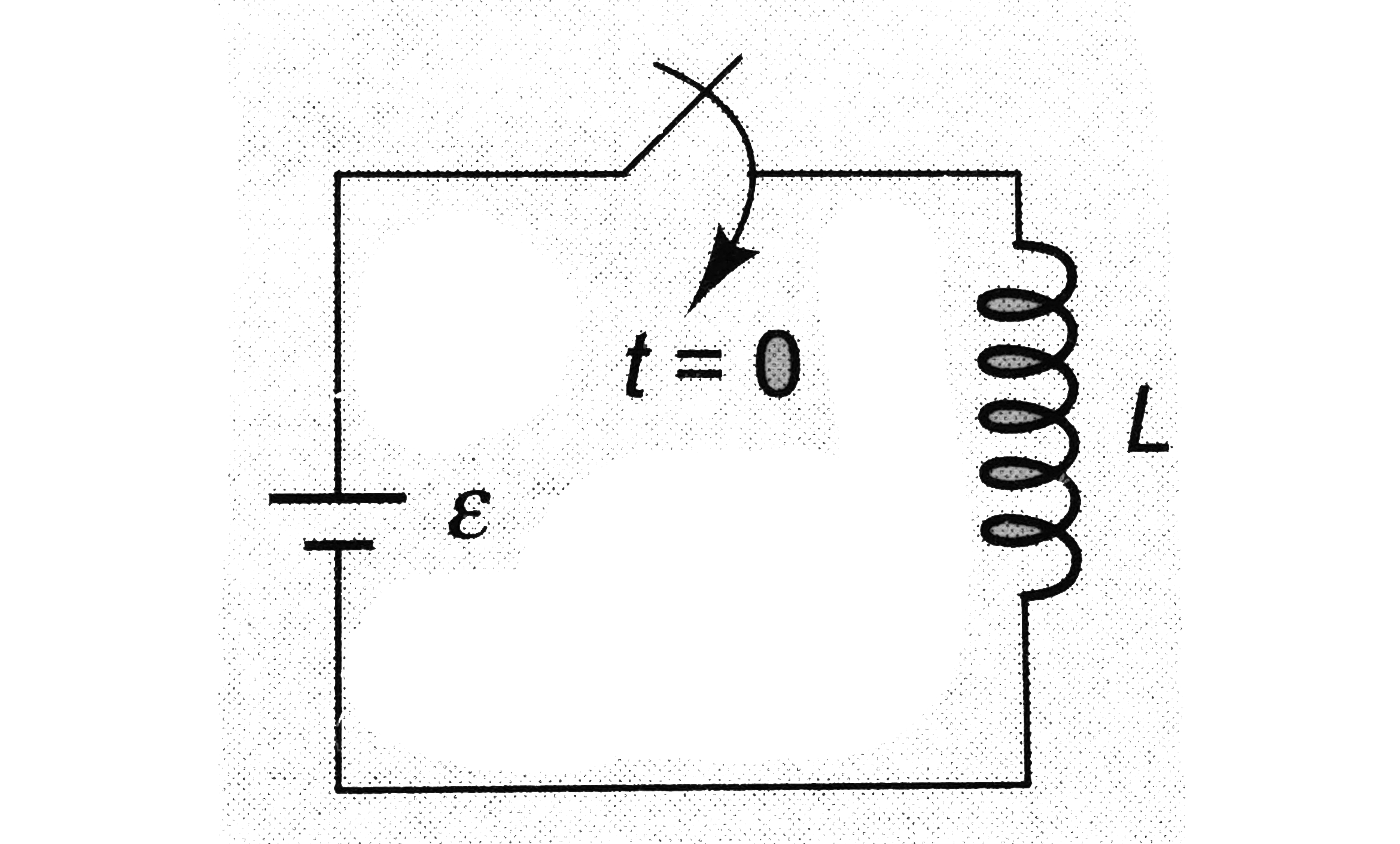
View SolutionA circuit contains an ideal cell and an inductor with a switch. Initially, the switch is open. It is closed at t=0. Find the current as a function of time.
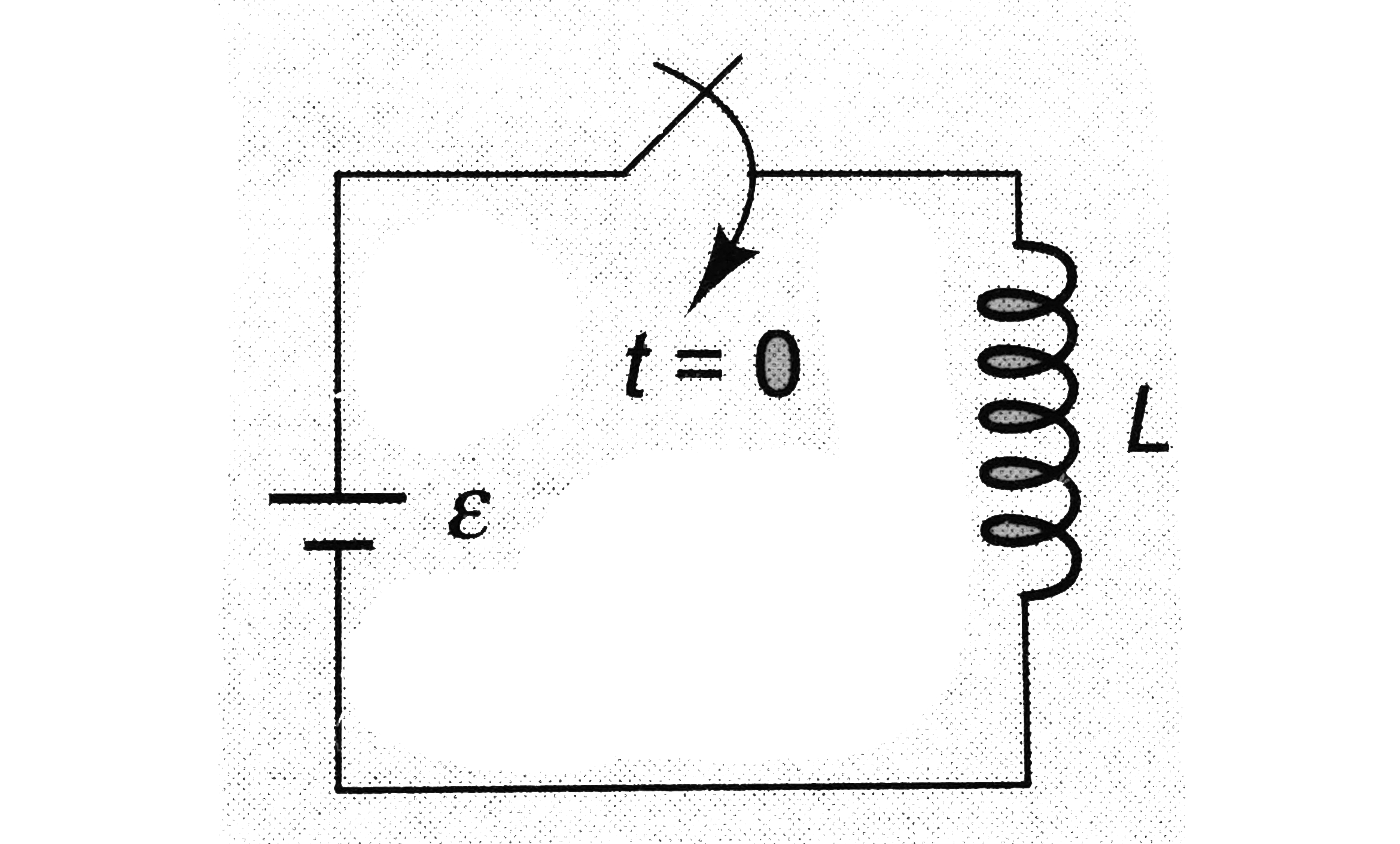
View SolutionConsider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View Solution
