A current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
To solve the problem step by step, we will first determine the inductance of the coil and then calculate the power developed in the circuit when a capacitor is connected in series with the coil.
Step 1: Calculate the Resistance (R) of the Coil
When the coil is connected to a DC source, the current is given as 4 A and the voltage is 12 V. The resistance can be calculated using Ohm's law:
R=VI=12V4A=3Ω
Step 2: Calculate the Inductive Reactance (XL) and Inductance (L)
When the coil is connected to an AC source with a voltage of 12 V and an angular frequency of 50 rad/s, the current flowing is 2.4 A. The root mean square (RMS) voltage is equal to the applied voltage (12 V).
Using the formula for the RMS current in an R-L circuit:
Irms=VrmsZ
Where Z is the impedance given by:
Z=√R2+(XL)2
Here, XL=ωL (inductive reactance). Rearranging the equation gives:
Z=VrmsIrms=12V2.4A=5Ω
Now, we can set up the equation:
5=√32+(ωL)2
Squaring both sides:
25=9+(ωL)2
Subtracting 9 from both sides:
16=(ωL)2
Taking the square root:
ωL=4
Now, substituting ω=50rad/s:
L=450=0.08H
Step 3: Calculate the Capacitive Reactance (XC)
The capacitance C is given as 2500 µF, which is 2500×10−6F. The capacitive reactance XC is given by:
XC=1ωC=150×2500×10−6=10.125=8Ω
Step 4: Calculate the Total Impedance (Z) in the Circuit
The total impedance Z when the capacitor is in series with the coil is given by:
Z=√R2+(XL−XC)2
Substituting the known values:
Z=√32+(4−8)2=√9+(−4)2=√9+16=√25=5Ω
Step 5: Calculate the Power Developed in the Circuit
The power P developed in the circuit can be calculated using the formula:
P=V2rmsZ⋅RZ
Substituting the known values:
P=1225⋅35=1445⋅35=43225=17.28W
Final Answers
- The inductance L of the coil is 0.08H.
- The power developed in the circuit is approximately 17.28W.
When the coil is connected to a DC source, the current is given as 4 A and the voltage is 12 V. The resistance can be calculated using Ohm's law:
When the coil is connected to an AC source with a voltage of 12 V and an angular frequency of 50 rad/s, the current flowing is 2.4 A. The root mean square (RMS) voltage is equal to the applied voltage (12 V).
The capacitance C is given as 2500 µF, which is 2500×10−6F. The capacitive reactance XC is given by:
The total impedance Z when the capacitor is in series with the coil is given by:
The power P developed in the circuit can be calculated using the formula:
- The inductance L of the coil is 0.08H.
- The power developed in the circuit is approximately 17.28W.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - Example Type 21videos
ALTERNATING CURRENT
- BOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - Example Type 31videos
ALTERNATING CURRENT
- BOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN63videos
ALTERNATING CURRENT
- BOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
When a 15 V dc source was applied across a choke coil then a current of 5 Amp flows in it. If the same coil is connected to a 15 V, 50 rad/s ac source a current of 3 Amp flows in the circuit. Determine the inductance of the coil. Also find the power developed in the circuit and its resonance frequency if a 2500 muf capacitor is connected in series with the coil
View SolutionA current of 6 A flows in a coil when connected to a dc source of 18 V. If the same coil is connected to an ac source of 20 V, 50 rad/s, a current of 4 A flows in the circuit. The inductance of the coil is 10x mH. Find out the value of x.
View Solution
Knowledge Check
- Question 1 - Select One
A current of 4 A flows in a coil when connected to a 12 V dc source. If the same coil is connected to a 12V,50rads−1 ac source, a current of 2.4 A flows of the coil in the circuit.
The inductance of the coil isA0.02HB0.04HC0.08HD1.0H - Question 2 - Select One
A current of 4 A flows in a coil when connected to a 12 V dc source. If the same coil is connected to a 12V,50rads−1 ac source, a current of 2.4 A flows of the coil in the circuit.
The power developed in the circuit of a 2500(μ)F capacitor that is connected in series with the coil isA17.28 WB8.64 WC10 WD15 W - Question 3 - Select One
A steady 4A flows in an inductor coil when connected to a 12V source as shown in figure. If the same coil is connected to an ac source of 12V, 50rad/s a currentd of 2.4A flows in the circuit as shown in figure2. Now after these observations , a capacitor fo capacitance 150F is connected in series with the coil and with same AC source as shown in figure 3.
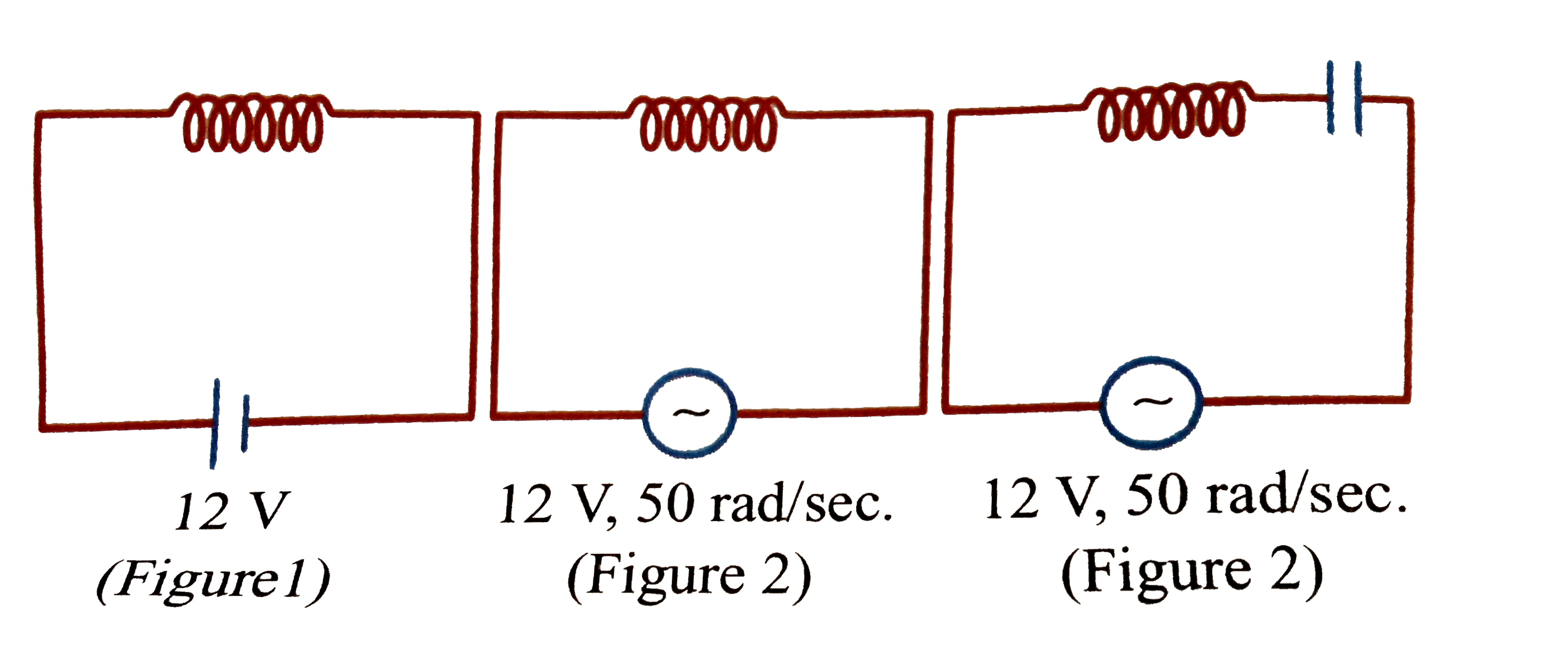
The resistance of the coil is:A1ΩB2ΩC3ΩD4Ω
A long solenoid connected to a 12V DC source passes a steady current of 2 A. When the solenoid is connected to an AC source of 12V at 50 Hz, the current flowing is 1A. Calculate inductance of the solenoid.
View SolutionAchoke coil is connected across 18 VDC supply and current of 6 A is found to flow through it in steady state. Now the same choke coil is connected to 15 VAC source whose angular frequency is 50 rad /s and current of 3 A is found to flow through it.
(i) Calculate self - inducatance of the coil.
(ii) If a capacitor of 2500 μF is connected in series with the coil then calculate power developed in the circuit.View SolutionA coil when connected across a 10 V d.c. supply draws a current of 2 A. When it is connected across 10 V - 50 hz a.c. supply the same coil draws a current of 1 A. Explain why? Hence determine self inductance of the coil.
View SolutionWhen a coil is connected to a 100 V D.C. supply, the current is 2 A. When the same coil is connected to A.C. source E=100√2sinωt, the current is 1 A. Find the inductive reactance used in the circuit.
View SolutionWhen a coil is connected to a D.C. source of e.m.f. 12 volt, then a current of 4 ampere flows in it. If the same coil is connected to a 12 volt, 50 cycle/s A.C. source, then the current flowing in it is 2.4A. The self inductance of the coil will be
View Solution

