Surfaces of a thin equi-convex glass lens have radius of curvature R. Paraxial rays are incident on it . If the final image is formed after n internal reflections, calculate distance of this image from pole of the lens. Refractive index of glass is μ.
The rays will first get refracted, then n-times reflected and finally again refracted.
So, using μ2v−μ1u=μ2−μ1R for first refraction, we have

μvi−1∞=μ−1R⇒vi=(μμ−1)R
For first reflection, let us use 1v+1u=1f=2R
∴1v1+(μ−1μR)=−2Ror1v1=−(3μ−1μR)
For second reflection, 1v2+(3μ−1μR)=−2R or 1v2=−(5μ−1μR)
Similarly, after nth reflection, 1vn=−[(2n+1)μ−1μR]
Finally, using μ2v−μ1u=μ2−μ1R, we have
1vf=−{(2n+1)μ−1R}=1−μ−R
vf=R2(μn+μ−1)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.13videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.22videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 113videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
CHC The radius of curvature of each surface of an equiconvex lens is R = 42 cm. Refractive index of the glass = 1.25. If the final image forms after four internal reflections (but not TIR) inside the lens (for paraxial ray incident beam parallel to principal axis) calculate the distance of the image from the lens, in cm.
View SolutionA parallel beam of light passes parallel to the principal axis and falls on one face of a thin convex lens offocal length f and after two internal reflections from the second face forms a real image. The distance of image from lens if the reflactive index of material of lens is 1.5 :
View Solution
Knowledge Check
- Question 1 - Select One
If the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
Af=R2(μ+1)Bf=2R(μ+1)Cf=2Rμ+1Df=R2(μ−1) - Question 2 - Select One
A thin equi-convex lens having radius of curvature 10 cm is placed as shown in figure. Calculate focal length of the lens, if parallel rays are incident as shown.
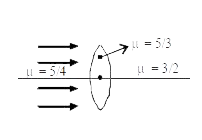 A1207 cmB1607 cmC1807 cmDNone
A1207 cmB1607 cmC1807 cmDNone - Question 3 - Select One
An equi-convex glass lens with radius of each face as R is placed in air (.aug=3/2). "If there is water in the object space and air in the image space and given" .auw=4/3, the focal length of the lens is
A4 RB2 RC3R2DR
An observer holds in front of himself a thin equi convex lens. R is the radius of curvature of each face. He sees two images of his nose, one erect and the other inverted. Explain the formation of these images and assuming the refractive index of glass to be 1.50 prove that he will see two erect images if the distance of the lens is less than 0.25 R from his nose.
View SolutionA light ray from air is incident on a glass plate of thickness t and refractive index μat an angle of incidence equal to the angle of total internal reflection of glass. Compute the displacement of the ray due to this plate in terms of thickness and refractive index of glass μ.
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ1.5.
View SolutionAn equiconvex lens of refractive index 1.5 has its two surfaces having radius of curvature of 30 cm. A point object has been placed on the principal axis at a distance of 60 cm from the lens. Find the distance of image from the lens formed by the rays which suffer refraction at first surface, reflection at second surface, again a reflection on the first surface and finally a refraction from the second surface.
View SolutionThere is a thin double convex lens having surfaces of radius of curvature R and 2R. Lens is kept in air and refractive index of the material of the lens is μ. Focal length of the lens
View Solution

