The given equi-convex lens is broken into four parts and rearranged as shown. If the initial focal length is f, then after rearrangement the equivalent focal length is

A

$f$

B

$f / 2$

C

$f / 4$

D

$4 f$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Focal length of any one part will be $2 f .$
$∴ \frac{1}{F} = \frac{1}{2 f} + \frac{1}{2 f} + \frac{1}{2 f} + \frac{1}{2 f} or F = \frac{f}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1videos
REFRACTION OF LIGHT
BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective
29videos
REFRACTION OF LIGHT
BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
13videos
REFRACTION OF LIGHT
BOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9videos
REFLECTION OF LIGHT
BOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12videos
SEMICONDUCTORS

Similar Questions

Knowledge Check

Question 1 - Select One
The given equi-convex lens is broken into four parts and rearranged as shown. If the initial focal length is f, then after rearrangement the equivalent focal length is

A $f$
B $f / 2$
C $f / 4$
D $4 f$
Question 2 - Select One
The given lens is broken into four parts rearranged as shown. If the initial focal length is f, then after rearrangement the equivalent focal length is

Af
B $f / 2$
C $f / 4$
D $4 f$
Question 3 - Select One

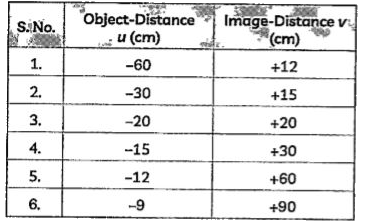
The focal length of the convex lens is
A $+ 10$ cm
B $+ 20 c m$
C $- 10 c m$
D $- 20 c m$

DC PANDEY-REFRACTION OF LIGHT-Level 1 Objective

Home
Ask Doubt
Profile