A bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
h2h1
h1h2
h1+h2h1−h2
h1−h2h1+h2
The correct Answer is:A
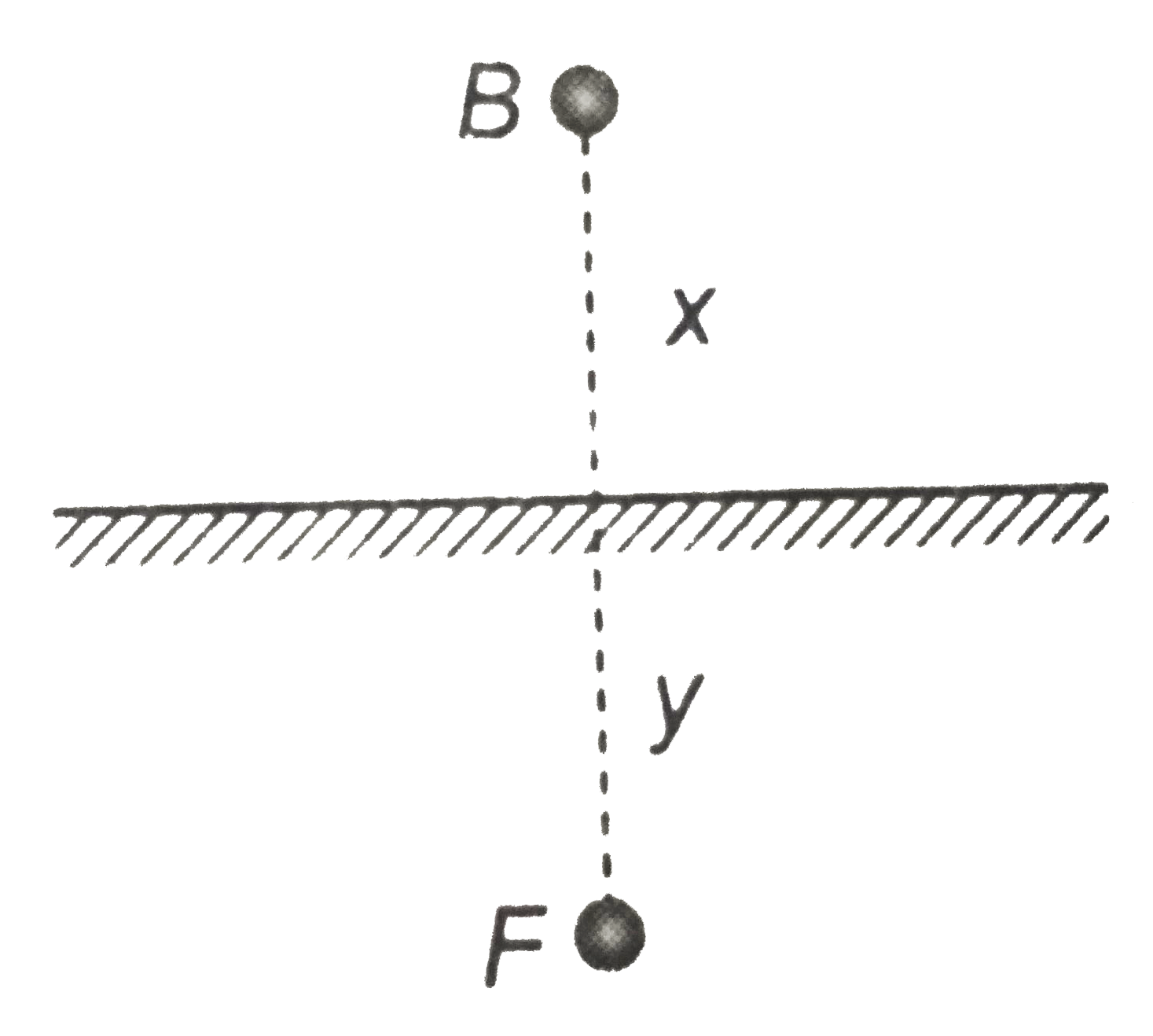
h1=x+yμ…(i)
h2=y+μx……..(ii)
Eq.(i) can be written as
μx+yμ=h1orh2μ=h1orμ=h2h1
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Find out the following in the figure shown below :
(a) The apparent speed of the fish as observed by the bird
(b) The apparent speed of the bird as observed by the fish
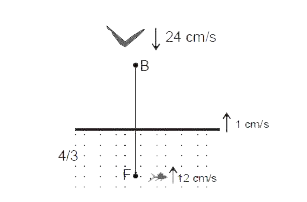
View SolutionFind out the following in the figure shown below :

(a) The apparent distance of the fish from the surface as observed by the bird
(b) The apparent distance of the bird from the surface as observed by the fish
View Solution
Knowledge Check
A bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
Ah2h1Bh1h2Ch1+h2h1−h2Dh1−h2h1+h2A bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2A fish in water (refractive index n ) looks at a bird vertically above in the air. If y is the height of the bird and x is the depth of the fish from the surface, then the distance of the bird as estimated by the fish is
Ax+y(1+1n)By+x(1−1n)Cy+x(1−1n)Dx+y(1−1n)
Consider the situation as shown in the diagram.
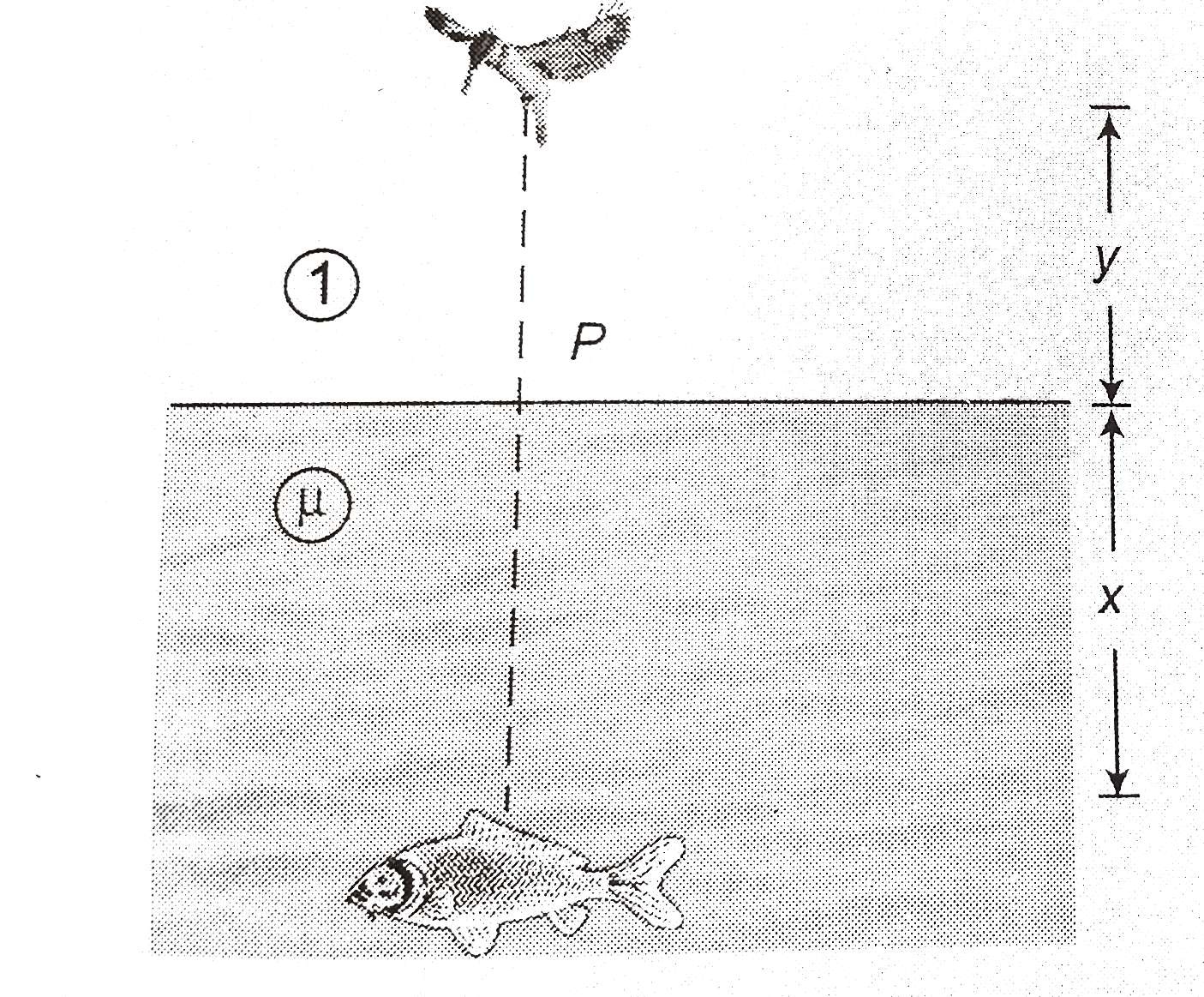
Find the distance between bird and fish as seen by (a) bird and (b) fish
View SolutionThe back wall of an aqaurium is a mirror that is 30 cm away from the fron wall. The sides to the tank are negligibly thin. A fish is swimming midway between the front and back walls.
a. An image of the fish appears behind the mirror. How far dows this image appear to be from the front wall of the aquarium?
b. Would the refractive index of the liquid have to be larger or smaller in order for the image of the fish to appear in front of the mirror, rather than behind it? Find the limiting value of this refractive index. Initially, water is there in aquarium having refractive index 4/3
View SolutionA fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
View SolutionA bird in air is at a height ‘y’ from the surface of water. A fish is at a depth ‘x’ below the surface of water. The apparent distance of fish from the bird is (The refractive index of water is n )
View SolutionA bird flying in sky and a fish in water look at each other. For which of them, the distance between them seem to be less?
View Solution
