A sphere (μ=43) of radius 1m has a small cavity of diameter 1cm at its centre. An observer who is looking at it from tight, sees the magnification of diameter of the cavity as
43
34
1
0.5
The correct Answer is:A
Cavity of placed at centre. Hence, image of cavity
is also formed at centre, as all rays fall normal to
surface at all point. (so pass undedicated).

Now, m=(μ1μ2)(vu)
=(4/3)1(1m1m)
=43
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option3videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions8videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
A glass sphere of radius 5 cm has a small bubble at a distance 2 cm from its centre. The bubble is viewed along a Diameter of the sphere from the side on which it lies.How far from the surface will it appear.Refractive index of glass is 1.5
2.5 cm behind the surfaceView SolutionA glass sphere of radius 15 cm has a small bubble 6 cm from its centre. The bubble is viewed along a diameter of the sphere from the side on which it lies. How for from the surface will it appear to be if the refractive index of glass is 1.5 ?
View Solution
Knowledge Check
- Question 1 - Select One
A metallic sphere of diameter D has a cavity of diameter d at its centre. If the sphere is heated, the diameter of the cavity will:
ADecreaseBIncreaseCRemain unchangedDDecrease if d<D/2 and increase if d>D/2 - Question 2 - Select One
A glass sphere (μ =1.5) of radius 20 cm has small air bubble 4 cm below its centre. The sphere is viewed from outside and along vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
A13.33B26.67C15D30 - Question 3 - Select One
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
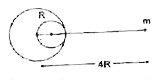 View Solution
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric field (magnitude only) at the center of the cavity will be :View Solution

