A ray of light is refracted through a sphere whose material has a refractive index μ in such a way that it passes through the extremities of two radii which make an angle β with each other. Prove that if α is the deviation of the ray caused by its passage through the sphere, then
cos(β−α2)=μcos(βα)
The correct Answer is:A
δTotal=δP+δQ

∴α=(i−r)+(i−r)
ori−r=α2….(i)
Further, in ∠OPQ,r+r+β=180∘
∴r=90∘−β2…..(ii)
From Eq.(i),
i=r+α2=90∘+(α−β2).....(iii)
μ=sinisinr=sin[90∘+(α−β2)]sin(90−β2)
=cos(β−α2)cos(βα)
or cos(β−α2)=μcosβ2 Henced proved
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
41 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective
29 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A ray of light passes through a transparent sphere of refractive index μ and radius R. If b is the distance between the incident ray and diameter of the sphere which is parallel to that ray, What is the value of the deviation?
View SolutionA ray of light falls on the surface of a spherical glass paper weight making an angle α with the normal and is refracted in the medium at an angle β. The angle of deviation of the emergent ray from the direction of the incident ray is :
View Solution
Knowledge Check
A ray of light passes through a glass plate of thickness and refractive indexμ if the speed of light in vacuum is c,then the time taken by light in passing through the plate will be-
AμtBμtcCtccDtμcA ray of light falls on the surface of a spherical glass paper weight making an angle α with the normal and is refracted in the medium at an angle β. The angle of deviation of the emergent ray from the direction of the incident ray is :
A(α−β)B2(α−β)C(α−β)/2D(β−α)
A ray of light falls on the surface of a spherical glass paper weight making an angle α with the normal and is refracted in the medium at an angle β. The angle of deviation of the emergent ray from the direction of the incident ray is :
View SolutionFind the equation of the straight lines passing through the following pair of point: (a cosα, asinα)and (a cosβ, asinβ)
View SolutionPath of ray of light passing through three liquids of refractive indices μ1,μ2,μ3 is as shown in Fig. Which liquid has the smallest index of refraction ?
 .
.
View SolutionIf αandβ are two points on the hyperbola x2a2−y2b2=1 and the chord joining these two points passes through the focus (ae, 0) then ecosα−β2=
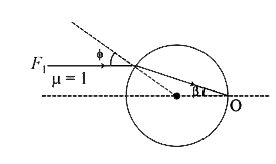
View SolutionA ray of light enters a spherical drop of refractive index (μ=54) as shown in the figure. The value of 100 cos β is (where ϕ is the angle for which the ray after refraction passes through the point ) O as shown in the figure.
View SolutionA ray of light suffers a deviation of 3.2∘ on passing through a thin prism of angle 5∘. What is the refractive index of the material of the prism ?
View Solution
