Maximum kinetic energy of a photoelectron is E when the wavelength of incident light is . If energy becomes four times when wavelength is reduced to one thrid, then work function of the metal is
The correct Answer is:B
To solve the problem step by step, we will use the concepts of photoelectric effect and the equations associated with it.
Step 1: Write down the equation for maximum kinetic energy of a photoelectron.
The maximum kinetic energy (K.E.) of a photoelectron can be expressed as:
K.E.=hcλ−ϕ
where:
- K.E. is the maximum kinetic energy,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light,
- ϕ is the work function of the metal.
Step 2: Set up the first condition using the given information.
From the problem, we know that when the wavelength is λ, the maximum kinetic energy is E. Therefore, we can write:
E=hcλ−ϕ
This is our Equation 1.
Step 3: Set up the second condition with the new wavelength.
Now, when the wavelength is reduced to λ3, the maximum kinetic energy becomes four times the previous value, which is 4E. We can express this as:
4E=hcλ3−ϕ
This simplifies to:
4E=3hcλ−ϕ
This is our Equation 2.
Step 4: Substitute E from Equation 1 into Equation 2.
From Equation 1, we can express E as:
E=hcλ−ϕ
Now, substituting this into Equation 2 gives:
4(hcλ−ϕ)=3hcλ−ϕ
Step 5: Expand and simplify the equation.
Expanding the left side:
4hcλ−4ϕ=3hcλ−ϕ
Now, rearranging the equation:
4hcλ−3hcλ=4ϕ−ϕ
This simplifies to:
hcλ=3ϕ
Step 6: Solve for the work function ϕ.
Now, we can express the work function ϕ:
ϕ=hc3λ
Conclusion
Thus, the work function of the metal is:
ϕ=hc3λ
The maximum kinetic energy (K.E.) of a photoelectron can be expressed as:
K.E.=hcλ−ϕ
where:
- K.E. is the maximum kinetic energy,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light,
- ϕ is the work function of the metal.
From the problem, we know that when the wavelength is λ, the maximum kinetic energy is E. Therefore, we can write:
E=hcλ−ϕ
This is our Equation 1.
Now, when the wavelength is reduced to λ3, the maximum kinetic energy becomes four times the previous value, which is 4E. We can express this as:
4E=hcλ3−ϕ
This simplifies to:
4E=3hcλ−ϕ
This is our Equation 2.
From Equation 1, we can express E as:
E=hcλ−ϕ
Now, substituting this into Equation 2 gives:
4(hcλ−ϕ)=3hcλ−ϕ
Expanding the left side:
4hcλ−4ϕ=3hcλ−ϕ
4hcλ−3hcλ=4ϕ−ϕ
This simplifies to:
hcλ=3ϕ
Now, we can express the work function ϕ:
ϕ=hc3λ
Thus, the work function of the metal is:
ϕ=hc3λ
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 1 Subjective
40 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Single Correct
22 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Level -1 Assertion And Reason
10 Videos
- MODERN PHYSICSBOOK - DC PANDEYCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
Maximum kinetic energy of photoelectrons from a metal
surface is K0 when wavelngth of incident light is λ. If wavelength is decreased
to λ∣2, the maximum kinetic energy of photoelectrons becomes
(a) =2K0 (b)>2K0 (c ) <2K0
View SolutionThe maximum kinetic energy of photoelectron is doubled when the wavelength of light incident on the photosensitive changes from λ1 to λ2. Deduce expression for the threshold wavelength and work function for metals in terms of λ1 and λ2
View Solution
Knowledge Check
The graph between the energy of photoelectrons E and the wavelength of incident light (λ) is
A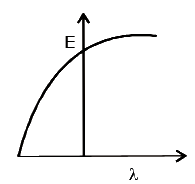 B
B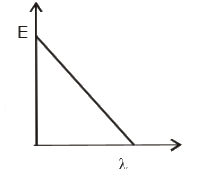 C
C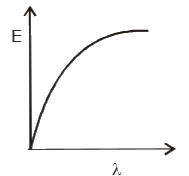 D
D
The KE of the photoelectrons is E when the incident wavelength is λ2. The KE becomes 2E when the incident wavelength is λ3. The work function of the metal is
AhcλB2hcλC3hcλDhc3λIf light of wavelength λ1 is allowed to fall on a metal , then kinetic energy of photoelectrons emitted is E1. If wavelength of light changes to λ2 then kinetic energy of electrons changes to E2. Then work function of the metal is
AE1E2(λ1−λ2)λ1λ2BE1λ1−E2λ2(λ1−λ2)CE1λ1−E2λ2(λ2−λ1)Dλ1λ2E1E2(λ2−λ1)
The maximum kinetic energy of the photoelectrons emitted is doubled when the wavelength of light incident on the photosensitive surface changes from λ1 to λ2. Deduce expressions for the threshold wavelength and work function for the metal surface in terms of λ1andλ2.
View SolutionThe kinetic energy of an electron is E when the incident wavelength is λ To increase ti KE of the electron to 2E, the incident wavelength must be
View SolutionMaximum kinetic energy of photoelectrons emitted from a metal surface, when light of wavelength λ is incident on it, is 1 eV. When a light of wavelength λ3 is incident on the surfaces, maximum kinetic energy becomes 4 times. The work function of the metal is
View SolutionThe kinetic energy of the most energetic photoelectrons emitted from a metal surface is doubled when the wavelength of the incident radiation is reduced from λ1 to λ2 The work function of the metal is
View Solution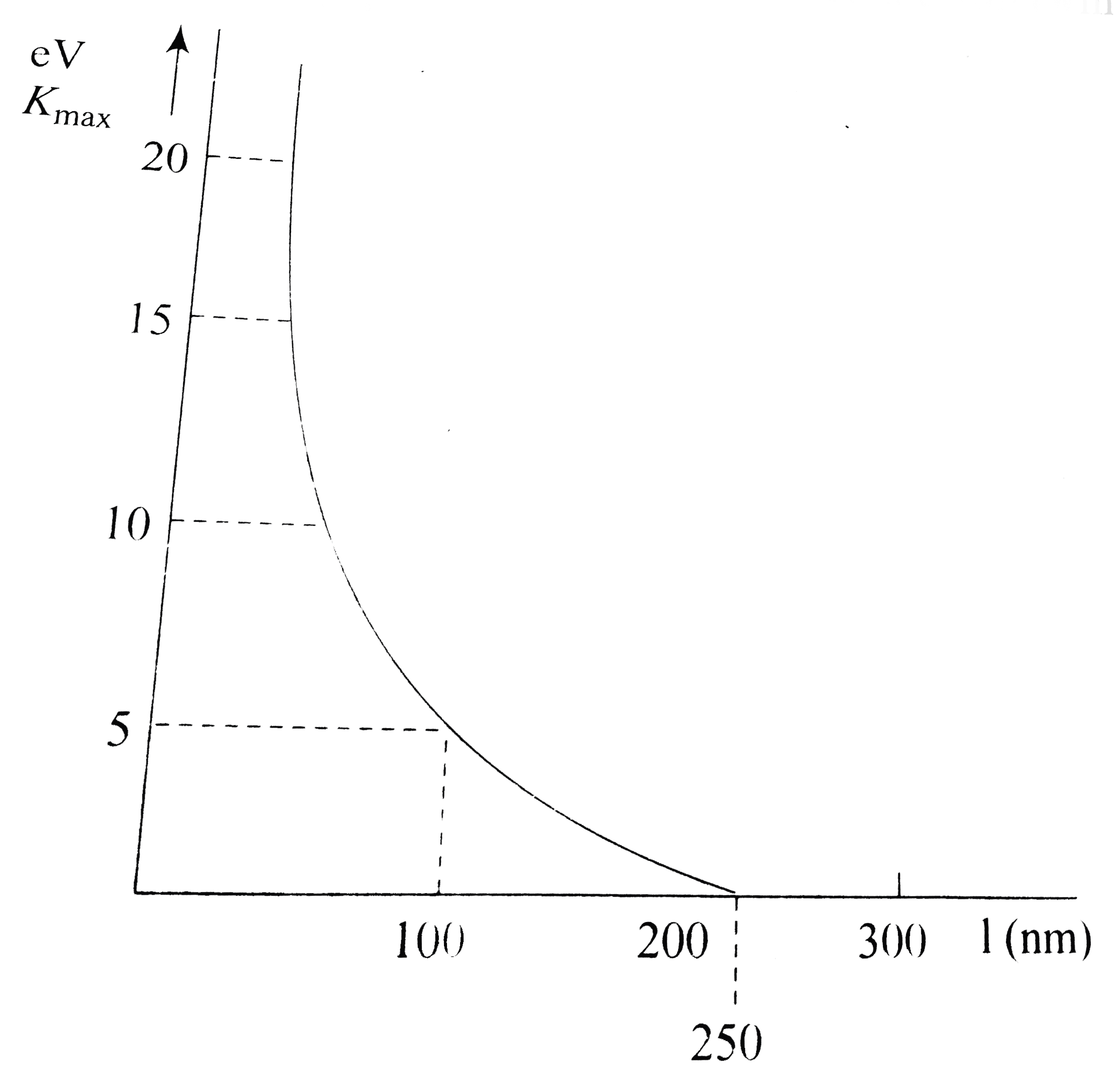
In a photoelectric effect experiment , the maximum kinetic energy of the ejected photoelectrons is measured for various wavelength of the incident light. Figure shows a graph of this maximum kinetic energy Kmax as a function of the wavelength λ of the light falling on the surface of the metal. Which of the following statement/i is/ are correct?
View Solution
