An astronaut is looking down on earth's surface from a space shuttle at an altitude of 400km. Assuming that the astronaut's pupil diameter is 5mm and the wavelength of visible light is 500nm. The astronaut will be able to resolve linear object of the size of about .
0.5m
5m
50m
500m
The correct Answer is:C
The resolving power of the eye is given by
R=1.22λb×D
where λ is the wavelength of light, b is the diameter of the eye lens and D is the distance from the lens at which light is focused.
D=400km=400000m,d=5mm=5×10−3m
λ=500nm=500×10−9m
∴R=1.22×500×10−9×4×1055×10−3=48.8≈50m
Topper's Solved these Questions
Similar Questions
Assume that Rayleigh's criterion gives the limit of resolution of an astronaut's eye looking down on Earth's surface from a typical space shuttle altitude of 420 km. (a) Under that idealized assumption, estimate the smallest linear width on Earth's surface that the astronaut can resolve. Take the astronaut's pupil diameter to be 5 mm and the wavelength of visible light to be 550 nm. (b) Can the astronaut resolve the Great Wall of China, which is more than 3000 km long, 5 to 10 m thick at its base, 4 m thick at its top, and 8 min height? (c) Would the astronaut be able to resolve any unmistakable sign of intelligent life on Earth's surface?

View SolutionThe telescopes on some commercial surveillance satellites can resolve objects on the ground as small as 85 cm across (see Google Earth), and the telescopes on military surveillance satellites reportedly can resolve objects as small as 10 cm across. Assume first that object resolution is determined entirely by Rayleigh's criterion and is not degraded by turbulence in the atmosphere. Also assume that the satellites are at a typical altitude of 420 km and that the wavelength of visible light is 550 nm. What would be the required diameter of the telescope aperture for (a) 85 cm resolution and (b) 10 cm resolution? (c) Now, considering that turbulence is certain to degrade resolution and that the aperture diameter of the Hubble Space Telescope is 2.4 m, what can you say about the answer to (b) and about how the military surveillance resolutions are accomplished?
View Solution
Knowledge Check
The aperrture of the largest telescope in the world is about 5 m. if the separation between the moon and the earth is 4×105km and the wavelength of visible light is 5000 Å, then the minimum separation between the objects on the surface of the moon which can be just resolved is approximately equal to
A200 mB100 mC50 mD25 mTwo luminous point sources separated by a certain distance are at 10 km from an observer. If the aperture of his eye is 2.5×10−3m and the wavelength of light used is 500 nm, the distance of separation between the point sources just seen to be resolved is
A12.2 mB24.2 mC2.44 mD1.22 mThe aperture of the larges telescope in the world is about 5m. If the separation between the moon and the earth is 4×105km and the wavelength of visible light is 6000Å, then minimum separation between the objects on the surface of the moon which can be just resolved is approximately equal to
A29.5mB59 mC88.5 mD1167 m
The two headlights of an approaching automobile are 1.4 m apart. At what (a) angular separation and (b) maximum distance will the eye resolve them? Assume that the pupil diameter is 4.5 mm, and use a wavelength of 550 nm for the light. Also assume that diffraction effects alone limit the resolution so that Rayleigh's criterion can be applied.
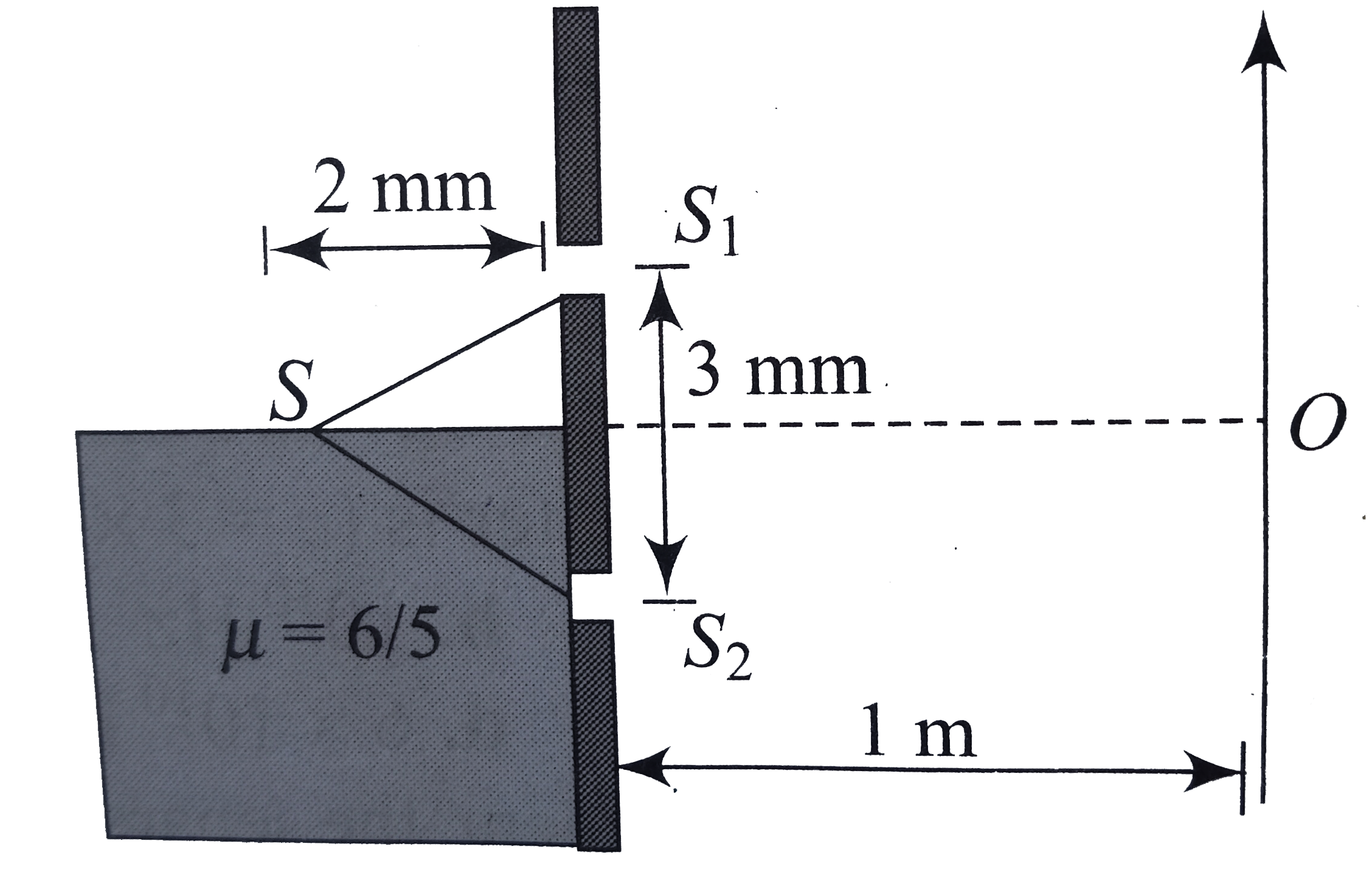
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distance from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
View SolutionA cord of length 64m is used to connected a 100kg astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is 6400km.
View SolutionThe diameter of the pupil of human eye is 2.5 mm. Assuming the wavelength of light used is 5000Å. What must be the minimum distance between two point like objects to the seen clearly if they are a distance of 5 m from the eye?
View SolutionA cord of length 64m is used to connected a 100kg astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is 6400km.
View Solution
