By sucking a straw a student can reduce the pressure in his lungs to of Using the straw, he can drink water from a glass up to a maximum depth of :
10 cm
75 cm
cm
The correct Answer is:C
Pressure difference between lungs and atmosphere =760 mm-750 mm =10 mm 1 cm of Hg.
Pressuire difference of water.
i.e. one can drawn a depth of cm of water
Topper's Solved these Questions
Similar Questions
A body can reduce the pressure in his lungs to 750 mm of mercury. Using a straw he can drink water from a glass upto the maximum depth of _____ cm
(atmospheric pressure = 760 mm of mercury, density of mercury =13.6gcm−3 )
View SolutionA capillary due sealed at the top has an internal radius of r=0.05cm. The tube is placed vertically in water, with its open end dipped in water. Find greatest interger corresponding to the length (in water) of such a tube be for the water in it to rise in these conditions to a height h=1cm ? The pressure The pressure of the air is P0=1atm. =7cm of Hg , density of Hg=13.6/cm3, g=9.8m/sec2 The surface tension of water is σ=70dyne/cm. (assume temperature of air in the tube is constant)
View Solution
Knowledge Check
By sucking a straw a student can reduce the pressure in his lungs 750mm of Hg(density)=13.6g/cm3) Using the straw, he can drink water from a glass up to a maximum depth of :
A10cmB75cmC13.6cmD1.36cmBy sucking through a straw, a student can reduces the pressure in his lungs to 750 mm of Hg (density =13.6g/cm3) Using the straw, he can drink water from a glass upto a maximum depth of :
A10 cmB75 cmC13.6 cmD1.35 cmBy sucking through a straw, a student can reduces the pressure in his lungs to 750 mm of Hg (density =13.6g/cm3) Using the straw, he can drink water from a glass upto a maximum depth of :
A10 cmB75 cmC13.6 cmD1.35 cm
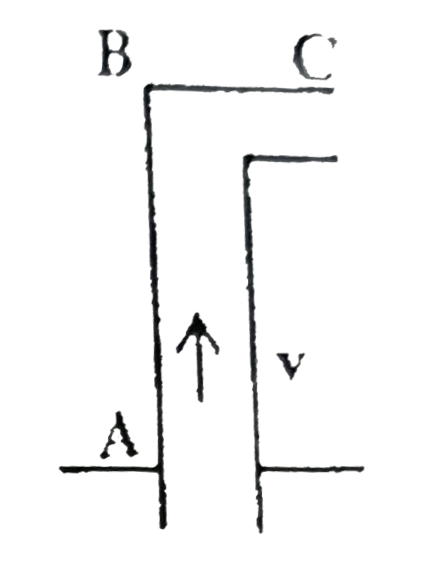
ABC is a light pipe lying in a vertical plane and of cross sectional area 1cm2 whose small part is in ground to fix the pipe. An ideal fluid of density 104kg/m3 is being flown through the pipe by means of external agency. Length of BC can be neglected. The minimum vertical upward force required to pull out the pipe from ground is F=9N. What should be maximum velocity (in m/s) of the fluid so that pipe can not be pulled out from ground ?
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes T1,T2 and T3 are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as x1,x2 and x3 .

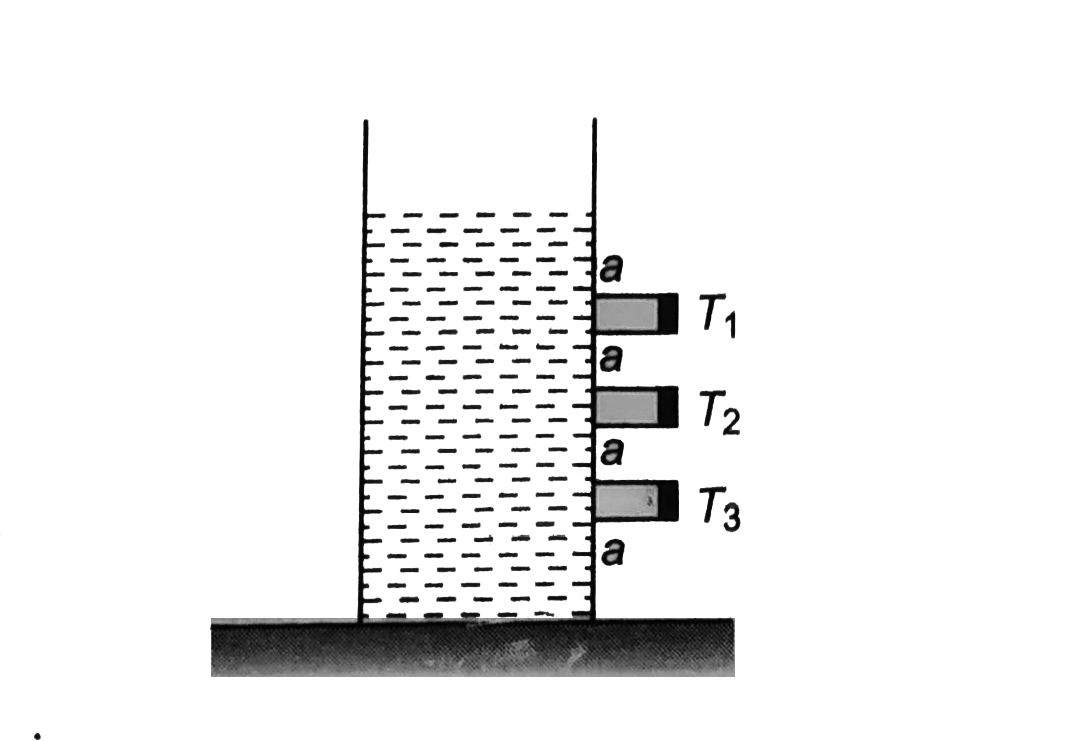
Distance x3 is given by
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes T1,T2 and T3 are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as x1,x2 and x3 .

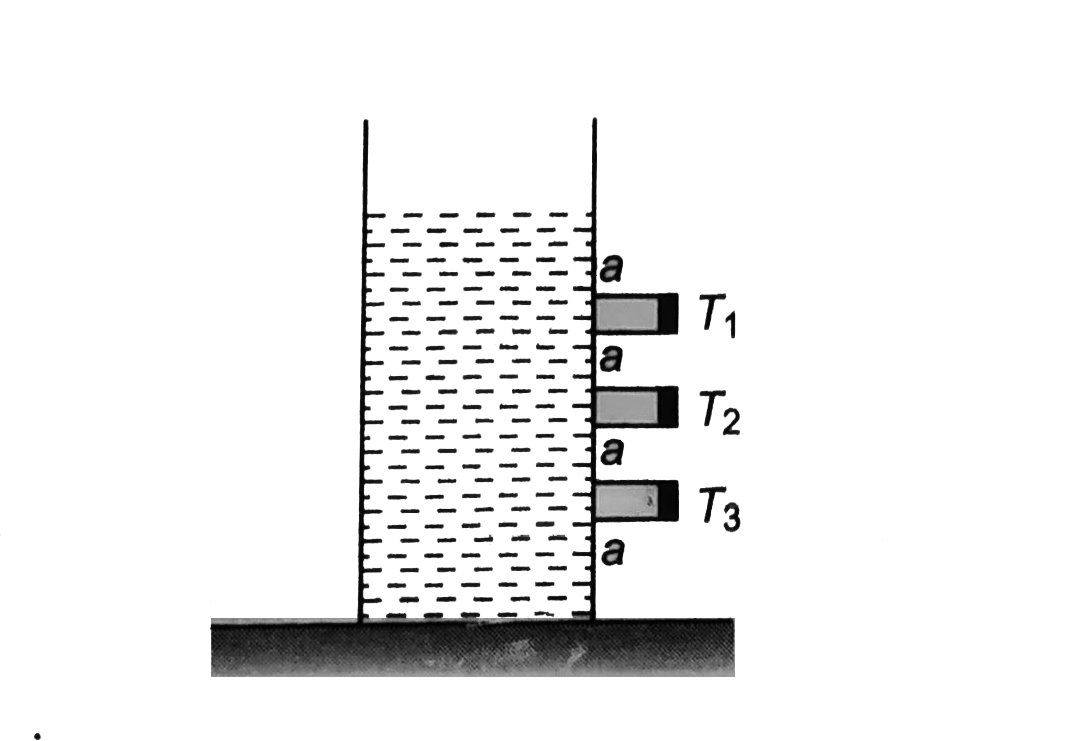
The correct sketch is
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes T1,T2 and T3 are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as (x1),(x2) and (x3) .

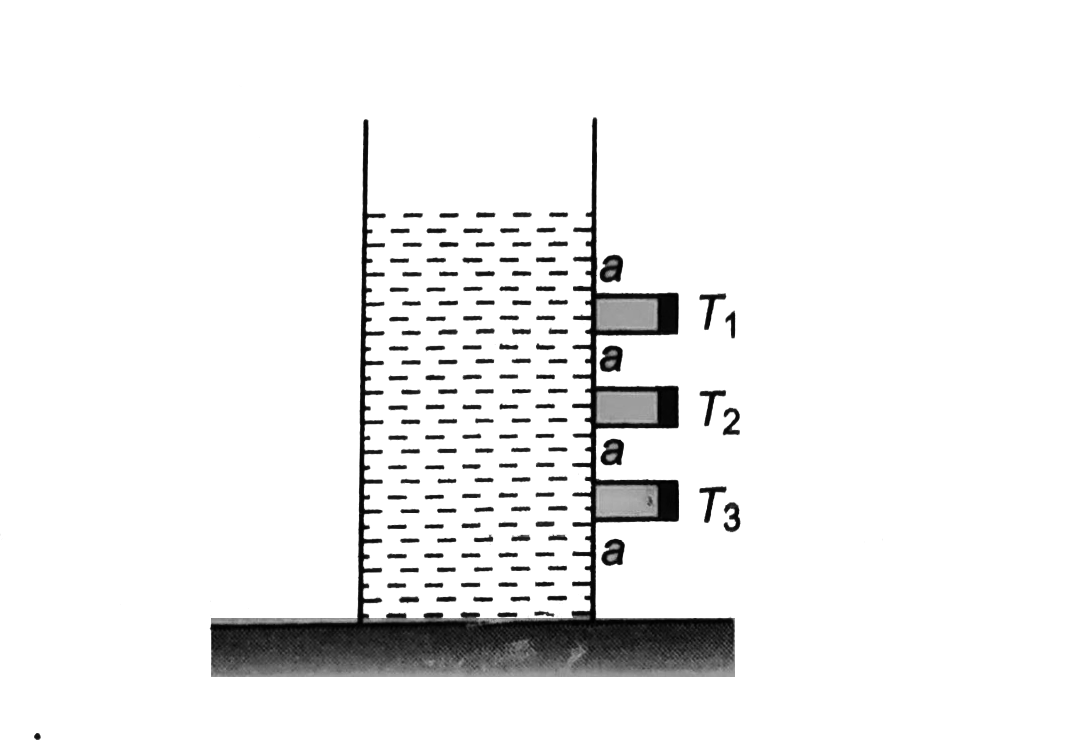
1. speed of efflux is
View Solution
An incompressible liquid is kept in a long conductying cylindrical cantainer, which is closed at its top by an airtight light piston. A cylinder of length 10 cm made of material of density 0.65g/cm3 floats with half-length submerged in the liquid as shown in the figure. Air trapped in the cylinder has density 1.30kg/m3 On placing extra weight on the piston, pressure of the air in the cylinder is increased to 100 times of the initial pressure.What can you conclude? (∵ Use Boyle's law of air i.e., P1V1=P2V2 at constant temperature)
View Solution
