If the water falls from a dam into a turbine wheel 19.6 m below, then the velocity of water at the turbine is $(g = 9.8 m / s^{2})$

A

9.8 m/s

B

19.6 m/s

C

39.2 m/s

D

98.0 m/s

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$v = \sqrt{2 g h} = \sqrt{2 \times 9.8 \times 19.6} = 19.6 m / s$ .

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

BOOK - AIIMS PREVIOUS YEAR PAPERSCHAPTER - AIIMS 2006EXERCISE - PHYSICS
60videos
AIIMS 2006
BOOK - AIIMS PREVIOUS YEAR PAPERSCHAPTER - AIIMS 2008EXERCISE - PHYSICS
60videos
AIIMS 2008

Similar Questions

Knowledge Check

Question 1 - Select One
Water falls from a tap with $A_{0} = 4 m^{2}$ , $A = 1 m^{2}$ and h=2 m, then velocity v is

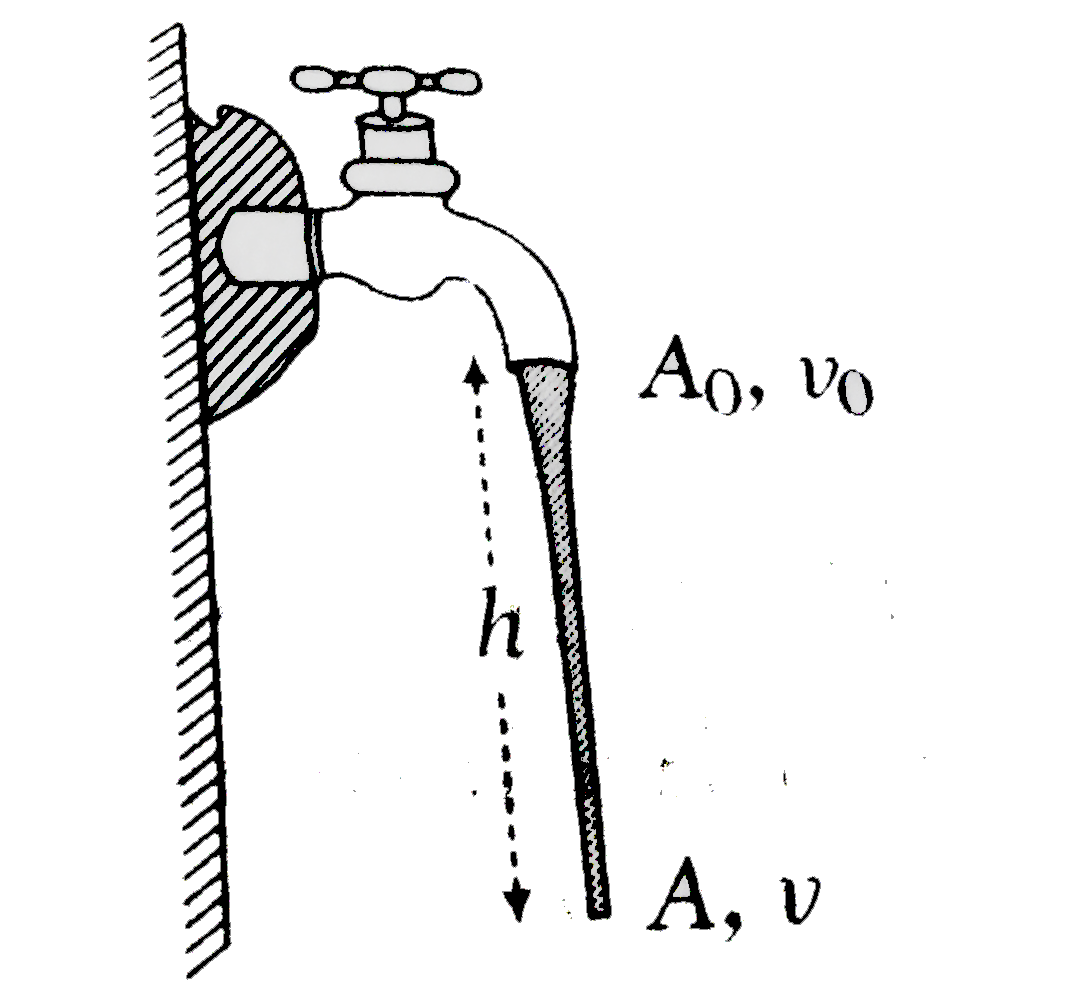A $2.5 m s^{- 1}$
B $6.5 m s^{- 1}$
C $4.5 m s^{- 1}$
D $1.5 m s^{- 1}$
Question 2 - Select One
Water is falling on the blades of a turbine from a height of $25 m$ . $3 \times 10^{3} k g$ of water pours on the blade per minute. If the whole of energy is transferred to the turbine, power delivered is $g = 9.8 m / s^{2}$
A $12250 W$
B $16250 W$
C $8250 W$
D $20250 W$
Question 3 - Select One
Velocity of flow of water in a horizontal pipe is 10.0 m/s. Find the velocity head of water ( $g = 10 m / s^{2}$ )
A9.00m
B5.00 m
C3.00 m
DNone of these

AIIMS PREVIOUS YEAR PAPERS-AIIMS 2007-PHYSICS

Home
Ask Doubt
Profile