Assertion(A) : When sodium chloride dissolves in water, then Na+ and Cl− ions leaving the crystal lattice acquire far greater freedon.
Reason(R ) : In thermodynamic terms, the formation of solution occurs with a favourable change in energy i.e., ΔH has a high positive value and TΔS has a low negative value.
If both assertion and reason are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion
If assertion is true but reasonb is false
If both assertion and reason are false.
The correct Answer is:C
In thermodynamic terms, formation of solution occurs with a favourable change in free energy
ΔG=ΔH−TΔS
where ΔH has a small positive value and TΔS a large positive value, thus ΔG is negative.
Topper's Solved these Questions
Similar Questions
In a ideal crystal there nust be regular repeating arrangement of the constuting particles and its entropy must be zero at absolute zero at absolute zero temperature. However, it is impossible to obtain an ideal crystal and it suffers from certain defects called imperfections. In pure crystal these defects arise either due to disorder or dislocation of the movement of the particles even at absolute zero temperature. Such defect increases with rise in temperature. In addition ti this, certain defects arise due to the pressure of some impurities. Such defects not only modify the existing properties of the crystalline solid but also impart certain new characteritics to them.
In pure crystal, e.g, silicon or germanium at 0K, the electrons are prsent in fully occupied lowest energy states and are not xpected to conduct any electricity. However at temperature above 0K, some electron leave their bonds and become free to move in the crystal lattice, giving rise to and become free to move in the crystal lattice, giving rise to electrical conductivity. The electron deficient bonds, called holes (+vely charged) and thermally mobile electrons move in opposite direction under the electric field.
Stoichiometric ppoint defects include (a) Schottky defects, which arise due to missing of both cations and anions from their lattice sites without disturbing the stoichiometry and
(b) Frenked defects, which arise due to misplacement of certian ions in the crystal lattice. The former defect gives rise to no change of density.
Another type of defects are non-stoichometry defects where the cetions and anion are not present in the stoichiometry ratio. In metal excess defect, metal ions or positive ions are in excess as compared to anions of non-metals stoichiometrycally. On the other hand in metal deficiency defect, the cations are in lesser proportion than stoichiometric value. Since the crystal is neutral electrically, the balance of charge is maintained by free electrons or extra positive charges. The metal excess defects gives rise to conduction of electricity due to the presence of free electrons. Also crystals having metal excess defects are paramagnetic and coloured due to the presence of electrons in the anion vacancies.
Impurity defects arise when some foreign atoms are present at the lattice sites in place of the host atoms or at the vacant interstitial sites.
When 15 group elements like P or are doped into Si or Ge, the added impurity atoms occupy the lattice sites forming four covalent bonds with 4 Si/Ge atoms leaving an extra electron free to move. Such a crystal is said to be n-type semi conductor because the conduction of electricity is due to movement of extra unbounded electrons.
If doping of a covalent crystal of 14 group elements are caused by addition of small amounts of elements are caused by addition of small amounts of elements of group 13, e.g, Al or Ga with three valence electrons, one covalent bond formed will be electron deficient and acts as a positive hole. The presence of such holes in the crystal leads to electrical conductivity and the the crystal is said to be p-type semiconductor.
In the crystal of Fe0.93 O, the percentage of Fe(III) will be:View SolutionIn a ideal crystal there nust be regular repeating arrangement of the constuting particles and its entropy must be zero at absolute zero at absolute zero temperature. However, it is impossible to obtain an ideal crystal and it suffers from certain defects called imperfections. In pure crystal these defects arise either due to disorder or dislocation of the movement of the particles even at absolute zero temperature. Such defect increases with rise in temperature. In addition ti this, certain defects arise due to the pressure of some impurities. Such defects not only modify the existing properties of the crystalline solid but also impart certain new characteritics to them.
In pure crystal, e.g, silicon or germanium at 0K, the electrons are prsent in fully occupied lowest energy states and are not xpected to conduct any electricity. However at temperature above 0K, some electron leave their bonds and become free to move in the crystal lattice, giving rise to and become free to move in the crystal lattice, giving rise to electrical conductivity. The electron deficient bonds, called holes (+vely charged) and thermally mobile electrons move in opposite direction under the electric field.
Stoichiometric ppoint defects include (a) Schottky defects, which arise due to missing of both cations and anions from their lattice sites without disturbing the stoichiometry and
(b) Frenked defects, which arise due to misplacement of certian ions in the crystal lattice. The former defect gives rise to no change of density.
Another type of defects are non-stoichometry defects where the cetions and anion are not present in the stoichiometry ratio. In metal excess defect, metal ions or positive ions are in excess as compared to anions of non-metals stoichiometrycally. On the other hand in metal deficiency defect, the cations are in lesser proportion than stoichiometric value. Since the crystal is neutral electrically, the balance of charge is maintained by free electrons or extra positive charges. The metal excess defects gives rise to conduction of electricity due to the presence of free electrons. Also crystals having metal excess defects are paramagnetic and coloured due to the presence of electrons in the anion vacancies.
Impurity defects arise when some foreign atoms are present at the lattice sites in place of the host atoms or at the vacant interstitial sites.
When 15 group elements like P or are doped into Si or Ge, the added impurity atoms occupy the lattice sites forming four covalent bonds with 4 Si/Ge atoms leaving an extra electron free to move. Such a crystal is said to be n-type semi conductor because the conduction of electricity is due to movement of extra unbounded electrons.
If doping of a covalent crystal of 14 group elements are caused by addition of small amounts of elements are caused by addition of small amounts of elements of group 13, e.g, Al or Ga with three valence electrons, one covalent bond formed will be electron deficient and acts as a positive hole. The presence of such holes in the crystal leads to electrical conductivity and the the crystal is said to be p-type semiconductor.
The type of semiconduction shown by crystal capable of showing Schottky defect, will be :View Solution
Knowledge Check
- Question 1 - Select One
For a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
A reaction has a value of ΔH=-40 kcal at 400K . Above 400K, the reaction is spontaneous, below this temperature, it is not. The value of ΔG and ΔS at 400K are respectively:A0,−0.1,calK−1B0,100calK−1C−10kcal,−100calK−1D0,−100calK−1 - Question 2 - Select One
For a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
The enthalpy change for a certain reaction at 300K is -15.0 k cal mol−1 . The entropy change under these conditions is -7.2 cal K−1mol−1. The free energy change for the reaction and its spontaneous/non-spontaneous character will be :A−12.84 kcal mol−1, spontaneousB12.84 kcal mol−1, non-spontaneousC−17.16kcal mol−1,spontaneousDnone of the above - Question 3 - Select One
For a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
When CaCO3 is heated to a high temperature, it undergoes decomposition into CaO and CO2 whereas it is quite stable at room temperature. The most likely explanation of it, is:Athe enthalpy of reaction (ΔH) outweighs the term TΔS at high temperatureBthe term TΔS outweighs the enthalpy of reaction at high temperatureCat high temperature, both enthalpy of reaction and entropy change become negativeDnone of the above
For a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 298K, 2A+B→C ΔH=100 kcal and ΔS=0.050 kcal K−1. If ΔH and ΔS are assumed to be constant over the temperature range, just above what temperature will be reaction become spontaneous?View SolutionFor a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction 25∘C,X2O2(l)→2XO2(g) ΔH=2.1 kcal and ΔS=20 cal K−1 . The reaction would be:View SolutionCrystal field theory views the bonding in complexes as arising from electrostatic interaction and considers the effect of the ligand charges on the energies of the metal ion d-orbitals
In this theory, a ligand lone pair is modelled as a point negative charge that repels electrons in the d-orbitals of the central metal ion.The theory concentrated on the resulting splitting of the d-orbitals in two groups with different energies and used that splitting to rationalize and correlate the optical spectra,thermodynamic stability, and magnetic properties of complexes.This energy splitting between the two sets of d-orbitals is called the crystal field splitting Δ.
In general, the crystal field splitting energy Δ corresponds to wavelenght of light in visible region of the spectrum, and colours of the complexes can therefore be attributed to electronic transition between the lower and higher energy sets of d-orbitals.
In general, the colour that we see is complementry to the colour absorbed.

Different metal ions have different value of Δ, which explains why their complexes with the same ligand have different colour.
Similarly the crystal field splitting also depends on the nature of ligands and as the ligand for the same metal varies from H2O to NH3 to ethylenediamine, Δ for complexes increase.Accordingly, the electronic transition shifts to higher energy (shorter wavelength) as the ligand varies from H2O from NH3 to en, thus accounting for the variation in colour.
Crystal field theory accounts for the magnetic properties of complexes in terms of the relative values of Δ and the spin pairing energy P. Small Δ values favour high spin complexes, and large Δ values favour low spin complexes.
The [Ti(NCS)6]3− ion exhibits a single absorption band at 544 nm.What will be the crystal field splitting energy (in kJ mol−1) of the complex ? (h=6.626×10−34J.s,C=3.0×105m/s,NA=6.02×1023 ions/mole.View SolutionCrystal field theory views the bonding in complexes as arising from electrostatic interaction and considers the effect of the ligand charges on the energies of the metal ion d-orbitals
In this theory, a ligand lone pair is modelled as a point negative charge that repels electrons in the d-orbitals of the central metal ion.The theory concentrated on the resulting splitting of the d-orbitals in two groups with different energies and used that splitting to rationalize and correlate the optical spectra,thermodynamic stability, and magnetic properties of complexes.This energy splitting between the two sets of d-orbitals is called the crystal field splitting Δ.
In general, the crystal field splitting energy Δ corresponds to wavelenght of light in visible region of the spectrum, and colours of the complexes can therefore be attributed to electronic transition between the lower and higher energy sets of d-orbitals.
In general, the colour that we see is complementry to the colour absorbed.
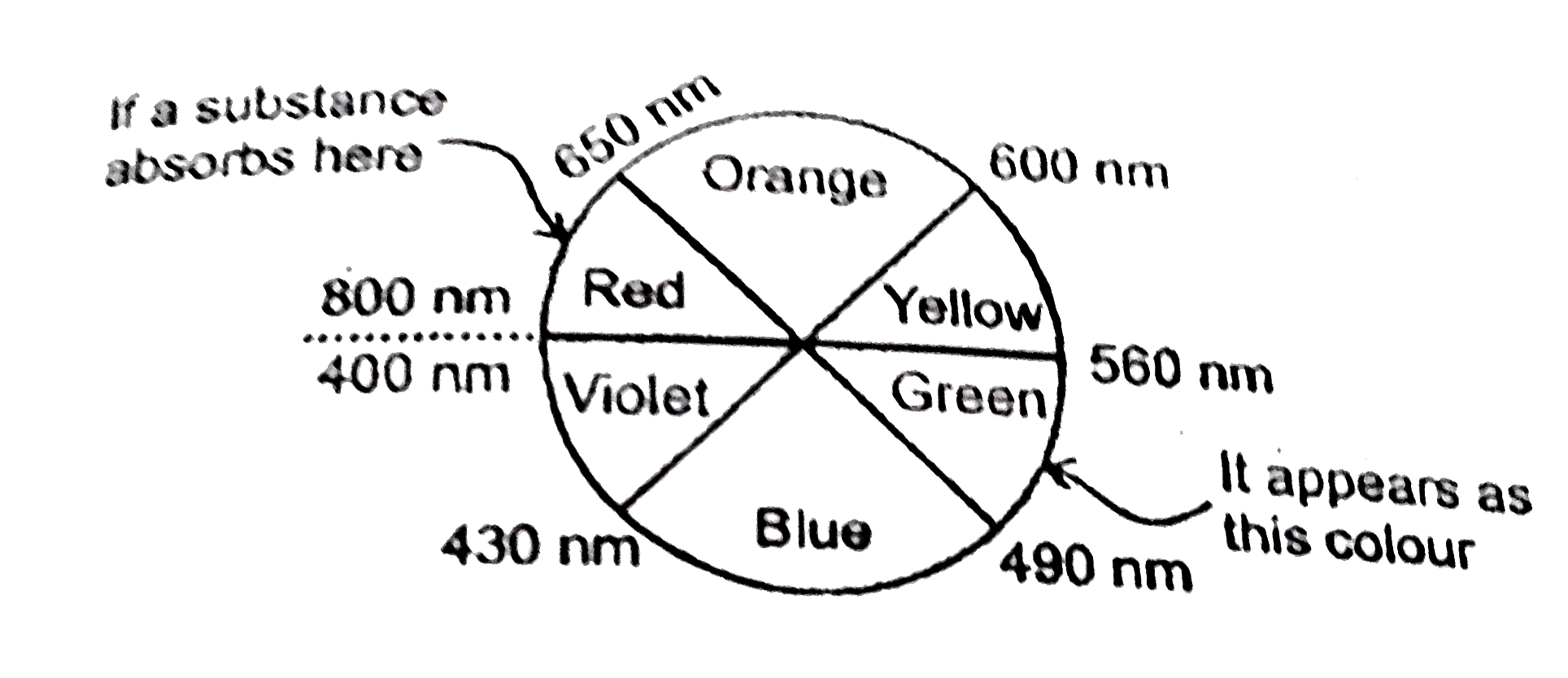
Different metal ions have different value of Δ, which explains why their complexes with the same ligand have different colour.
Similarly the crystal field splitting also depends on the nature of ligands and as the ligand for the same metal varies from H2O to NH3 to ethylenediamine, Δ for complexes increase.Accordingly, the electronic transition shifts to higher energy (shorter wavelength) as the ligand varies from H2O from NH3 to en, thus accounting for the variation in colour.
Crystal field theory accounts for the magnetic properties of complexes in terms of the relative values of Δ and the spin pairing energy P. Small Δ values favour high spin complexes, and large Δ values favour low spin complexes.
Which of the following complexes are diamagnetic ?
[Pt(NH3)4]2+[Co(SCN)4]2−[Cu(en)2]2+[HgI4]2−square planartetrahedralsquare planartetrahedral(i)(ii)(iii)ivView SolutionCrystal field theory views the bonding in complexes as arising from electrostatic interaction and considers the effect of the ligand charges on the energies of the metal ion d-orbitals
In this theory, a ligand lone pair is modelled as a point negative charge that repels electrons in the d-orbitals of the central metal ion.The theory concentrated on the resulting splitting of the d-orbitals in two groups with different energies and used that splitting to rationalize and correlate the optical spectra,thermodynamic stability, and magnetic properties of complexes.This energy splitting between the two sets of d-orbitals is called the crystal field splitting Δ.
In general, the crystal field splitting energy Δ corresponds to wavelenght of light in visible region of the spectrum, and colours of the complexes can therefore be attributed to electronic transition between the lower and higher energy sets of d-orbitals.
In general, the colour that we see is complementry to the colour absorbed.
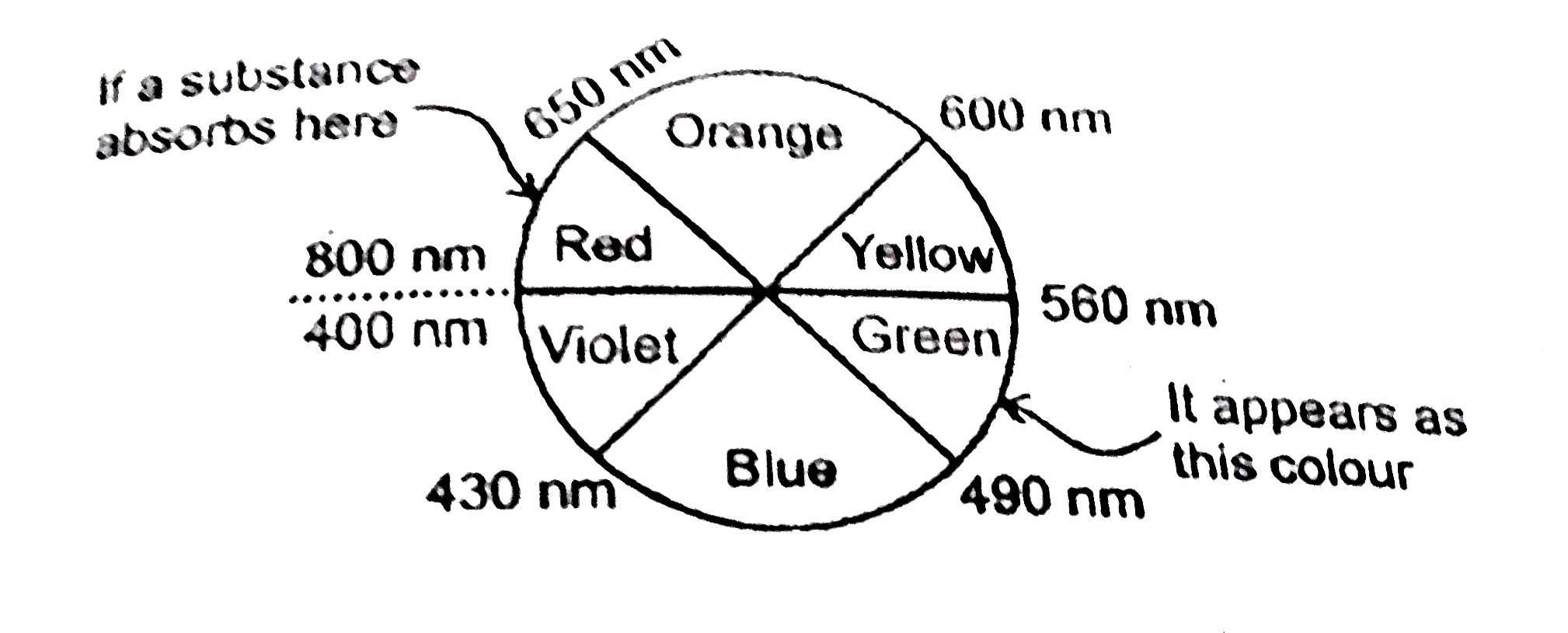
Different metal ions have different value of Δ, which explains why their complexes with the same ligand have different colour.
Similarly the crystal field splitting also depends on the nature of ligands and as the ligand for the same metal varies from H2O to NH3 to ethylenediamine, Δ for complexes increase.Accordingly, the electronic transition shifts to higher energy (shorter wavelength) as the ligand varies from H2O from NH3 to en, thus accounting for the variation in colour.
Crystal field theory accounts for the magnetic properties of complexes in terms of the relative values of Δ and the spin pairing energy P. Small Δ values favour high spin complexes, and large Δ values favour low spin complexes.
Which of the following statements is incorrect ?View Solution

