Electric field at centre of a uniforly charged semicirlce of radius a is
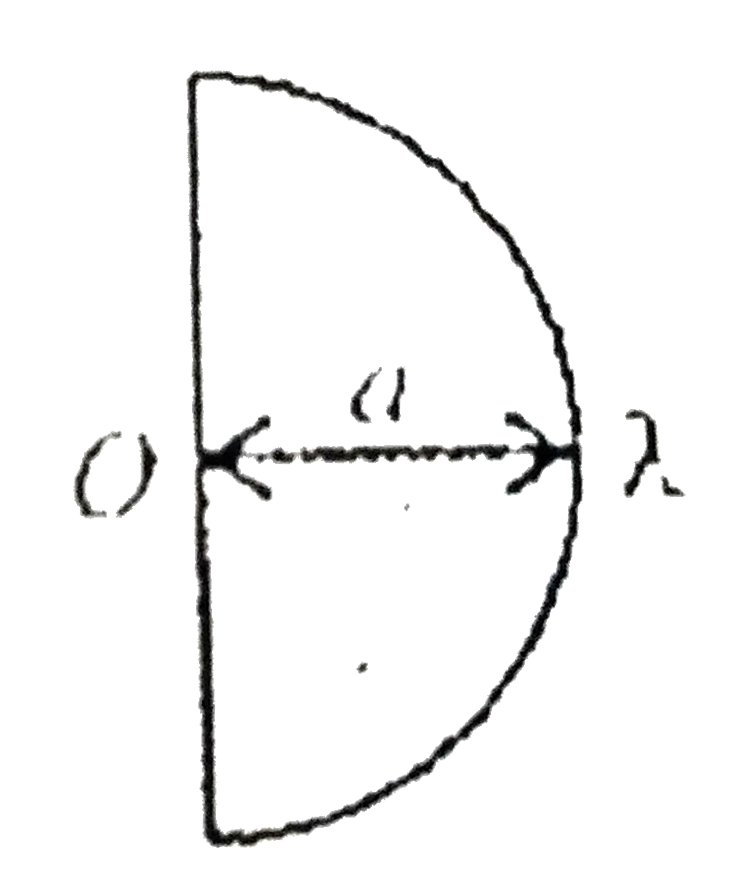
λ2πε0a3
λ2πε0a2
λ22πε0a
λ2πε0a
The correct Answer is:D
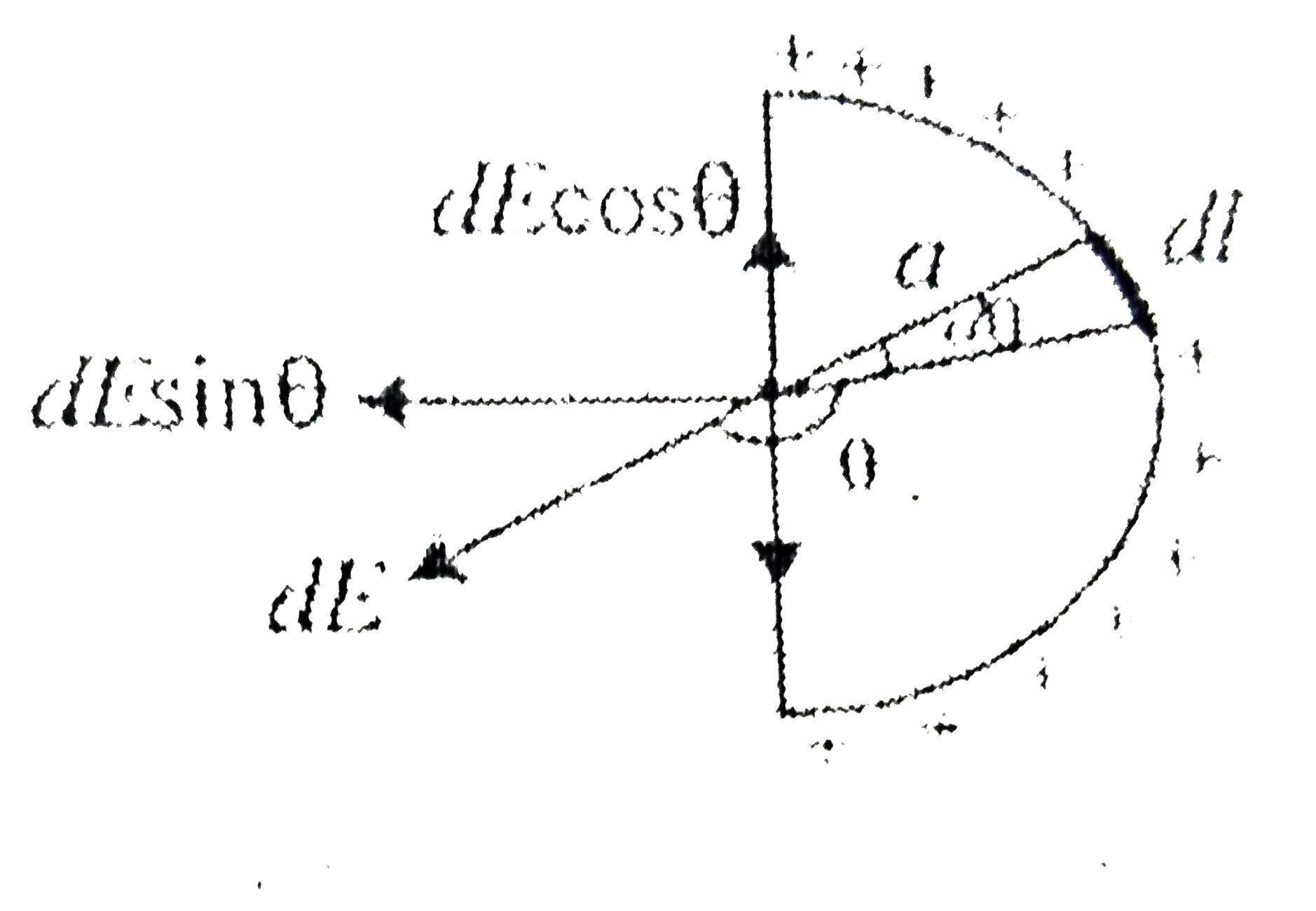
Electtric field intensity at O due to small elemental length dl of charged ring .
dE=14πε0⋅λdla2=14πε0⋅λadθa2
dE=14πε0⋅λadθ
∴ Net electric field at centre O is
E = ∫dEsinθ=π∫014πε0λasinθdθ
=λ4πε0a[−cosθ]π0
∴E=λ2πε0a.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπR - Question 2 - Select One
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A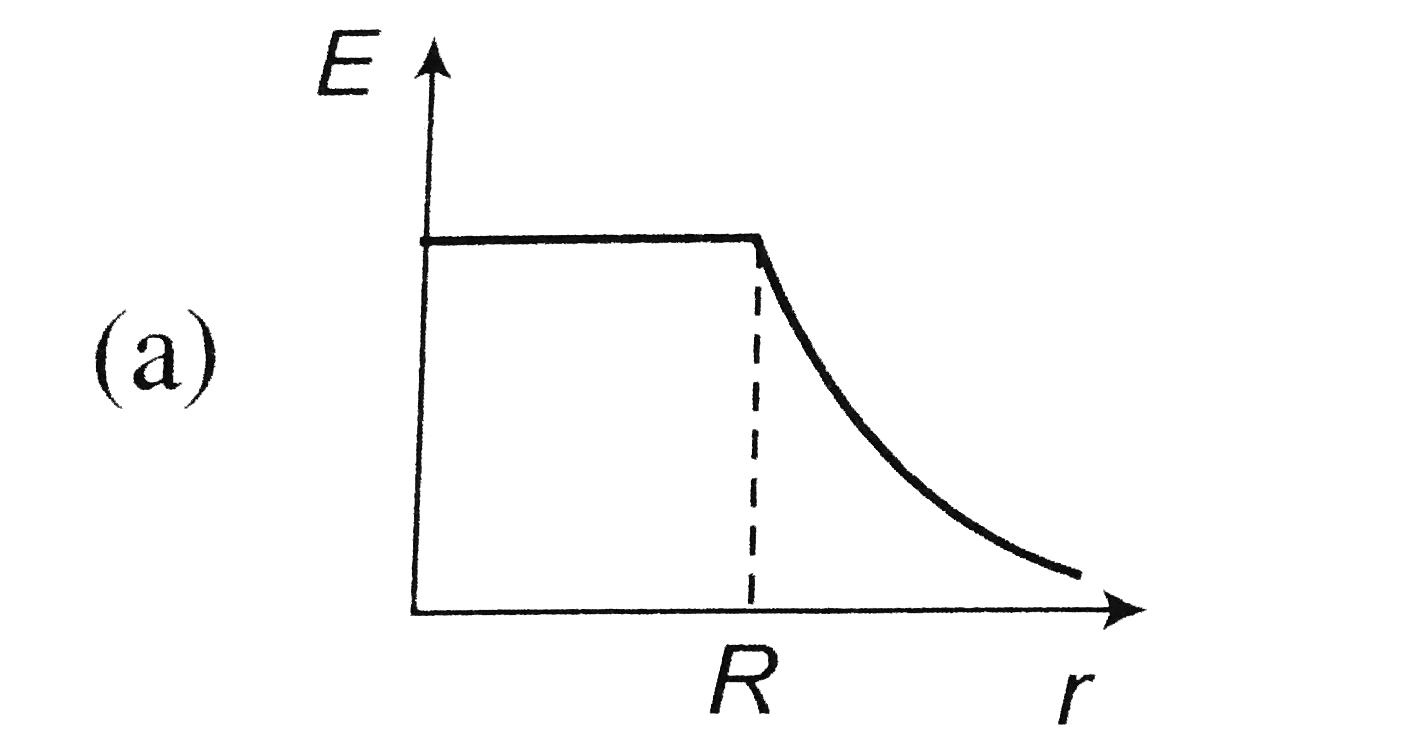 B
B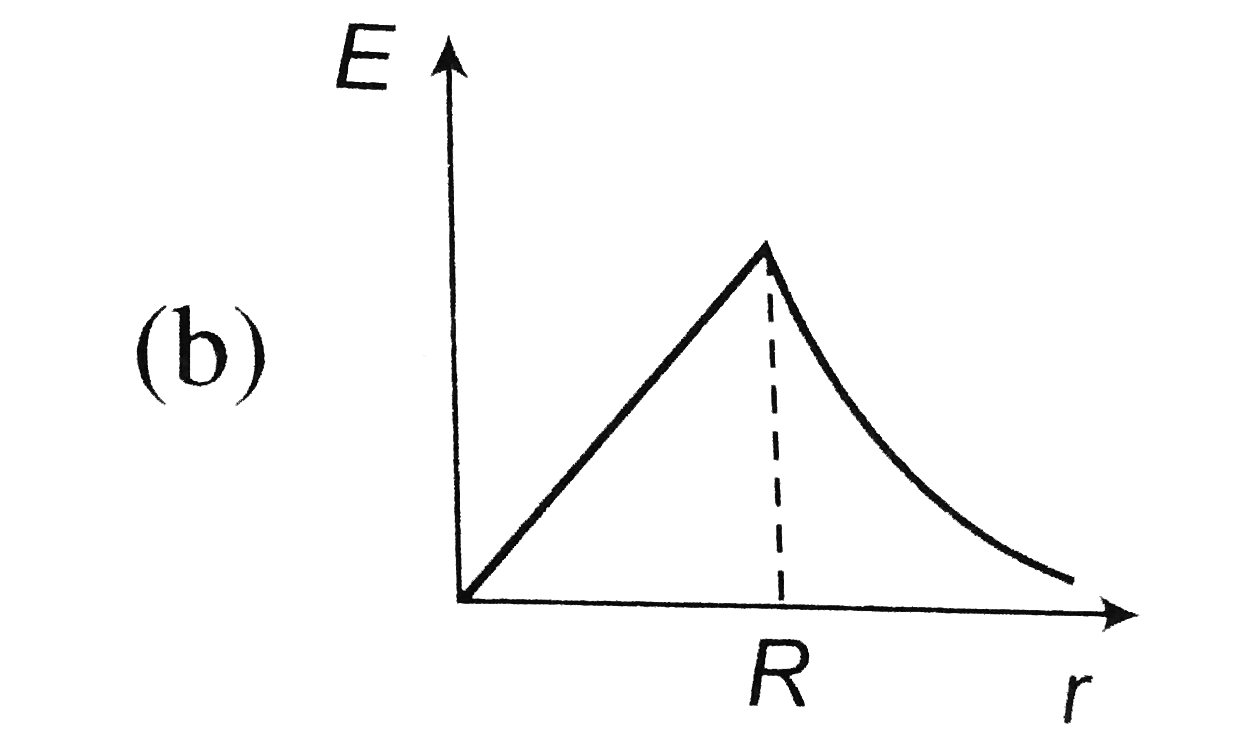 C
C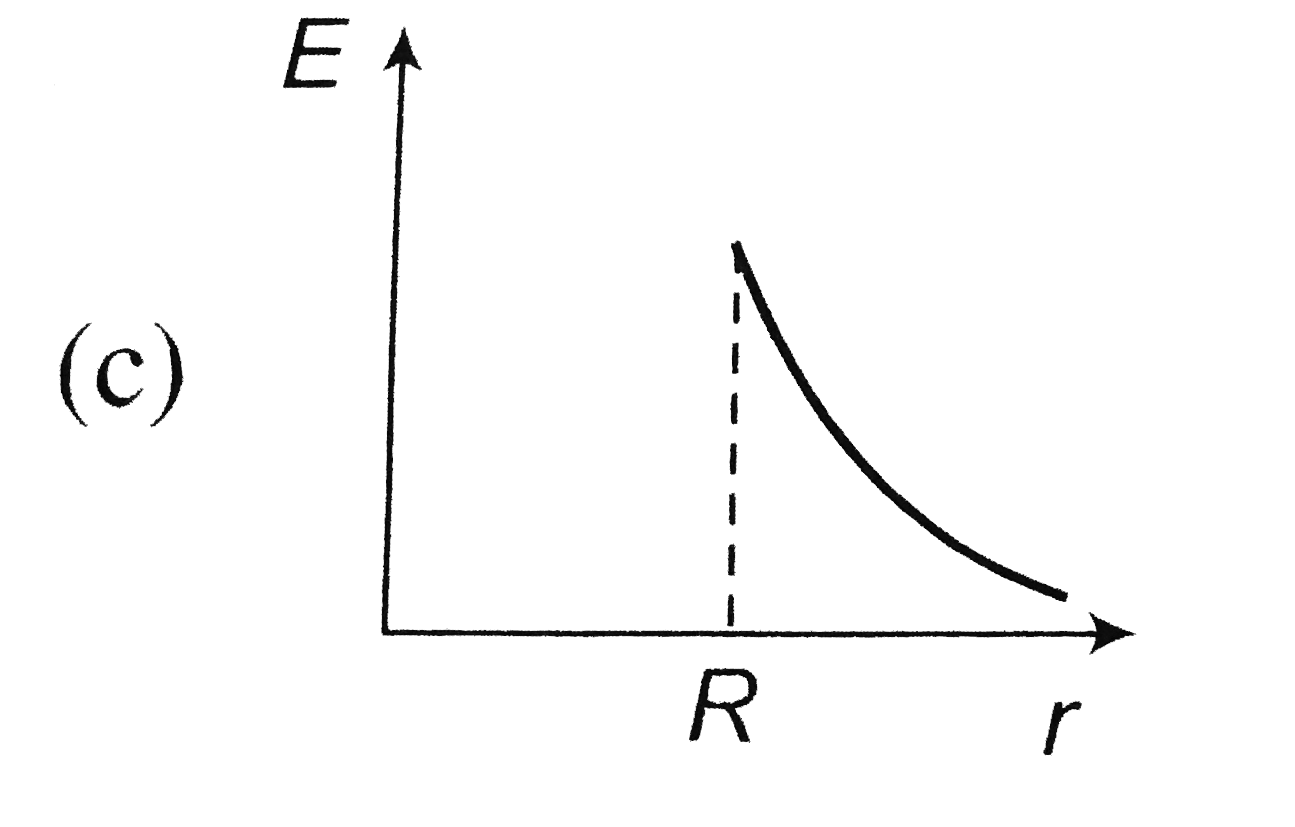 D
D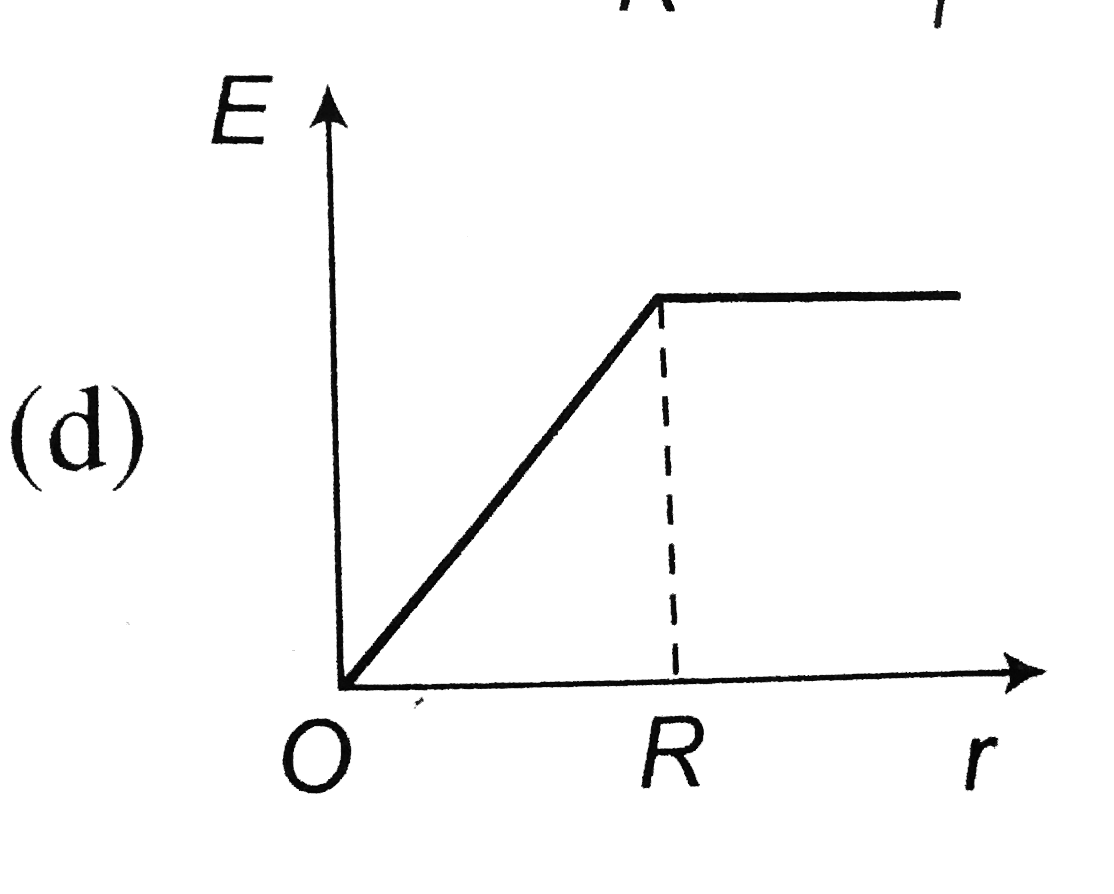
- Question 3 - Select One
At which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?
AR√2BR√3C√2RD√3R
Graphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
View SolutionAt a point 20cm from the centre of a uniformly charged dielectric sphere of radius 10cm, the electric field is 100V/m. The electric field at 3cm from the centre of the sphere will be
View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View SolutionAssertion: Electric potential on the surface of a charged sphere of radius R is V. Then electric field at distance r=R2 from centre is V2R. Charge is distributed uniformly over the volume.
Reason: From centre to surface, electric field varies linearly with r. Here r is distance from centre.View Solution


