A block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
μmgdcosθ+μsinθ
μmgdcosθcosθ+μsinθ
μmgdsinθcosθ+μsinθ
μmgdcosθcosθ−μsinθ
The correct Answer is:B
Because the block moves with a uniform velocity, the resultant force is zero. Resolving F into horizontl component F cosθ and vertical component Fsinθ , we get
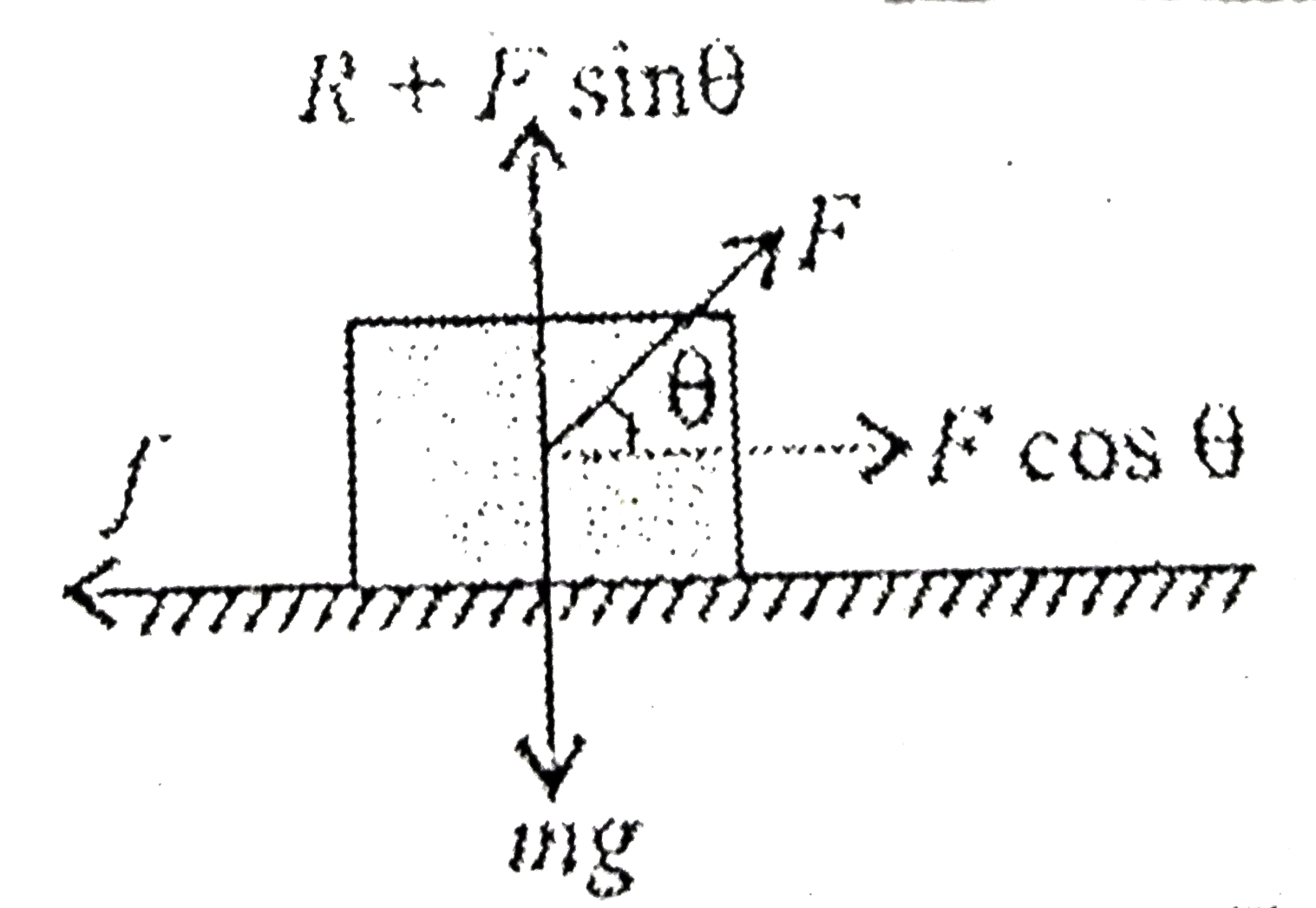
R+Fsinθ=mgorR=mg−Fsinθ
Also f=μR=μ(mg−Fsinθ)
But Fcosθ=f
or Fcosθ=μ(mg−Fsinθ)
or F(cosθ+μsinθ)=μmg
∴F=μmgcosθ+μsinθ
Work W = Fs cosθ
∴W=μmgdcosθcosθ+μsinθ
(∵s=d)
Topper's Solved these Questions
Similar Questions
A block of mass 5 kg is pulled along a horizontal. The friction coefficient between the block and the surface is 0.5. If the block travels at constant velocity, find the work done by this applied force during a displacement 4 m of the block.
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
Aμmgdcosθ+μsinθBμmgdcosθcosθ+μcosθCμmgdsinθcosθ+μsinθDμmgdcosθcosθ−μsinθ - Question 2 - Select One or More
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreases - Question 3 - Select One
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ
A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View SolutionA block of weight 200N is pulled along a rough horizontal surface at constant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is
View SolutionA block of weight 200N is pulled along a rough horizontal surface at contant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is .
View Solution

