A needle of length l m and mass m kg is placed horizontal on wter surface habing surface tension T Find T in terms of m, l (g acceleration due to gravity)
T=mg2l
T=mgl
T=3mg2l
T=m2l
The correct Answer is:A
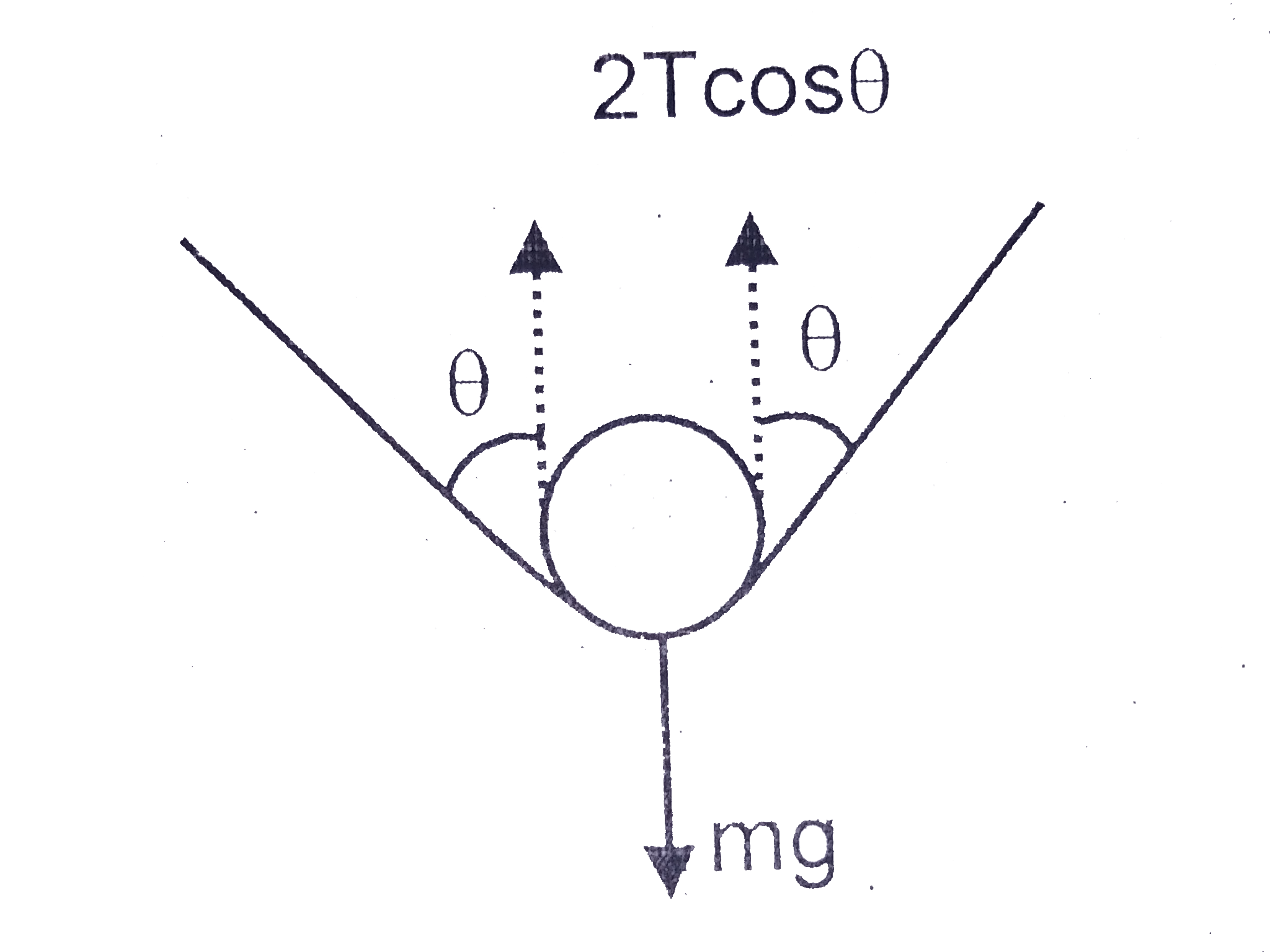
2Tcosθ=mg
T=mg2cosθ
θ is very
T=mg2l
Topper's Solved these Questions
Similar Questions
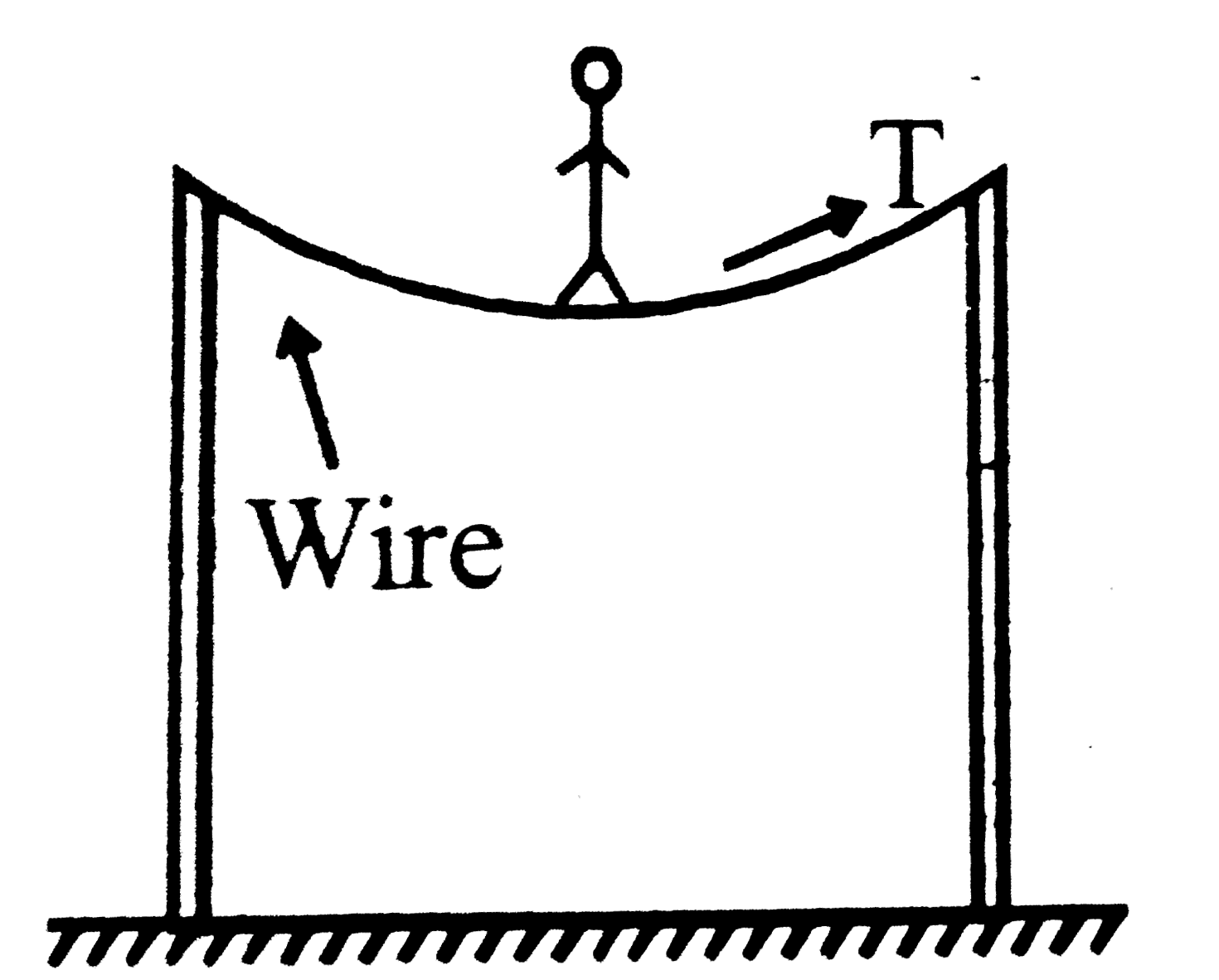
A circus performer of mass M is walking along a wire as shown in the figure given above. The tension T in the wire is (g = acceleration due to gravity)View SolutionA point mass m, is placed at the surface of a hypothetical planet where acceleration due to gravity is g2, where g acceleration due to gravity at the poles the planet. The latitude of that position is [T is time period of planet rotation about its own axis and R is radius of planet]
View Solution
Knowledge Check
- Question 1 - Select One
The binding energy of an object of mass m placed on the surface of the earth r is (R = radius of earth, g = acceleration due to gravity)
AmgR/2Bmg RCmgR4DmgR8 - Question 2 - Select One
A satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of g0, the value of acceleration due to gravity at the earth's surface,
A2mg0R2R+hB−2mg0R2R+hCmg0R22(R+h)D−mg0R22(R+h) - Question 3 - Select One
A simple pendulum of length 'L' has mass 'M' and it oscillates freely with amplitude energy is
(g = acceleration due to gravity)AMgA22LBMgA2LCMgA2LD2MgA2L
A particle of mass 'm' is raised to a height h=R from the surface of earth. Find increase in potential energy. R= radius of earth. g= acceleration due to gravity on the surface of earth.
View SolutionA satellite of mass m is orbiting the earth of radius R at) a height h from its surface. The total energy of the satellite in terms of g0 the value of acceleration due to gravity at the earth 's surface, is
View SolutionTwo masses m and m' are tied with a thread passing over a pulley, m' is on a frictionless horizontal surface and m is hanging freely. If acceleration due to gravity is g, the acceleration of m' in this arrangment will be :
View SolutionThe surface tension is T=Fl, then the dimensions of surface tension is
View SolutionFind the acceleration due to gravity on the surface of the moon by taking a seconds pendulum from the earth's surface. Arrange the following steps in sequential order to solvbe the above problem.
(A) Find the time period of this simple pendulum on the surface of the moon using a stop clock [TM]
(B) The acceleration due to gravity on the moon (gm) is 1/6th the accleration due to gravity on the earth (ge).
(C) Use the formula , T=2π√lg
(D) first , take pendulum to the surface of the moon without altering the length of the pendulum (l), .
(E) Substibe the value of TM in (a), then TETM√gMgE, and obtain the value of (gm)View Solution

