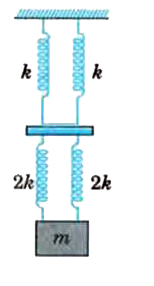As shown in figure in a simple harmonic motion oscillator having identical four springs has time period

T=2π√m4k
T=2π√m2k
T=2π√mk
T=2π√m8k
The correct Answer is:C
Step by step video, text & image solution for As shown in figure in a simple harmonic motion oscillator having identical four springs has time period by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
As shown in figure in a simple barmonic motion obscillator having identical four springs has time period
 AT=2π√m4kBT=2π√m2kCT=2π√mkDT=2π√m8k
AT=2π√m4kBT=2π√m2kCT=2π√mkDT=2π√m8k - Question 2 - Select One
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The maximum speed of junction P is V0. Assume springs are massless. Select the correct option/s
 AAmplitude of potential energy is springs S1 and S2 is respectivley 19kA2 and kA2BAmplitude of potential energy is S1 and S2 is respectively 29kA2 and 19kA2CV0=A√8k27MDV0=A√8k81M
AAmplitude of potential energy is springs S1 and S2 is respectivley 19kA2 and kA2BAmplitude of potential energy is S1 and S2 is respectively 29kA2 and 19kA2CV0=A√8k27MDV0=A√8k81M - Question 3 - Select One
The acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
A4π√3sB2π√3sCThe given graph doesn't represent simple harmonic motionDinformation is insufficient
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-
 View Solution
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
View SolutionA particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part isused to continue the simple harmonic motion, the time period will
View SolutionA ball is rolling without slipping in a spherical shallow bowl (radius R) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, the period of oscillation
 View Solution
View SolutionAssertion : Time period of a simple harmonic oscillator depends on amplitude and force cosntant
Reason : Frequency of a simple harmonic oscillatior is determined by tis elasticity and inertia .View Solution