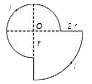
Consider the circullar loop having current I and with central point O. The magnatic field at the central point O is

2μ0i3πR acting downward
5μ0i12R acting downward
6μ0i11R acting downward
3μ0i7R acting upaward
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the circular loop having current I and with central point O. the magnetic field at the central point O is
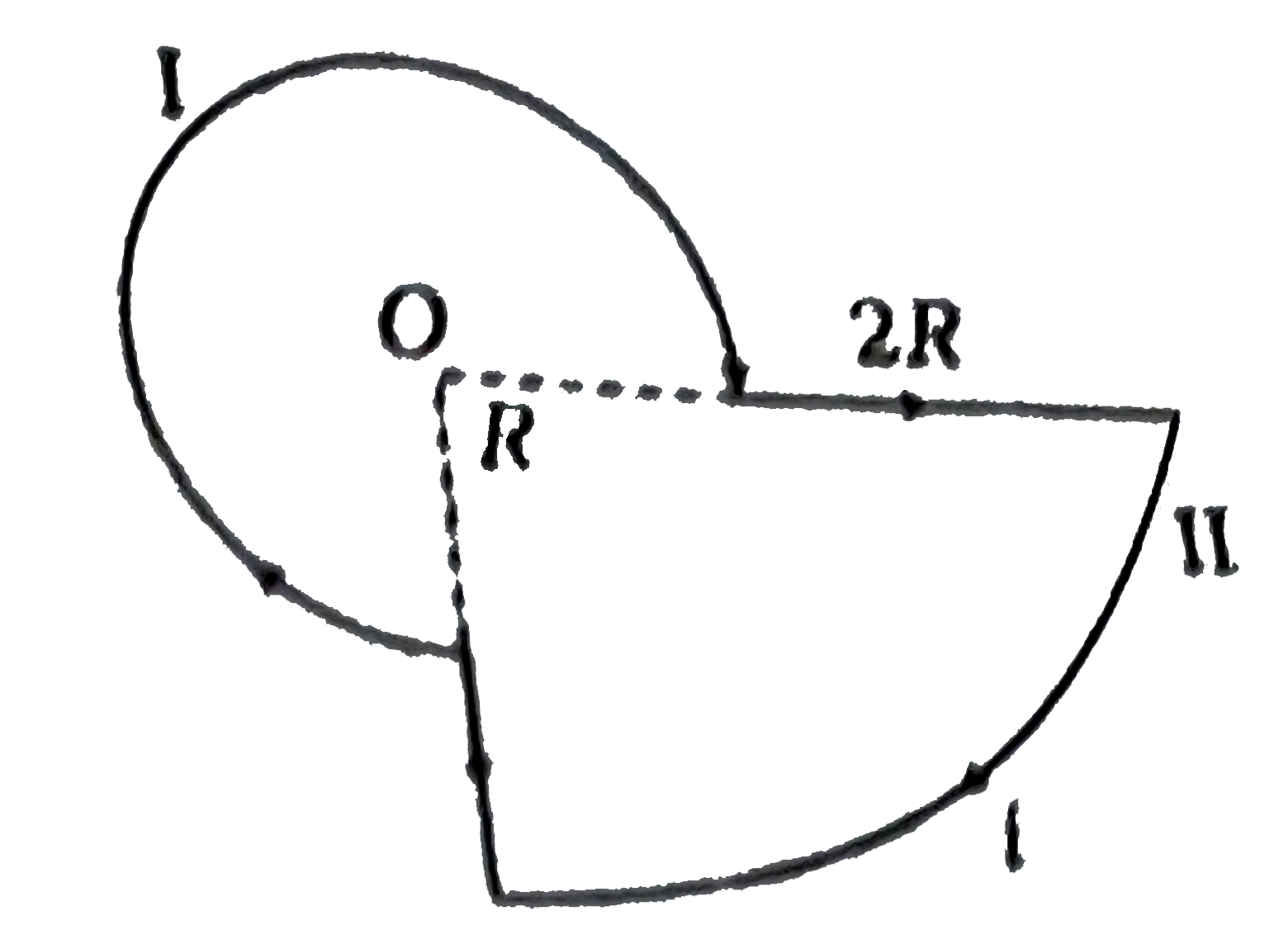 A2μ0i3πR acting downwardB5μ0i12R acting downwardC6μ0i11R acting downwardD3μ0i7R acting downward
A2μ0i3πR acting downwardB5μ0i12R acting downwardC6μ0i11R acting downwardD3μ0i7R acting downwardO is mid-point of AB. The magnetic field at O is
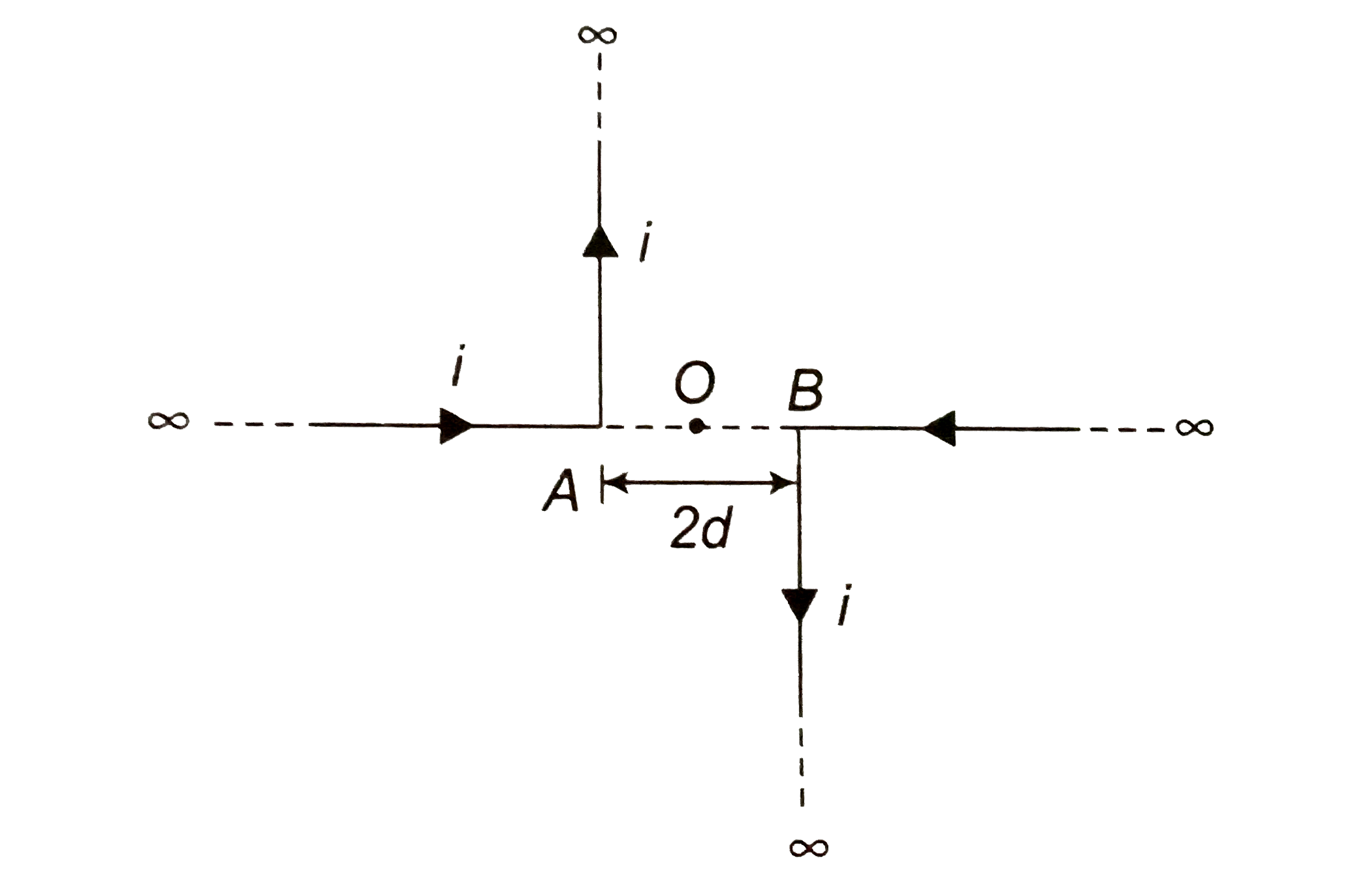 Aμ0i2πd,⊗Bμ0iπd,⊙C2μ0iπd,⊗D4μ0iπd,⊗
Aμ0i2πd,⊗Bμ0iπd,⊙C2μ0iπd,⊗D4μ0iπd,⊗In the loop shown, the magnetic induction at the point O
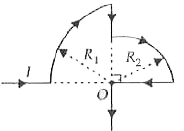 Aμ0I8(R1−R2R1R2)Bμ0I8(R1+R2R1R2)Cμ0I8(R1R2R1+R2)Dzero
Aμ0I8(R1−R2R1R2)Bμ0I8(R1+R2R1R2)Cμ0I8(R1R2R1+R2)Dzero
A loop ABCD has current I = 10 A , as shown in the figure . AD and BC are circular arcs with centre at O, for both . The magnetic field at point O is

View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
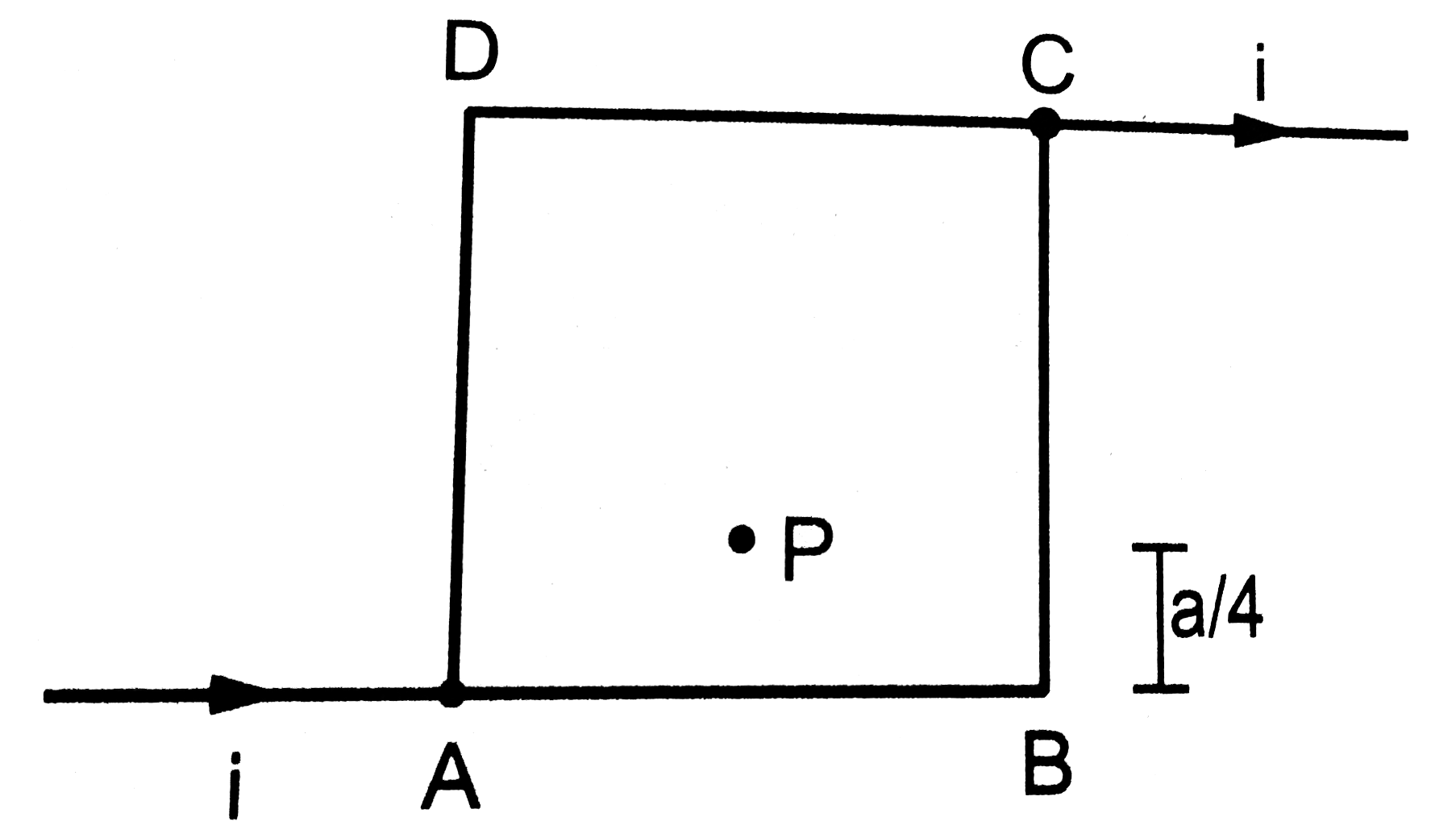
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.

View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionIn the loop shown, the magnetic induction at the point 'o' is

View Solution