If the uniform acceleration near the surface of the earth is about 9.8 m/sec2. for a free-fall, what Is the velocity at the end of 2 seconds of fall (neglect friction) ?
14.6 m/sec
17.0 m/sec
19.6 m/sec
9.8 m/sec.
The correct Answer is:C
At a uniform acceleration of 9.8 m/sec2 the body goes from 0.98 m/sec. in the first second and from 9.8 m/sec to 19.6 m/sec. at the end of the 2nd second to fall
Topper's Solved these Questions
Similar Questions
If the acceleration due to gravity on the surface of the earth is 9.8m/s2, what will be the acceleration due to gravity on the surface of a planet whose mass and radius both are two times the corresponding quantities for the earth ?
View SolutionAcceleration due to gravity on the surface of the Earth is 9.8ms−2. Find its new vallue if both the radius and mass increase by 20%.
View Solution
Knowledge Check
- Question 1 - Select One
A body falls from rest, its velocity at the end of first second is (g=32ft/sec)
A16ft/secB32ft/secC64ft/secD24ft/sec - Question 2 - Select One
The orbital velocity for an earth satellite near the surface of the earth is 8 km/sec. If the radius of the orbit is 4 times the radius of the earth, its orbital velocity will be
A8 km/sB16 km/sC4 km/sD8√2km/s - Question 3 - Select One
The figure shows the speed as a function of time for an object in free fall near the surface of the earth. The object was dropped from rest in a long evacuated cylinder .
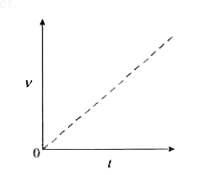
What is the speed of the object 3.0 seconds after it is dropped ?A3.0 m/sB7.7 m/sC9.8 m/sD29 m/s
The acceleration due to gravity on the surface of earth varies
View SolutionThe acceleration due to gravity on the surface of earth is 9.8ms−2.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint :Te=2π√LgeTm=2π√Lgm
T2eT2m=gmge
gm=T2eT2mgeView SolutionGiven that the radius of the Earth and acceleration due to gravity on the surface of the Earth as 6400 km and 9.8ms−2, respectively, find the acceleration due to gravity at a height of 5 km from the surface of the Earth.
View SolutionThe length of a second's pendulum on the surface of the earth, where g=9.8m/s2, is approximately equal to
View SolutionSuppose that the acceleration of a free fall at the surface of a distant planet was found to be equal to that at the surface of the earth. If the diameter of the planet were twice the diameter of the earth, then the ratio of mean density of the planet to that of the earth would be
View Solution

