using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .
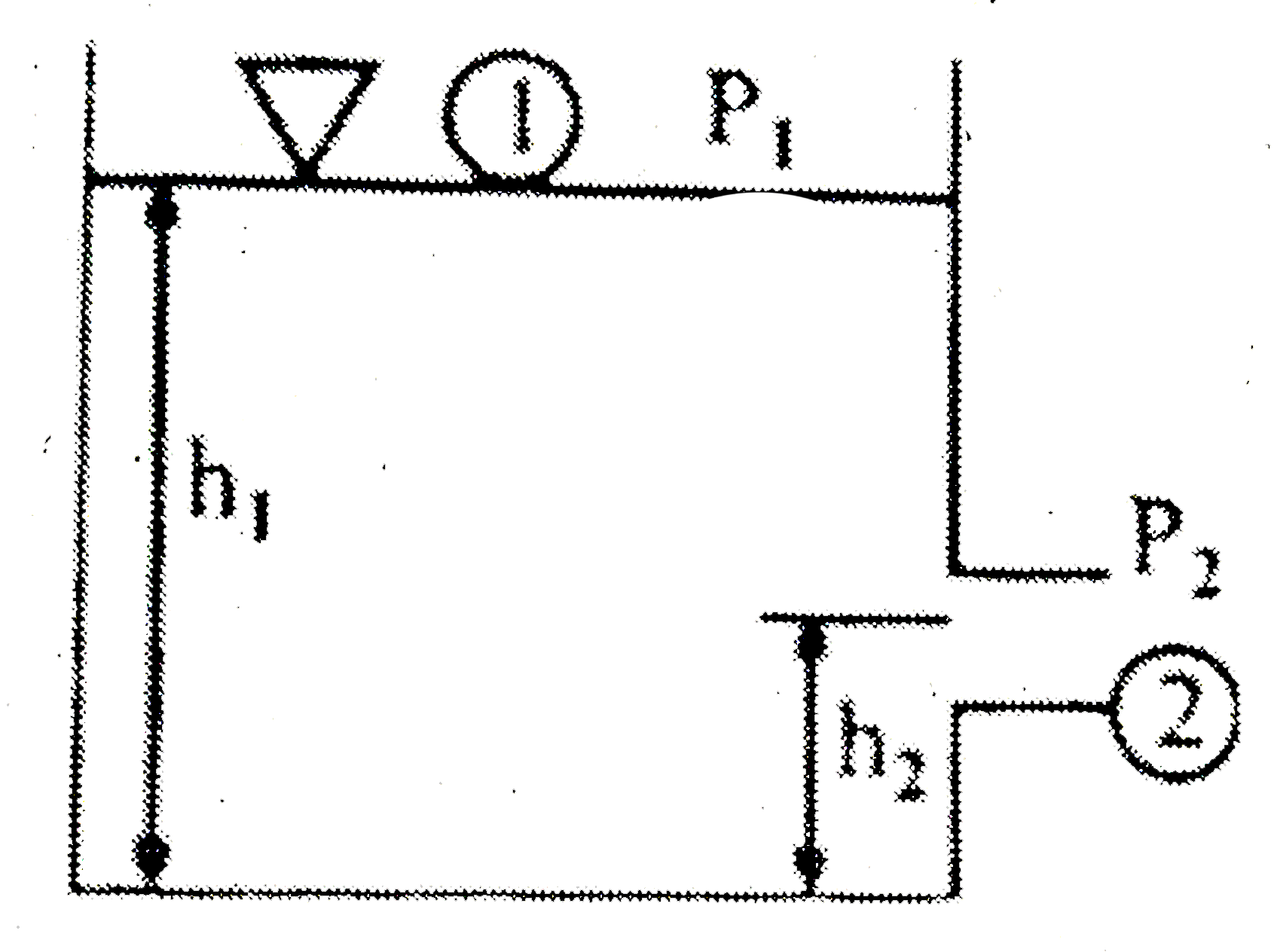
The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
The velocity of the fluid leavening point (2) is constant and can be expressed as
V2=(P1/P2)V1
V2=(P1/P2)ah
V2=[(h1−h2)(2a)]1/2
none of the above
The correct Answer is:C
h1+P1W+V212a+h2+P2W+V222a at 1 the velocity in all practical purposes =0 and P0=P2=0 then the equation above can be written as
h2+V222a=h1
V22=(h1−h2)2a
V2=[(h1−h2)(2a)]1/2
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .

The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
The value of P1 and P2 are such thatAP1=P2=0BP2 lt P1CP1>P2DP1/P2=0 - Question 2 - Select One
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .

The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
If an Identical outlet were placed at exactly the same point on the left side of the container, the velocity would beAzeroBcomputableC2V2Dnone of the above - Question 3 - Select One
The top surface of an incompressible liquid is open to the atmosphere. The pressure at a depth h1 below the surface is p1 . What is the pressure p2 at depth h2=2h1 compare with p1 ?
Ap2>2p1Bp2=2p1Cp2<2p1Dp2=p1
A horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
View SolutionAt two points on a horizontal tube of varying cross-section, the radii are 1 cm and 0.4 cm, velocities of the fluid are v1 and v2 and the pressure difference (P1−P2) between these point is 4.9 cm of water Then the value of √v22−v21 is
View SolutionFor the following concentration cell, to be spontancous Pt(H2)P1 atm. |HCl|Pt(H2)P2 atm which of the following is correct ?
View SolutionP1V1T1=P2V2T2 is -
View SolutionIn the circuit shown E,F,G and H are cells of emf 2V,1V,3V and 1V respectively and their internal resistance are 2Ω,1Ω,3Ω and 1Ω respectively.
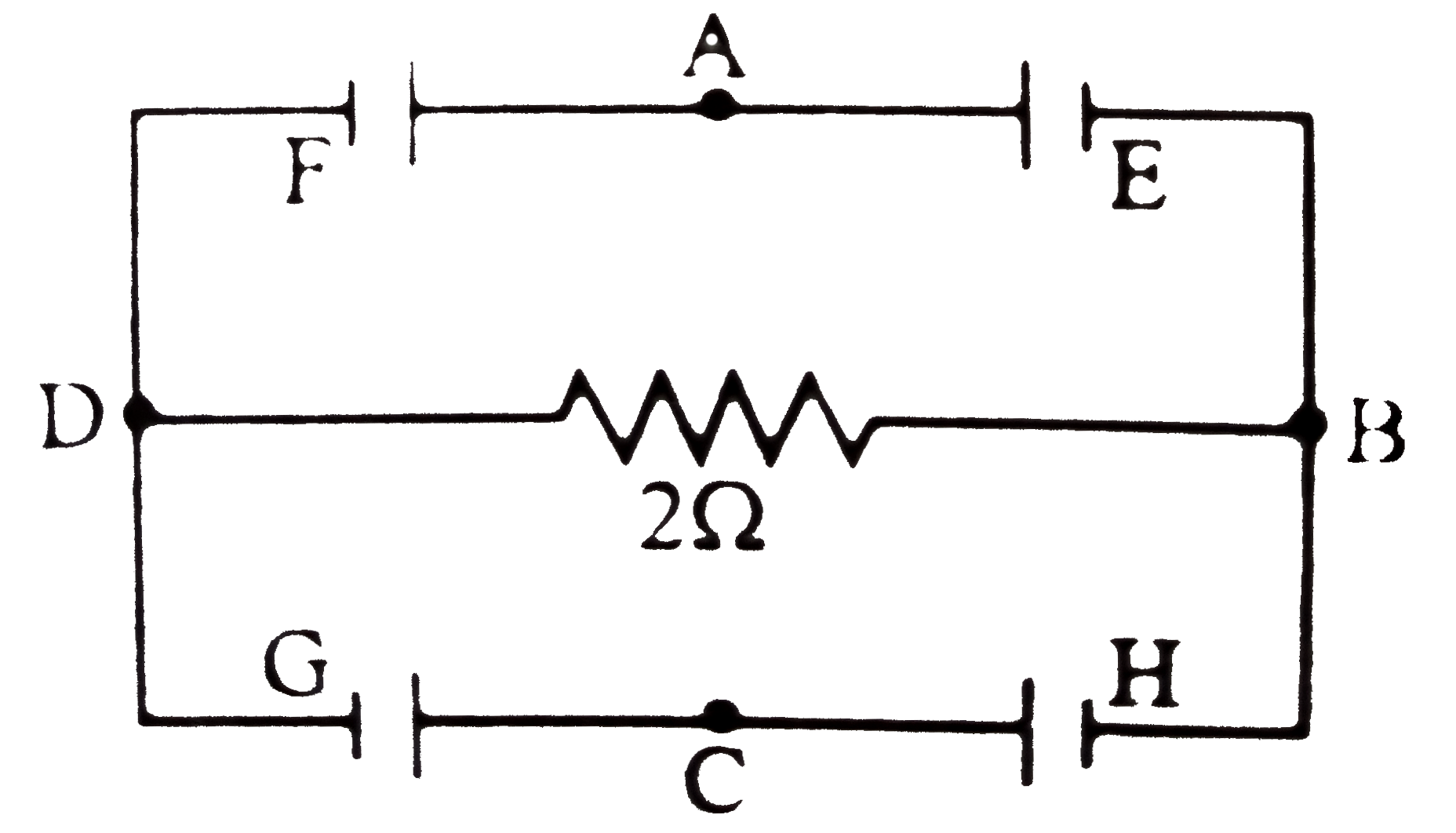 View Solution
View Solution

