If one moel of an ideal gas goes through the process A→BandB→C. Given that TA=400K, and TC=400K. If PAPB=15, then find the heat supplied to the gas.
2049.2 J
3659.2 J
2225.2 J
2659.2 J
The correct Answer is:D
ΔQ=nCVΔT+nCPΔT
=nΔT(CP−CV)
=1×8.31×(400−4005)
=8.31×4005×4
=2959.2J
Topper's Solved these Questions
Similar Questions
-
If one mole of an ideal gas goes through the process A→BandB→C. Given that TA=400K, and TC=400K. If PAPB=15, then find the heat supplied to the gas.View Solution A sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
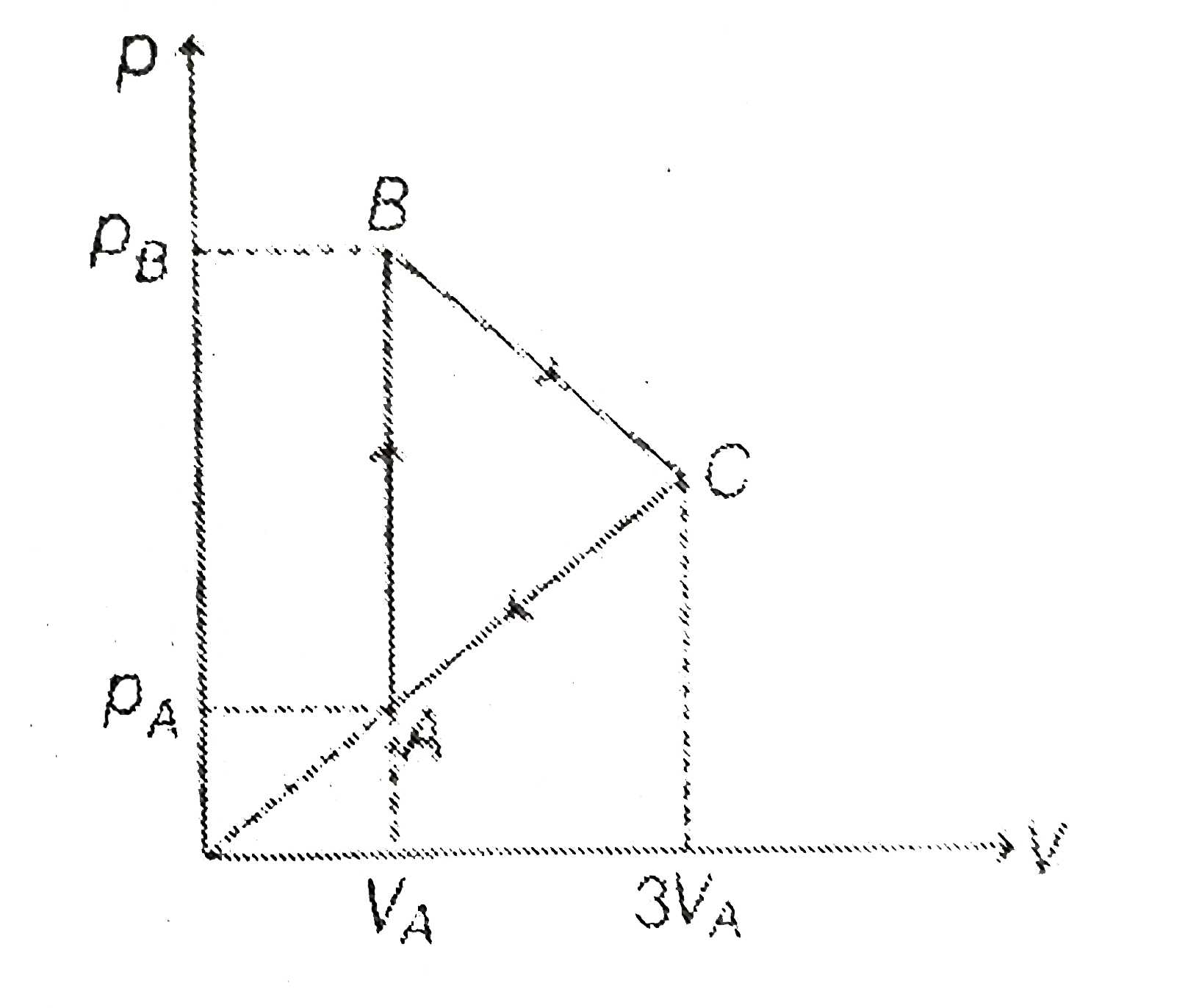
Net work done by the gas in the process isView Solution
Knowledge Check
- Question 1 - Select One
A sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
Net work done by the gas in the process isA2pAVAB4pAVAC6pAVAD8pAVA - Question 2 - Select One
A sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
What is the greastes temperature of the gas during the cyclic process ?A600 KB1200 KC2400 KDNone of these - Question 3 - Select One
One mole of an ideal monatomic gas at temperature T0 expands slowly according to the law P=kV (k is constant). If the final temperature is 4T0 then heat supplied to gas is
A2RT0B32RT0C6RT0DRT02
One mole of an ideal monatomic gas at temperature T0 expands slowly according to the law P=kV (k is constant). If the final temperature is 4T0 then heat supplied to gas is
View Solution3 moles of an ideal mono atomic gas performs a cycle as shown in fig. If gas temperature TA=400K TB=800K,TC=2400K, and TD=1200K. Then total work done by gas is
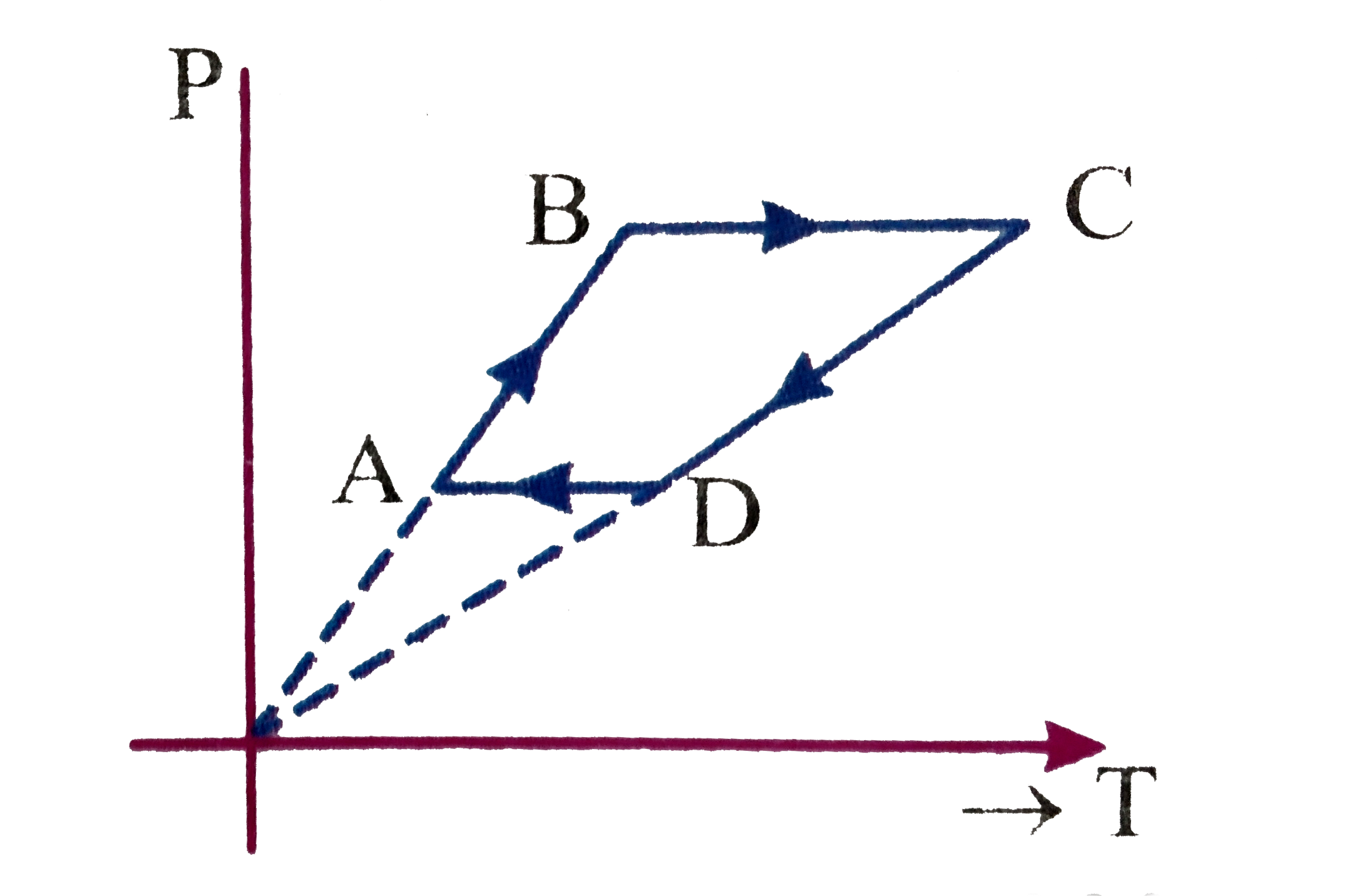
View Solution3 moles of an ideal mono atomic gas performs a cycle as shown in fig. If gas temperature TA=400K TB=800K,TC=2400K, and TD=1200K. Then total work done by gas is
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure The pressure and temperature at A, B etc are denoted by PA,PB−,TA,TB−, etc respectively
A → B adiabatic expansion
B → C cooling at constant volume
C→D adiabatic compression
D→A heating at constant volume
Given that : TA=1000 K, PB=23PA and PC=13PA
_E01_271_Q01.png)
the heat lost by the gas in process B→CView Solution3 moles of an ideal mono atomic gas performs a cycle as shown in fig. If gas temperature TA=400K TB=800K,TC=2400K, and TD=1200K. Then total work done by gas is
View Solution